Công thức Nhị thức Newton lớp 11 kèm bài tập có lời giải

1. Công thức Nhị thức Newton lớp 11:

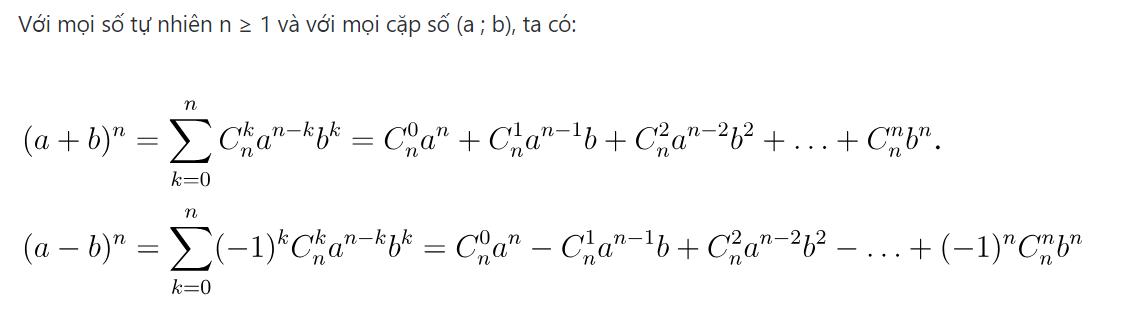
Hệ quả nhị thức Newton là một công thức quan trọng trong toán học, được sử dụng để tính các hệ số trong khai triển nhị thức của một biểu thức. Hệ quả này có một số ứng dụng quan trọng trong các lĩnh vực như xác suất, đại số và lý thuyết đồ thị.

Một ứng dụng quan trọng của hệ quả nhị thức Newton là trong lĩnh vực xác suất. Khi áp dụng công thức 2n = Cn0 + Cn1 + … + Cnn với a = b = 1, chúng ta có thể tính tổng các hệ số trong khai triển nhị thức. Điều này giúp ta phân tích xác suất của các sự kiện và hiểu rõ hơn về khả năng xảy ra của chúng trong toán học

Ngoài ra, công thức 0 = Cn0 – Cn1 + … + (–1)kCnk + … + (–1)Cnn cũng là một hệ quả thú vị của nhị thức Newton. Khi đặt a = 1 và b = –1, chúng ta có thể tính toán các hệ số trong khai triển nhị thức. Điều này giúp ta khám phá các mối quan hệ đặc biệt trong đại số và áp dụng chúng vào các vấn đề thực tế.

Với những công thức trên, chúng ta có thể dễ dàng tính toán và áp dụng vào các bài toán thực tế. Hệ quả nhị thức Newton là một công cụ hữu ích và quan trọng trong toán học, giúp chúng ta hiểu rõ hơn về cấu trúc và tính chất của các biểu thức đại số. Bên cạnh đó, việc nắm vững và áp dụng nhị thức Newton cũng mở ra nhiều cơ hội và ứng dụng trong lĩnh vực khoa học, kỹ thuật và công nghệ. Ví dụ, nhị thức Newton có thể được sử dụng để tính toán đường cong, tìm nghiệm của phương trình, và phân tích dữ liệu. Điều này giúp chúng ta áp dụng nhị thức Newton vào thực tế một cách linh hoạt và sáng tạo, tạo ra những giải pháp mới cho các vấn đề phức tạp. Nhờ vào nhị thức Newton, chúng ta có thể khám phá thêm nhiều khía cạnh mới trong lĩnh vực toán học và áp dụng chúng vào các lĩnh vực khác nhau, từ khoa học tự nhiên đến kinh tế và quản lý.

2. Tam giác Pascal trong nhị thức Newton:

n=0                                            1

n=1                                   1              1

n=2                         1                2                1

n=3             1                   3              3                 1

n=4  1                   4                6                4                1

Tam giác Pascal là một cấu trúc đặc biệt trong toán học có những tính chất thú vị.

Đầu tiên, để tạo tam giác Pascal, ta bắt đầu bằng việc ghi số 1 ở đỉnh của tam giác. Tiếp theo, ta tạo hàng thứ nhất bằng cách ghi hai số 1. Điều này có nghĩa là hàng thứ nhất của tam giác Pascal sẽ luôn là [1, 1].

Quy luật chính để tạo hàng thứ n + 1 từ hàng thứ n trong tam giác Pascal là cộng hai số liên tiếp của hàng thứ n. Kết quả của phép cộng này sẽ được viết xuống hàng dưới ở vị trí giữa hai số đó. Đồng thời, ta cũng ghi số 1 ở đầu và cuối hàng để đảm bảo tính chất đặc biệt của tam giác Pascal.

Ví dụ, nếu ta đã có hàng thứ 3 của tam giác Pascal là [1, 3, 3, 1], ta có thể tạo được hàng thứ 4 bằng cách cộng từng cặp số liên tiếp trong hàng thứ 3: 1 + 3 = 4, 3 + 3 = 6, 3 + 1 = 4. Kết quả là hàng thứ 4 của tam giác Pascal sẽ là [1, 4, 6, 4, 1].

Quy trình này có thể tiếp tục để tạo ra các hàng tiếp theo của tam giác Pascal. Mỗi hàng mới sẽ được tạo bằng cách áp dụng quy luật trên vào hàng trước đó.

Tam giác Pascal có các tính chất đặc biệt và được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như lý thuyết xác suất, đại số, và cả trong lĩnh vực lập trình. Nó cung cấp một cách tuyệt vời để biểu diễn các tổ hợp và phương trình đồng dư.

Nhận xét:

Trong quá trình khai triển biểu thức Niu tơn (a + b)n, chúng ta có thể nhận thấy các tính chất sau:

Biểu thức có tổng cộng n + 1 số hạng, đại diện cho tất cả các cách kết hợp các hạng tử a và b trong biểu thức ban đầu.

Số mũ của a giảm từ n đến 0 trong mỗi số hạng, trong khi số mũ của b tăng từ 0 đến n. Điều này cho phép chúng ta khai triển và biểu diễn tất cả các mức độ của a và b trong biểu thức.

Tổng của các số mũ của a và b trong mỗi số hạng đều bằng n, cho phép chúng ta định rõ quan hệ giữa các hạng tử a và b trong biểu thức.

Các hệ số trong biểu thức có tính đối xứng, điều này có nghĩa là các hệ số ở cùng vị trí từ hai đầu của khai triển là giống nhau. Ví dụ: hệ số đầu tiên và hệ số cuối cùng, hệ số thứ hai và hệ số thứ hai cuối cùng, và cứ tiếp tục như vậy.

Có một quan hệ đặc biệt giữa hai hệ số liên tiếp trong khai triển, được gọi là quan hệ Pascal. Quan hệ này cho phép chúng ta tính toán các hệ số trong khai triển chỉ thông qua hệ số trước đó và không cần tính toán lại từ đầu.

Số hạng tổng quát thứ k + 1 trong khai triển có thể được tính toán bằng cách sử dụng công thức tổng quát. Công thức này dựa trên các hệ số và mũ của a và b, và cho phép chúng ta tính toán giá trị của một số hạng cụ thể trong khai triển.

Như vậy, việc hiểu và áp dụng các tính chất trên sẽ giúp chúng ta dễ dàng khai triển và tính toán các biểu thức Niu tơn (a + b)n.

Các dạng toán nhị thức Newton:

– Dạng toán 1. Tìm hệ số hoặc số hạng trong khai triển nhị thức Newton.

Trong dạng toán này, chúng ta sẽ tìm hệ số hoặc số hạng trong khai triển nhị thức Newton. Phương pháp giải bao gồm sử dụng công thức tổng quát và áp dụng các quy tắc toán học để tính toán kết quả. Để hiểu rõ hơn về cách giải, chúng ta sẽ xem xét một số bài tập mẫu và bài tập tương tự. Cuối cùng, để rèn luyện kỹ năng, học sinh cũng có thể thực hiện các bài tập về nhà.

– Dạng toán 2. Chứng minh hoặc tính tổng.

Trong dạng toán này, chúng ta sẽ chứng minh hoặc tính tổng. Phương pháp giải sẽ dựa trên các quy tắc toán học và sử dụng các bước logic để đưa ra lời giải hoặc tính toán kết quả. Chúng ta cũng sẽ xem xét một số bài tập mẫu và bài tập tương tự để hiểu rõ hơn về cách giải. Học sinh cũng có thể thực hiện các bài tập về nhà để nắm vững kiến thức.

– Dạng toán 3. Tìm hệ số hoặc số hạng dạng có điều kiện (kết hợp giữa dạng toán 1 và dạng toán 2).

Dạng toán này kết hợp giữa dạng toán 1 và dạng toán 2. Chúng ta sẽ tìm hệ số hoặc số hạng dạng có điều kiện trong khai triển nhị thức Newton. Phương pháp giải sẽ bao gồm áp dụng công thức tổng quát, sử dụng các quy tắc toán học và logic để tính toán kết quả. Chúng ta cũng sẽ xem xét một số bài tập mẫu và bài tập tương tự để nắm bắt cách giải. Để rèn luyện kỹ năng, học sinh cũng có thể thực hiện các bài tập về nhà giúp nắm vững kiến thức.

Trong mỗi dạng toán, chúng ta đã cung cấp tóm tắt phương pháp giải, một số bài tập mẫu và bài tập tương tự, cũng như các bài tập về nhà giúp học sinh tự rèn luyện kỹ năng và nắm vững kiến thức.

3. Nhị thức Newton lớp 11 kèm bài tập có lời giải:

Câu 1: Gọi Tk là số hạng thứ k trong khai triển (x3+2y2)13 mà tổng số mũ của x và y trong số hạng đó bằng 32. Hệ số của Tk bằng?

A.198620 B.186284 C.219648 D.2012864

Hướng dẫn giải :

Đáp án : C

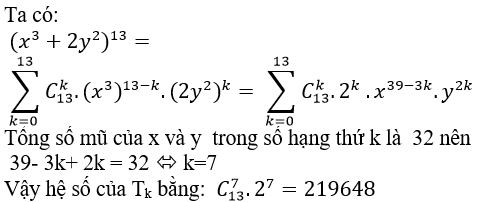
Câu 2: Gọi a3n- 3 là hệ số của số hạng chứa x3n- 3 trong khai triển (x2+1)n.(x+2)n. Tìm n sao cho a3n- 3 = 26n?

A.n=4 B.n=5 C.n=6 D.n=7

Lời giải:

Đáp án : B

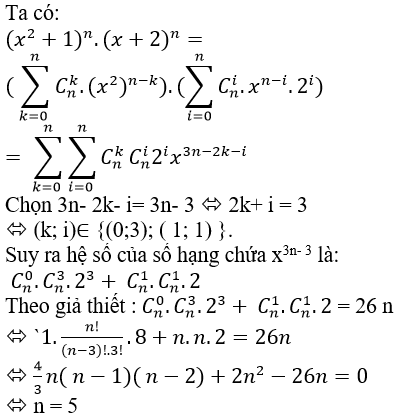
Câu 3: Cho kahi triển x(x+1)n + 2( x+1)n= a0+ a1x+ a2.x2+ …+ an+1xn+1 với n là số tự nhiên và n≥2. Tìm n; biết rằng a2 – 7n; n.an ; an-2 theo thứ tự đó lập thành một cấp số cộng.

A.n= 6 B.n= 8 C.n= 10 D.n= 12

Lời giải:

Đáp án : C

Ta có

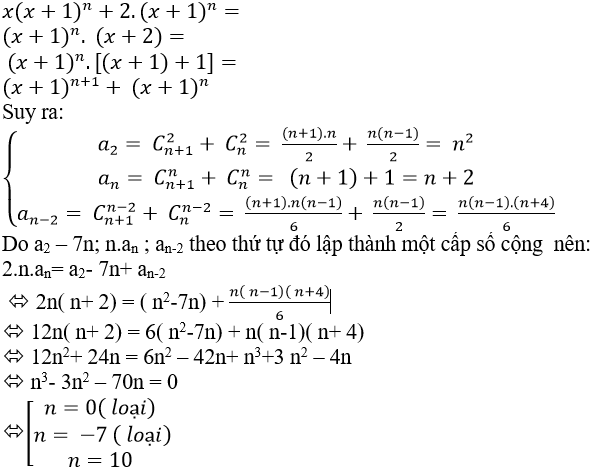
Vậy n=10