Công thức Hệ thức lượng trong tam giác vuông Toán lớp 9

1. Các hệ thức lượng giác trong tam giác vuông:

1.1. Hệ thức liên quan về cạnh và đường cao:

Trong đề bài ta có một hình tam giác vuông ABC và dữ liệu được cho sẵn là vuông tại A cùng với AH là đường cao của tam giác này, khi đó ta có các hệ thức mà các bạn học sinh lớp 9 cần nhớ liên quan sau đây:

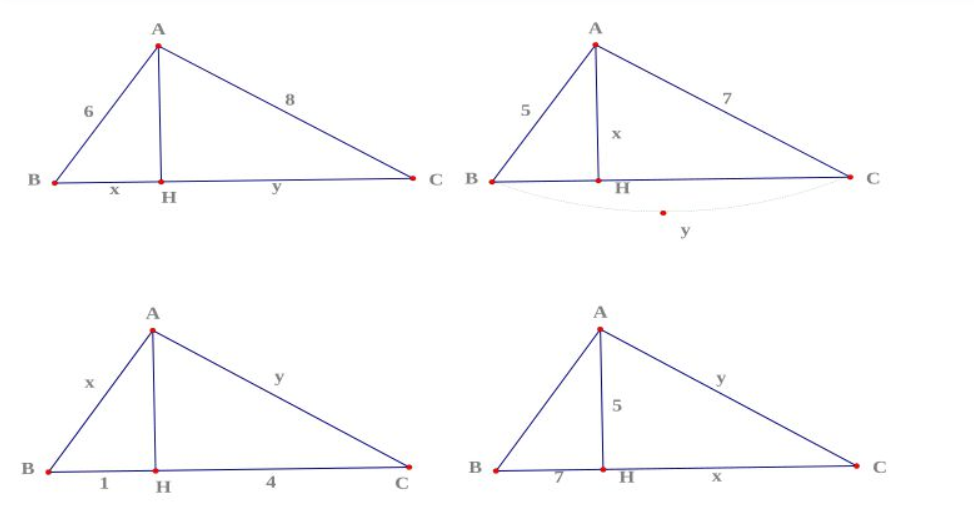
Các hệ thức liên quan đến hệ thức lượng trong tam giác vuông và tam giác thường

AB bình = BH x BC

AC bình = CH x BC

AH bình = BH x CH

AB x AC = AH x BC

1/đường cao bình = 1/AB bình x 1/AC bình

Cạnh huyền trong tam giác bình phương bằng tổng bình phương của hai cạnh góc vuông trong tam giác đó.

1.2. Tỉ số lượng giác của góc nhọn:

Một số kiến thức quan trọng có liên quan đến các công thức lượng giác và hệ thức lượng tam giác vuông mà chúng tôi chuẩn bị nhắc tới như sau:

a) Định nghĩa về tỉ số lượng giác

Sin alpha = Đối / Huyền

Cos alpha = Kề / Huyền

Tan alpha = Đối / Kề

Cot alpha = Kề / Đối

b) Định lý về tỷ số lượng giác

Trong một tam giác vuông được cho sẵn , nếu hai góc phụ nhau thì có công thức áp dụng giải bài tập như: sin góc này bằng cos góc kia, tan góc này bằng cot góc kia và ngược lại.

c) Các so sánh cần nhớ của hệ số lượng giác

Cho 2 góc alpha và belta được nhận diện là 2 góc nhọn của một tam giác vuông tức là hai góc có tổng số đo là 90 độ và alpha bé hơn belta thì:

Sin alpha < Sin beta và đồng thời Tan alpha < Tan beta

Cos alpha > Cos beta và tương tự ta có Cot alpha > Cot beta

Sin alpha < Tan alpha và bên cạnh đó thì Cos alpha < Cot alpha

2. 4 Định lý lượng giác trong tam giác vuông:

Các định lý lượng giác trong tam giác vuông được chúng tôi tổng hợp để các bạn học dinh dễ học và dễ hình dung hơn:

Định lí 1

Trong một tam giác vuông bất kì, ta luôn có bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền trong tam giác đó và hình chiếu tương ứng của cạnh góc vuông đó ứng với cạnh huyền.

b² = ab’ ; c² = ac’

Định lí 2

Trong một tam giác vuông bất kì, bình phương đường cao ứng với cạnh huyền sẽ bằng tích hai hình chiếu của hai cạnh góc vuông tương ứng đó trên cạnh huyền.

h² = b’c’

Định lí 3

Trong một tam giác vuông cho sẵn, tích hai cạnh góc vuông bằng tích của cạnh huyền tương ứng và đường cao nối từ đỉnh góc vuông của tam giác đó.

ah = bc

Định lí 4

Trong một tam giác vuông được cho sẵn, nghịch đảo của bình phương đường cao ứng với cạnh huyền trong tam giác đó sẽ bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông tương ứng.

3. Tỉ số lượng giác của góc nhọn:

Nếu α cho trước là một góc nhọn bất kỳ thì:

0 < sinα <1

0< cosα <1, tanα > 0

cotα > 0, sin2α + cos2α = 1

tanα.cotα = 1; tanα = sinα.cosα

cotα = cosα.sinα

1 + tan2α = 1cos2α

1 + cot2α = 1sin2α

4. Hướng dẫn một số dạng bài tập hệ thức lượng trong tam giác:

Dưới đây là một số dạng bài tập tiêu biểu đại diện cho việc áp dụng các hệ thức lượng trong tam giác vuông lớp 9 được nêu ra ở trên:

* Chứng minh các hệ thức và tính giá trị của biểu thức 

Phương pháp giải:

Vận dụng các phương pháp chứng minh đẳng thức: biến đổi để hai vế bằng nhau, từ giả thiết ban đầu dẫn đến đẳng thức đã được công nhận là đúng,… Vận dụng các định lý trong tam giác vuông, tam giác thường, các hệ thức lượng giác.

* Tính toán các đại lượng

Phương pháp giải:

Vận dụng tính sin, cos, trung tuyến, diện tích và mối liên hệ giữa các đại lượng cần tính, các tam giác đặc biệt.

* Chứng minh tam giác 

Phương pháp giải:

Vận dụng các hệ thức lượng giác, định lý, công thức diện tích, đường trung tuyến, các bất phương trình và hằng số cơ bản.

* Các bài toán thực tế về giải tam giác

Phương pháp giải cụ thể:

Giải tam giác là tìm số đo các cạnh và góc còn lại trong tam giác khi biết giả thiết, vận dụng các hệ thức lượng, định lý, công thức diện tích, đường trung tuyến,… Bài toán thực tế giải được. bằng cách quay trở lại bài toán tam giác để xác định số đo cần thiết

5. Tổng hợp bài tập vận dụng và hướng dẫn giải chi tiết nhất:

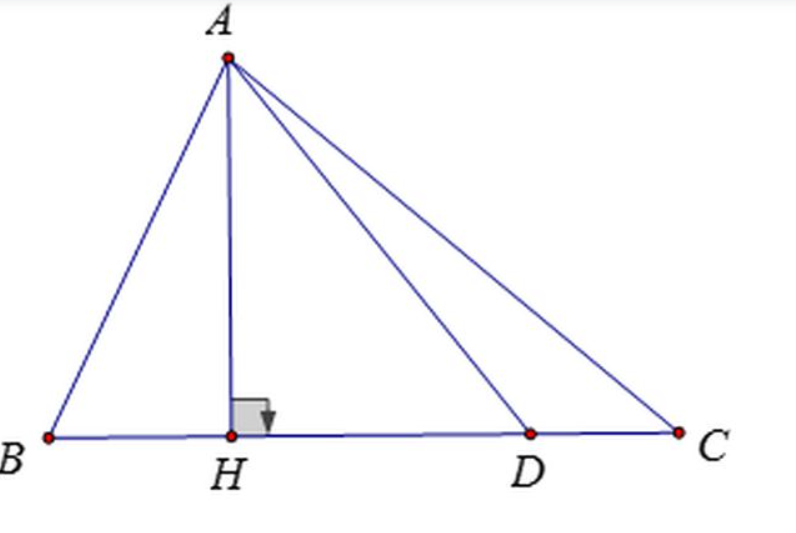
Bài 1: Cho tam giác vuông ABC vuông tại A, có đường cao AH của tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài lần lượt là 3 và 4. Vận dụng các quan hệ đã học ở phần trên để có thể tính các cạnh. góc vuông của tam giác ABC như hình minh hoạ bên trên.

Lời giải: Ở bài toán này trước tiên ta cần xét các yếu tố dữ kiện mà bài toán đã cho. Lưu ý các góc vuông tương ứng và xác định đâu là cạnh huyền và góc nào là góc vuông. Sau đó quan sát các cạnh cần tính là thuộc cạnh nào của tam giác vuông. Sau đó, xem xét các dữ liệu có sẵn và chọn hệ số tương ứng để áp dụng. Đối với bài toán này ta sử dụng hệ thức giữa cạnh góc vuông và hình chiếu để tính toán theo yêu cầu của bài toán.

Bài 2: Cho tam giác ABC vuông tại A có cạnh góc vuông kề với góc 60 độ của tam giác vuông này bằng 3. Sử dụng bảng lượng giác các góc đặc biệt để tìm cạnh huyền và cạnh góc vuông còn lại (Lưu ý bạn cần phải làm tròn số vừa tính đến chữ số thập phân thứ tư nhé).

Lời giải: Một tam giác ABC vuông cân tại A thì trong 2 góc còn lại, góc lớn hơn là 60 độ và ngược lại là 30 độ. Khi đó cạnh đối diện của góc 60 độ đó bằng 3. Sau đó ta áp dụng từng công thức đã học trong bảng lượng giác để tính cạnh huyền và cạnh góc vuông còn lại.

Bài 3: Vận dụng kiến ​​thức đã học viết các tỉ số lượng giác sau thành các tỉ số lượng giác của các góc nhỏ hơn 45 độ, gồm sin 60 độ, cos 75 độ, sin52 độ 30′, cot 82 độ, tan 80 độ.

Lời giải: Đây là dạng toán cơ bản khi học về tỉ số lượng giác của góc nhọn. Trong bài toán này ta chỉ cần vận dụng tính chất lượng giác của hai góc đối đỉnh trong một tam giác vuông. Sau đó thay đổi nó thành giá trị của góc tương ứng. 

Bài 4: Tìm x, y trong hình vẽ:

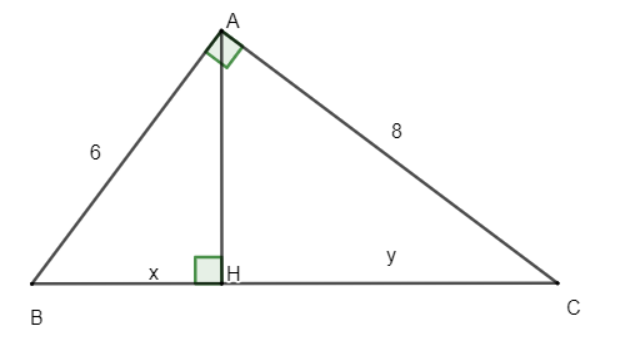
Lời giải:

Áp dụng định lý Py – ta – go cho tam giác vuông ABC ta có:

AB² + AC² = BC²

⇔ 6² + 8² = BC²

⇔ BC² = 100²

⇔ BC = 10

Với AH là đường cao, áp dụng hệ thức lượng cho tam giác vuông ABC ta có:

AB² = BH.BC

⇔ 6² = BH.10

⇔ 36 = BH.10

⇔ BH = 36 : 10

⇔ BH = 3,6

Tương tự ta có:

AC² = CH.BC

⇔ 8² = CH.10

⇔ 64 = CH.10

⇔ CH = 64 : 10

⇔ CH = 6,4

Bài 5: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB : AC = 3: 4 và BC=15. Tính BH, CH.

Lời giải:

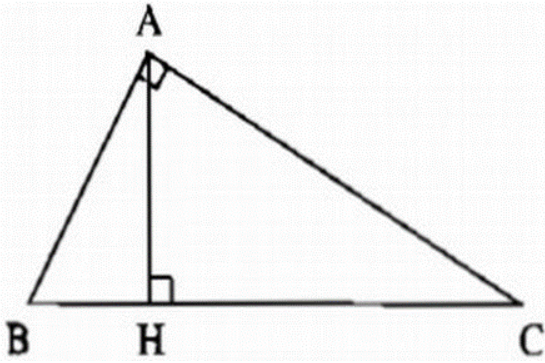
Ta có: AB : AC = 3 : 4

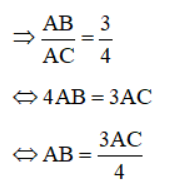
Áp dụng định lý Py – ta – go cho tam giác ABC vuông tại A ta có:

AB² + AC² = BC²

Thay BC = 15; 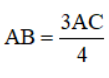 ta có:

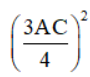+ AC² = 15²

⇔ AC² + AC² = 225

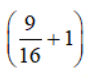⇔ AC² = 225

⇔ AC² = 225

⇔ AC² = 225 :

⇔ AC² = 144

⇔ AC = 12

Áp dụng hệ thức lượng cho tam giác ABC vuông tại A đường cao AH ta có:

AB² = BH.BC

⇔ 12²= CH.15

⇔ CH = 144 : 15

⇔ CH = 9,6

=> BH = BC – CH = 15 – 9,6 = 5,4

Bài 6: Cho tam giác CDE nhọn, đường cao CH. Gọi M, N theo thứ tự là hình chiếu của H lên CD, CE. Chứng minh:

a) CD.CM = CE.CN

b) Tam giác CMN đồng dạng với tam giác CED

Lời giải:

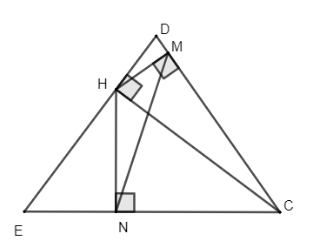
a) Áp dụng hệ thức lượng cho tam giác DCH vuông tại H ta có:

CH² = CM.CD (1)

Áp dụng hệ thức lượng cho tam giác CEH vuông tại H ta có:

CH² = CN.CE (2)

Từ (1) và (2)

=> CH² = CN.CE = CM.CD

=> CN.CE = CM.CD

b) Ta có:

CN.CE = CM.CD

Xét tam giác CMN và tam giác CED ta có:

 chung

(chứng minh trên)

=> ΔCMN ∼ ΔCED (c – g – c)

THAM KHẢO THÊM:

• che-do-chinh-sach-voi-dang-vien-30-40-50-nam-tuoi-dang-1.jpg-1.jpg
• Trục căn thức ở mẫu của biểu thức (Bài tập Toán lớp 9)
• Axit Silixic là gì? Tính chất hóa học và ứng dụng của H2SiO3?