Trong toán học, delta và delta phẩy là một trong những phương trình bậc hai rất hay và khó. Bài viết dưới đây sẽ hướng dẫn cách tính delta và delta phẩy phương trình bậc 2 nhanh, chính xác.
Mục lục bài viết
1. Công thức cách tính delta:
Trong toán học, delta (đôi khi được ký hiệu là Δ) là một khái niệm quan trọng liên quan đến các phương trình bậc hai. Delta được sử dụng để xác định số lượng và tính chất của các nghiệm của phương trình. Cụ thể, delta xuất hiện trong Công thức nghiệm của phương trình bậc hai.
Phương trình bậc hai có dạng chung là , với a, b, và c là các hằng số và x là biến số. Công thức nghiệm cho phương trình bậc hai được biểu diễn như sau:
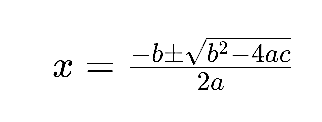 Ở đây, ± biểu thị hai giá trị khác nhau của x có thể được tìm thấy. Phần bên trong căn bậc hai, b^, chính là delta. Delta đóng vai trò quan trọng trong việc xác định tính chất của các nghiệm của phương trình. Khi , phương trình có hai nghiệm phân biệt; khi Δ=0, phương trình có một nghiệm kép; và khi Δ<0, phương trình không có nghiệm thực.
Ở đây, ± biểu thị hai giá trị khác nhau của x có thể được tìm thấy. Phần bên trong căn bậc hai, b^, chính là delta. Delta đóng vai trò quan trọng trong việc xác định tính chất của các nghiệm của phương trình. Khi , phương trình có hai nghiệm phân biệt; khi Δ=0, phương trình có một nghiệm kép; và khi Δ<0, phương trình không có nghiệm thực.
Ngoài ra, delta còn có ứng dụng rộng rãi trong các lĩnh vực khác nhau như vật lý, kỹ thuật, kinh tế học, và nhiều lĩnh vực khác. Trong mỗi ngữ cảnh, delta mang lại những thông tin quan trọng về sự biến đổi, sự chênh lệch hay tính chất đặc biệt của một hệ thống hay vấn đề cụ thể.
Tóm lại, delta là một khái niệm toán học quan trọng và có ứng dụng rộng rãi, đặc biệt trong việc giải và nghiên cứu các phương trình bậc hai và nhiều lĩnh vực khác của khoa học và kỹ thuật.
2. Công thức cách tính delta phẩy:
Delta phẩy (Δ′) là một khái niệm quan trọng trong toán học và được sử dụng rộng rãi trong việc nghiên cứu các hàm số bậc hai. Nó cung cấp thông tin về tính chất và đặc điểm cực đại hoặc cực tiểu của hàm số.
Công thức để tính delta phẩy là:
Δ′=
Ở đây, a, b, và c lần lượt là các hệ số của phương trình bậc hai . Delta phẩy được tạo ra từ phần bên trong căn bậc hai của công thức nghiệm của phương trình bậc hai.
Việc tính toán delta phẩy mang lại thông tin quan trọng về hình dạng của đồ thị hàm số. Khi , hàm số có điểm chót và có cực đại hoặc cực tiểu tùy thuộc vào dấu của a. Khi , hàm số cũng có điểm chót nhưng không có cực đại hoặc cực tiểu. Trong trường hợp , hàm số không có điểm chót.
Ứng dụng của delta phẩy không chỉ giới hạn trong toán học mà còn lan rộng vào nhiều lĩnh vực khác nhau như vật lý, kinh tế học, thống kê, và các ngành công nghiệp liên quan đến phân tích dữ liệu.
Tóm lại, delta phẩy là một khái niệm quan trọng trong toán học và có ứng dụng rộng rãi trong việc nghiên cứu và phân tích các hàm số bậc hai và nhiều lĩnh vực khác của khoa học và kỹ thuật.
3. Công thức cách tính phương trình bậc 2:
Phương trình bậc hai là một dạng phương trình toán học quan trọng, thường có dạng , trong đó a, b, và c là các hằng số và x là biến số. Để giải phương trình bậc hai, chúng ta thường sử dụng Công thức nghiệm.
Công thức nghiệm cho phương trình bậc hai được biểu diễn như sau:
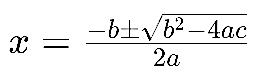 Ở đây, dấu ±± biểu thị hai giá trị khác nhau của x có thể được tìm thấy. Phần bên trong căn bậc hai, , được gọi là delta (Δ). Delta đóng vai trò quan trọng trong việc xác định số lượng và tính chất của các nghiệm của phương trình. Khi , phương trình có hai nghiệm phân biệt; khi , phương trình có một nghiệm kép; và khi , phương trình không có nghiệm thực.
Ở đây, dấu ±± biểu thị hai giá trị khác nhau của x có thể được tìm thấy. Phần bên trong căn bậc hai, , được gọi là delta (Δ). Delta đóng vai trò quan trọng trong việc xác định số lượng và tính chất của các nghiệm của phương trình. Khi , phương trình có hai nghiệm phân biệt; khi , phương trình có một nghiệm kép; và khi , phương trình không có nghiệm thực.
Công thức này đã có ảnh hưởng sâu rộng trong nhiều lĩnh vực của toán học và khoa học tự nhiên. Nó được ứng dụng trong cả vật lý, kỹ thuật, thống kê, và nhiều lĩnh vực khác. Phương trình bậc hai là một công cụ mạnh mẽ giúp giải quyết nhiều vấn đề thực tế.
Đáng chú ý, kiến thức về cách giải phương trình bậc hai không chỉ quan trọng trong học tập mà còn trong đời sống hàng ngày, đặc biệt đối với những người theo hướng nghiên cứu hoặc công việc yêu cầu sự sử dụng toán học một cách sâu rộng. Công thức nghiệm của phương trình bậc hai đóng vai trò quan trọng trong việc xác định và giải quyết các vấn đề có tính chất toán học trong thực tế.
4. Bài tập vận dụng:
Bài 1: Giải các phương trình sau:


a, Tìm m để phương trình có nghiệm x = 1
b, Tìm m để phương trình có nghiệm kép
c, Tìm m để phương trình có hai nghiệm phân biệt
Nhận xét: đây là một dạng toán giúp các bạn học sinh ôn tập được kiến thức về cách tính công thức nghiệm của phương trình bậc hai cũng như ghi nhớ được các trường hợp nghiệm của phương trình bậc hai.
Lời giải:
a, x = 1 là nghiệm của phương trình (1). Suy ra thay x = 1 vào phương trình (1) có:


Lời giải:
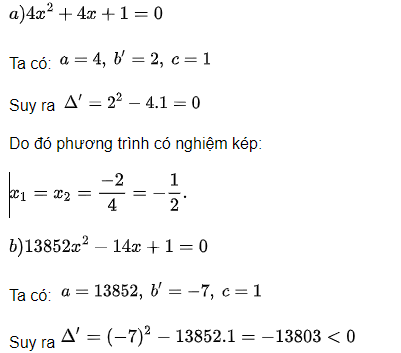
Do đó phương trình vô nghiệm.
Bài 4: Giải các phương trình dưới đây:
a, x2 – 5x + 4 = 0
(Học sinh tính được ∆ và nhận thấy ∆ > 0 nên phương trình đã cho có hai nghiệm phân biệt)
Ta có: ∆ = b2 – 4ac = (-5)2 – 4.1.4 = 25 – 16 = 9 > 0
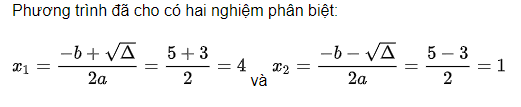
Vậy tập nghiệm của phương trình là: S = {1; 4}
b, 6x2 + x + 5 = 0
(Học sinh tính được ∆ và nhận thấy ∆ < 0 nên phương trình đã cho vô nghiệm)
Ta có: ∆ = b2 – 4ac = 12 – 4.6.5 = 1 – 120 = – 119 < 0
Phương trình đã cho vô nghiệm.
Vậy phương trình vô nghiệm.
c, 16x2 – 40x + 25 = 0
(Học sinh tính được ∆ hoặc tính công thức nghiệm thu gọn ∆’ và nhận thấy ∆’ = 0 nên phương trình đã cho có nghiệm kép)
Ta có: ∆’ = b’2 – ac = (-20)2 – 16.25 = 400 – 400 = 0
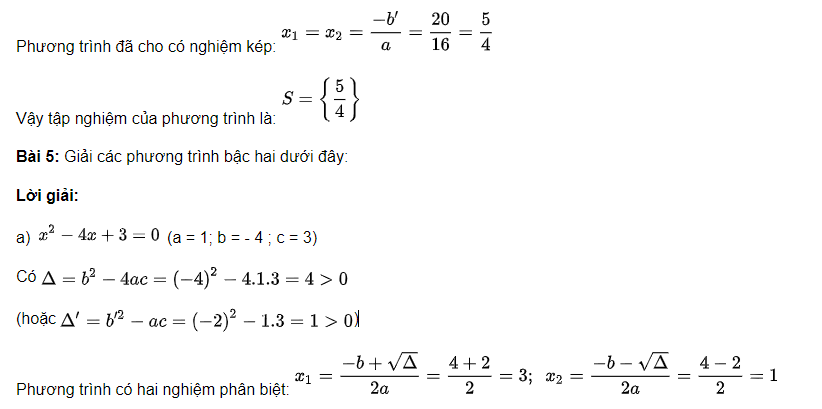
Vậy tập nghiệm của phương trình là S = {1; 3}
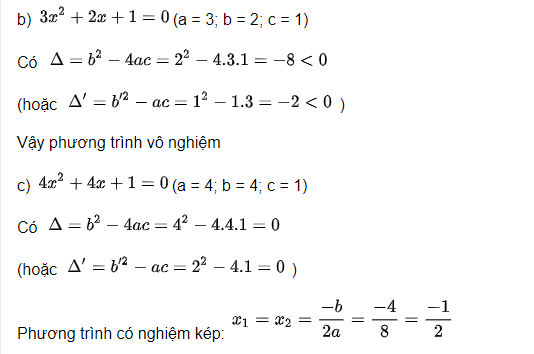


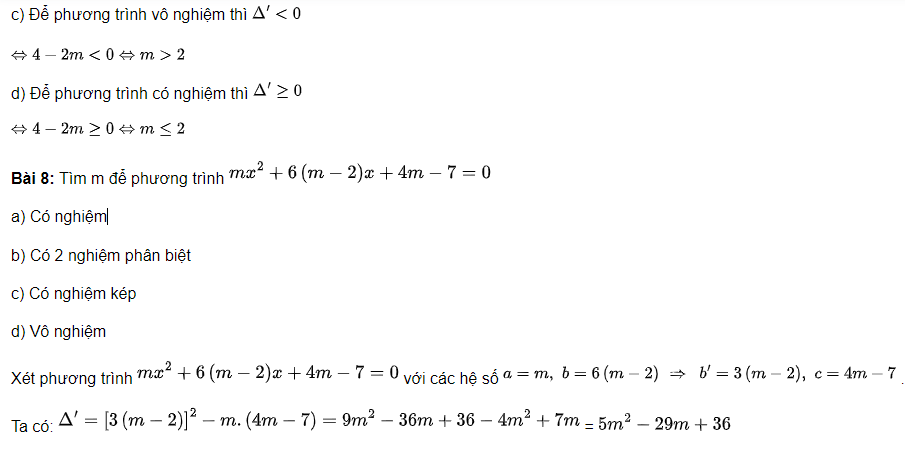
a) Để phương trình có nghiệm thì:





