Toán lớp 4 trang 76: Phép chia - Chia một tổng cho một số với đáp án và hướng dẫn giải chi tiết. Lời giải bài tập Toán 4 này giúp học sinh biết tính chất một tổng chia cho một số, cách vận dụng bài tập về tính chất chia một tổng cho một số.
Mục lục bài viết
1. Bài tập Chia một tổng cho một số Toán lớp 4 trang 76:
Bài 1 Toán lớp 4 trang 76:
Tính các biểu thức sau
a) (15 + 35) : 5; (80 + 4) : 4
b) 18 : 6 + 24 : 6; 60 : 3 + 9 : 3.
* Tính bằng hai cách (theo mẫu)
Mẫu: 12 : 4 + 20 : 4 = ?
– Cách 1 : 12 : 4 + 20 : 4 = 3 + 5 = 8
– Cách 2 : 12 : 4 + 20 : 4 = (12 + 20) : 4
= 32 : 4 = 8.
* Phương pháp giải:
Khi chia một tổng cho một số, nếu các số hạng của tổng đều chia hết cho số chia thì ta có thể chia từng số hạng cho số chia, rồi cộng các kết quả tìm được với nhau.
* Lời giải chi tiết:
a) (15 + 35) : 5 = ?
– Cách 1: (15 + 35) : 5 = 50 : 5 = 10
– Cách 2: (15 + 35) : 5 = 15 : 5 + 35 : 5 = 3 + 7 = 10
(80 + 4) : 4 = ?
– Cách 1: (80 + 4) : 4 = 84 : 4 = 21
– Cách 2: 80 : 4 + 4 : 4 = 20 + 1 = 21
b) 18 : 6 + 24 : 6 = ?
– Cách 1 : 18 : 6 + 24 : 6 = 3 + 4 = 7
– Cách 2 : 18 : 6 + 24 : 6 = (18 + 24) : 6 = 42 : 6 = 7
60 : 3 + 9 : 3 = ?
– Cách 1: 60 : 3 + 9 : 3 = 20 + 3 = 23
– Cách 2: 60 : 3 + 9 : 3 = (60 + 9) : 3 = 69 : 3 = 23
Bài 2 Toán lớp 4 trang 76:
Tính các biểu thức sau
a) (27 – 18) : 3
b) (64 – 32) : 8.
* Tính bằng hai cách theo mẫu:
Mẫu: (35 – 21) : 7 = ?
– Cách 1: (35 – 21) : 7 = 14 : 7 = 2
– Cách 2: (35 – 21) : 7 = 35 : 7 – 21 : 7 = 5 – 3 = 2
* Phương pháp giải:
Tính tương tự như ví dụ mẫu:
– Cách 1: Tính trong ngoặc trước, ngoài ngoặc sau
– Cách 2: Áp dụng công thức (a – b) : c = a : c – b : c
* Lời giải chi tiết:
a) (27 – 18) : 3 =?
– Cách 1 : (27 – 18) : 3 = 9 : 3 = 3
– Cách 2 : (27 – 18) : 3 = 27 : 3 – 18 : 3 = 9 – 6 = 3
b) (64 – 32) : 8 = ?
– Cách 1 : (64 – 32) : 8 = 32 : 8 = 4
– Cách 2 : (64 – 32) : 8 = 64 : 8 – 32 : 8 = 8 – 4 = 4
Bài 3 Toán lớp 4 trang 76:
Lớp 4A có 32 học sinh chia thành các nhóm, mỗi nhóm có 4 học sinh. Lớp 4B có 28 học sinh cũng chia thành các nhóm, mỗi nhóm có 4 học sinh. Hỏi tất cả có bao nhiêu nhóm?
* Phương pháp giải:
– Cách 1:
+ Tính số nhóm của lớp 4A. Ta lấy số học sinh của lớp 4A chia cho số học sinh cho 1 nhóm.
+ Tính số nhóm của lớp 4B. Ta lấy số học sinh của lớp 4B chia cho số học sinh cho 1 nhóm.
+ Tính tổng số nhóm = số nhóm của lớp 4A + số nhóm của lớp 4B
– Cách 2:
+ Tính tổng số học sinh của 2 lớp
+ Tính tổng số nhóm. Ta lấy tổng số học sinh của hai lớp chia cho số học sinh trong một nhóm.
* Lời giải chi tiết:
Tóm tắt
32 học sinh chia mỗi nhóm: 4 học sinh
28 học sinh chia mỗi nhóm: 4 học sinh
Có tất cả: ? nhóm
– Cách 1:
Số nhóm học sinh của lớp 4A là:
32 : 4 = 8 (nhóm)
Số nhóm học sinh của lớp 4B là:
28 : 4 = 7 (nhóm)
Số nhóm học sinh của cả hai lớp 4A và 4B là:
8 + 7 = 15
Đáp số: 15 nhóm.
– Cách 2:
Hai lớp có tất cả số học sinh là:
32 + 28 = 60 (học sinh)
Số nhóm học sinh của cả hai lớp 4A và 4B là:
60 : 4 = 15 (nhóm)
Đáp số: 15 nhóm.
2. Lý thuyết phép chia Toán lớp 4:
2.1. Phép chia là gì?
Phép chia là phép tính chia một số thành một số phần bằng nhau.
* Ví dụ:
20 : 4 = ?
Nếu bạn lấy 20 phần và đặt chúng thành bốn nhóm có kích thước bằng nhau thì sẽ có 5 phần trong mỗi nhóm. Cho nên câu trả lời là 5.
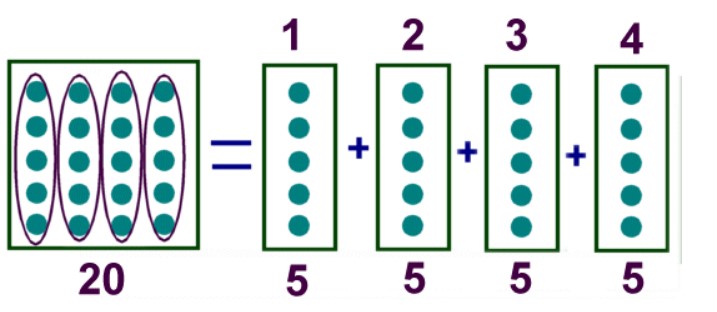
Đáp án: 20 : 4 = 5
2.2. Dấu hiệu của phép chia:
Có một số dấu hiệu mà chúng ta có thể sử dụng để chỉ ra phép chia. Dấu hiệu phổ biến nhất là kí tự ÷, nhưng dấu gạch chéo ngược / đôi khi cũng được sử dụng. Hoặc chúng ta có thể viết một số lên trên một số khác với một dòng giữa chúng. Đây cũng được gọi là phân số.
Dấu hiệu ví dụ cho “a chia cho b”:

2.3. Số bị chia, Số chia và Thương số:
Mỗi phần của phép chia đều có tên gọi của nó, đó là số bị chia, số chia và thương số.
Số bị chia – Số đang chia
Số chia – Số đang chia cho
Thương số – Đáp án của phép chia
Số bị chia ÷ Số chia = Thương số
* Ví dụ:
Trong bài toán 20 ÷ 4 = 5
Số bị chia = 20
Số chia = 4
Thương số = 5
2.4. Trường hợp đặc biệt của phép chia:
Có ba trường hợp đặc biệt cần xem xét khi thực hiện phép chia.
* Chia cho 1: Khi chia một số cho 1, câu trả lời chính là số ban đầu. Nói cách khác, nếu số chia là 1 thì thương số bằng số bị chia.
Ví dụ:
20 ÷ 1 = 20
14,7 ÷ 1 = 14,7
* Chia cho 0: Bạn không thể chia một số cho 0. Đáp án cho phép chia này là không xác định.
* Số bị chia bằng số chia: Nếu số bị chia và số chia bằng nhau (chứ không phải 0), thì câu trả lời luôn là 1.
* Ví dụ:
20 ÷ 20 = 1
14.7 ÷ 14.7 = 1
2.5. Số dư:
Nếu đáp án cho một bài toán chia không phải là một số nguyên, thì “phần còn lại” được gọi là số dư.
Ví dụ, phép chia 20 cho 3, bạn sẽ phát hiện ra rằng 20 không chia hết được cho 3. Các số gần nhất với 20 mà có thể chia đều cho 3 là 18 và 21. Lúc này bạn chọn số gần nhất chia được cho 3 mà nhỏ hơn 20. Đó là 18.
18 chia cho 3 = 6, nhưng vẫn còn dư lại 2.
20 -18 = 2.
20 ÷ 3 = 6 dư 2
* Ví dụ:
12 ÷ 5 = 2 dư 2
23 ÷ 4 = 5 dư 3
18 ÷ 7 = 2 dư 4
2.6. Phép chia là nghịch đảo của phép nhân:
Một cách khác để nghĩ về phép chia đó là nghịch đảo của phép nhân.
* Ví dụ:
20 ÷ 4 = 5
Bạn có thể làm ngược lại, thay thế dấu = bằng dấu x và dấu ÷ bằng dấu =, ta được:
5 x 4 = 20
* Ví dụ:
12 ÷ 4 = 3
→ 3 x 4 = 12
21 ÷ 3 = 7
→ 7 x 3 = 21
3. Bài tập vận dụng liên quan:
Bài 1: Tính và so sánh giá trị biểu thức
a) (35 +21) : 7 và 35 : 7 + 21 : 7
b) (24 + 48) : 6 và 24 : 6 + 48 : 6
c) (45 + 50) : 5 và 45 : 5 + 50 : 5
d) (78 + 54) : 2 và 78 : 2 + 54 : 2
Lời giải chi tiết:
a) Ta có: (35 +21) : 7 = 56 : 7 = 8
Ta có: 35 : 7 + 21 : 7 = 5 + 3 = 8
Vậy (35 +21) : 7 = 35 : 7 + 21 : 7
b) Ta có: (24 + 48) : 6 = 72 : 6 = 12
Ta có 24 : 6 + 48 : 6 = 4 + 8 = 12
Vậy (24 + 48) : 6 = 24 : 6 + 48 : 6
c) Ta có: (45 + 50) : 5 = 19
Ta có 45 : 5 + 50 : 5 = 9 + 10 = 19
Vậy (45 + 50) : 5 = 45 : 5 + 50 : 5
d) Ta có: (78 + 54) : 2 = 132 : 2 = 66
Ta có 78 : 2 + 54 : 2 = 39 + 27 = 66
Vậy (78 + 54) : 2 = 78 : 2 + 54 : 2
Bài 2: Tính biểu thức sau bằng hai cách
a) (56 + 58) : 2
b) (90 + 27) : 3
c) (60 – 30) : 6
d) (88 – 32) : 8
Lời giải chi tiết:
a) (56 + 58) : 2
– Cách 1: (56 + 58) : 2 = 56 : 2 + 58 : 2 = 28 + 29 = 57
– Cách 2: (56 + 58) : 2 = 114 : 2 = 57
b) (90 + 27) : 3
– Cách 1: (90 + 27) : 3 = 90 : 3 + 27 : 3 = 30 + 9 = 39
– Cách 2: (90 + 27) : 3 = 117 : 3 = 39
c) (60 – 30) : 6
– Cách 1: (60 – 30) : 6 = 60 : 6 – 30 : 6 = 10 – 5 = 5
– Cách 2: (60 – 30) : 6 = 30 : 6 = 5
d) (88 – 32) : 8
– Cách 1: (88 – 32) : 8 = 88 : 8 – 32 : 8 = 11 – 4 = 7
– Cách 2: (88 – 32) : 8 = 56 : 8 = 7
Bài 3: Vườn cây ăn quả nhà Lan có 42 cây nhãn, mỗi hàng có 6 cây. 54 cây ổi mỗi hàng cũng có 6 cây. Hỏi tất cả có bao nhiêu hàng cây? (Giải bằng 2 cách).
Lời giải chi tiết:
– Cách 1:
Tổng số cây trong vườn nhà Lan là:
42 + 54 = 96 (cây)
Mỗi hàng có 6 cây, có số hàng là:
96 : 6 = 16 (hàng)
Vậy vườn nhà Lan có 16 hàng
– Cách 2:
42 cây nhãn được chia thành số hàng là
42 : 6 = 7 (hàng)
54 cây ổi được chia thành số hàng là
54 : 6 = 9 (hàng)
Tổng số hàng cây trong vườn nhà Lan là
7 + 9 = 16 (hàng)
Vậy có tổng 16 hàng cây ăn quả trong vườn nhà Lan.




