Câu trắc nghiệm hệ thức lượng trong tam giác có đáp án dưới đây là câu trả lời cho câu hỏi trên kèm theo một vài câu hỏi khác có liên quan nhằm giúp bạn đọc có thể hình dung rõ hơn về câu hỏi cũng như giúp bạn đọc có thêm nhiều kiến thức mới hay và bổ ích, mời bạn đọc đón xem bài viết dưới đây chúc các bạn học tập thật tốt.
Mục lục bài viết
1. Câu trắc nghiệm hệ thức lượng trong tam giác có đáp án:
Câu 1: Cho tam giác ABC có AB = 4, AC = 6, góc A = 120o. Độ dài cạnh BC là:
A. √19 B. 2√19 C. 3√19 D. 2√7
Hướng dẫn giải
Đáp án B

Câu 2: Cho tam giác ABC có AB = 4, AC = 5, BC = 6. Giá trị cos A bằng
A. 0,125 B. 0,25 C. 0,5 D. 0,0125
Hướng dẫn giải
Đáp án A
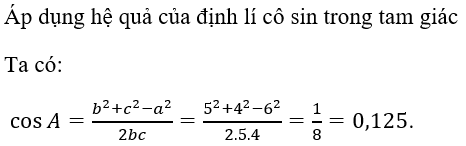
Câu 3: Cho tam giác ABC có a = 3, b = 5, c = 6. Giá trị của mc bằng
A. √2 B. 2√2 C. 3 D. √10
Hướng dẫn giải
Đáp án D
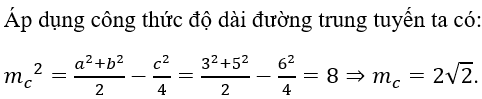
Câu 4: Cho tam giác ABC. Khẳng định nào sau đây là đúng?
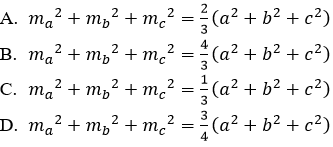
Hướng dẫn giải
Đáp án D
Cách 1.
Sử dụng công thức trung tuyến, ta có:
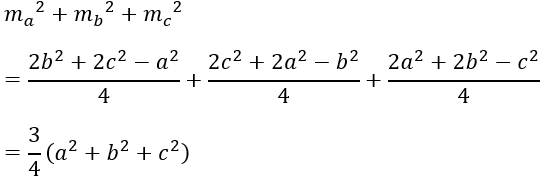
Cách 2.
(Chỉ sử dụng trong tình huống thi trắc nghiệm có bốn phương án như trên).
Nếu đẳng thức đúng với mọt tam giác thì đúng với tam giác đều. Tam giác đều cạnh a có độ dài đường trung tuyến:
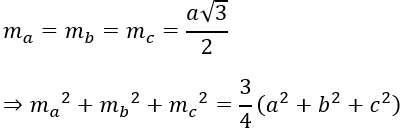
Trong đó a = b = c.
Các khẳng định A, B, C không đúng trong trường hợp đặc biệt nên không thể là phương án đúng.
Câu 5: Cho tam giác ABC là tam giác đều cạnh a. Bán kính đường tròn ngoại tiếp tam giác ABC bằng.
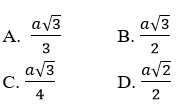
Hướng dẫn giải
Đáp án A

Câu 6: Cho tam giác ABC có AB = 10, AC = 12, góc A = 150o.Diện tích của tam giác ABC bằng
A. 60 B. 30 C.60√3 D. 30√3
Hướng dẫn giải
Đáp án B
![]()
Câu 7: Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Bán kính đường tròn nội tiếp của tam giác ABC bằng
A. 4 B. 3 C. 2 D. 1
Hướng dẫn giải
Đáp án D

Câu 8: Cho tam giác ABC có AC = 6, BC = 8. ha ,hb lần lượt là độ dài các đường cao đi qua các đỉnh A, B. Tỉ số ha/hb bằng

Hướng dẫn giải
Đáp án A
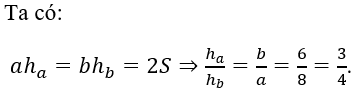
Câu 9: Cho tam giác ABC có a = 5, b = 6, c = 7. Diện tích của tam giác ABC bằng
A. 12√6 B. 3√6 C. 6√6 D. 9√6
Hướng dẫn giải
Đáp án C

Câu 10: Cho tam giác ABC có a = 3, b = 5, c = 6. Bán kính đường trong nội tiếp của tam giác bằng
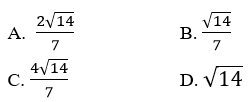
Hướng dẫn giải
Đáp án A

Câu 11: Cho tam giác ABC có a = 5, b = 12, c = 13. Bán kính đường tròn ngoại tiếp R của tam giác bằng
A. 13 B. 26 C. 6,5 D. 7,5
Hướng dẫn giải
Đáp án C

Câu 12: Cho tam giác ABC có a = 2, b=2√2 ,góc C = 135o. Độ dài cạnh c là
A. 8 B. 4√2 C. 2√2 D. 2√5
Hướng dẫn giải
Đáp án D
Áp dụng định lí cosin trong tam giác ta có:
c2=22+(2√2)2-2.2.2√2.cos135o=4+8-2.2.2√2.(-1/√2)=20,c=2√5
Câu 13: Cho tam giác ABC có a=√3,b=4,c=2√3. Giá trị của cos B là:
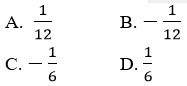
Hướng dẫn giải
Đáp án B
Áp dụng hệ quả định lí cosin trong tam giác ta có:
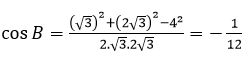
Câu 14: Cho tam giác ABC có a = 2, b = 3, c=√19. Số đo của góc C là
A. 135o B. 150o C. 60o D. 120o
Hướng dẫn giải
Đáp án D
Áp dụng hệ quả định lí cosin trong tam giác ta có:
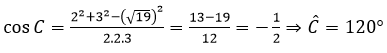
Câu 15: Cho tam giác ABC có a2 =b2 + c2 – bc. Số đo của góc A là
A. 135o B. 150o C. 60o D. 120o
Hướng dẫn giải
Đáp án C
Ta có: a2 = b2 + c2 – bc nên b2 + c2 – a2 = bc
Áp dụng hệ quả định lí cosin trong tam giác ta có:
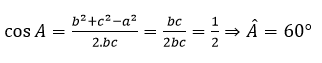
Câu 16: Cho tam giác ABC có a2 =b2 + c2 + √2.bc. Số đo của góc A là
A. 135o B. 45o C. 120o D. 150o
Hướng dẫn giải
Đáp án A
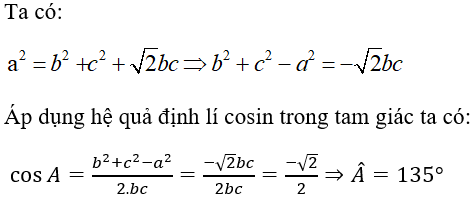
Câu 17: Cho tam giác ABC. Khẳng định nào sau đây là đúng?
A. Nếu b2 +c2 > a2 thì góc A > 90o
B. Nếu b2 +c2 = a2 thì góc A ≠ 90o
C. Nếu b2 +c2 ≠ a2 thì tam giác ABC không phải là tam giác vuông
D. Nếu b2 +c2 > a2 thì góc A > 90o
Hướng dẫn giải
Đáp án D
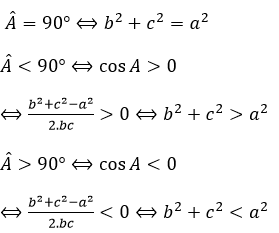
Câu 18: Cho tam giác ABC có a = 3 cm, b = 4 cm, c = 5 cm. Tam giác ABC là
A. Tam giác nhọn
B. Tam giác tù
C. Tam giác vuông
D. Tam giác đều
Hướng dẫn giải
Đáp án C
Ta có: a2 + b2 = c2 nên tam giác ABC là tam giác vuông.
Câu 19: Cho tam giác ABC có a = 8 cm, b = 9 cm, c = 10 cm. Tam giác ABC là
A. Tam giác nhọn
B. Tam giác tù
C. Tam giác vuông
D. Tam giác đều
Hướng dẫn giải
Đáp án A
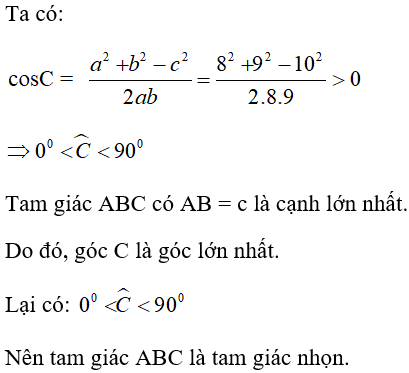
Câu 20: Cho tam giác ABC có a = 6 cm, b = 7 cm, c = 10 cm. Tam giác ABC là
A. Tam giác nhọn
B. Tam giác tù
C. Tam giác vuông
D. Tam giác đều
Hướng dẫn giải
Đáp án B
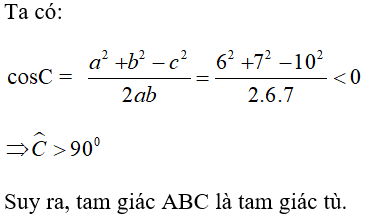
2. Hệ thức lượng trong tam giác:
Hệ thức lượng trong tam giác là một công cụ mạnh mẽ giúp chúng ta khám phá và hiểu rõ hơn về mối quan hệ giữa các cạnh và góc trong tam giác. Một trong những công thức quan trọng nhất là Định lý Sin. Định lý này kết nối độ dài của một cạnh với sin của góc đối diện, thông qua đường kính của đường tròn ngoại tiếp tam giác. Điều này cung cấp cho chúng ta một công cụ hữu ích để tính toán độ dài các cạnh và góc trong tam giác.
Ngoài ra, Định lý Cosin cũng đóng vai trò quan trọng trong việc giải các bài toán tam giác. Định lý này cho phép chúng ta tính toán độ dài của cạnh thứ ba khi đã biết hai cạnh và góc xen giữa, hoặc tính toán góc khi đã biết ba cạnh của tam giác. Điều này cung cấp cho chúng ta một phương pháp linh hoạt để giải quyết nhiều vấn đề khác nhau liên quan đến tam giác.
Bằng cách hiểu và áp dụng các hệ thức này, chúng ta có thể giải quyết các vấn đề phức tạp hơn trong hình học và toán học. Hơn nữa, khả năng sử dụng các công cụ này cũng mở ra cánh cửa cho việc áp dụng chúng trong các lĩnh vực khác như vật lý, kỹ thuật, và khoa học máy tính. Điều này làm cho hệ thức lượng trong tam giác trở thành một phần không thể thiếu của trí tuệ toán học và ứng dụng của nó trong thế giới thực.
3. Áp dụng hệ thức lượng ngoài thực tế:
Hệ thức lượng trong tam giác không chỉ là một phần của bộ công cụ toán học, mà còn là một công cụ quan trọng và linh hoạt trong nhiều lĩnh vực thực tiễn khác nhau. Tính linh hoạt của nó cho phép chúng ta giải quyết nhiều vấn đề phức tạp một cách hiệu quả, từ thiết kế kỹ thuật đến đo đạc địa lý và nhiều lĩnh vực khác.
Một trong những ứng dụng phổ biến nhất của hệ thức lượng trong tam giác là trong việc tính toán các đoạn cạnh và góc của tam giác khi biết các thông tin đầu vào như độ dài của các cạnh và góc giữa chúng. Với thông tin này, chúng ta có thể sử dụng các định lý Cosin và Sin để tính toán các giá trị còn thiếu. Ví dụ, khi biết một cạnh và hai góc, ta có thể sử dụng định lý Cosin để tính toán các cạnh còn lại hoặc định lý Sin để tính toán góc còn thiếu. Tương tự, khi biết hai cạnh và góc xen giữa, chúng ta cũng có thể sử dụng các định lý này để tính toán các giá trị khác.
Ngoài ra, khi biết độ dài của ba cạnh của tam giác, ta có thể sử dụng định lý Cosin để tính toán góc hoặc các cạnh còn lại. Điều này cho phép chúng ta giải quyết các vấn đề phức tạp hơn trong các lĩnh vực như thiết kế kỹ thuật, địa lý, v.v.
Ứng dụng của hệ thức lượng trong tam giác không chỉ giới hạn ở các vấn đề cụ thể mà còn mở ra cánh cửa cho việc áp dụng chúng trong nhiều tình huống thực tế khác nhau. Chẳng hạn, trong công nghệ và công nghiệp, việc tính toán các góc và đoạn cạnh của các cấu trúc kỹ thuật là cần thiết để đảm bảo tính chính xác và an toàn của các công trình xây dựng. Trong địa lý và đo đạc địa lý, việc sử dụng hệ thức lượng giúp dự đoán và mô hình hóa địa hình một cách chính xác, đặc biệt trong việc xác định độ dốc của một khu vực hoặc tính toán khoảng cách giữa các điểm.
Với những ứng dụng đa dạng như vậy, hệ thức lượng trong tam giác không chỉ là một công cụ toán học trừu tượng mà còn là một phần quan trọng của cuộc sống hàng ngày, đóng vai trò quan trọng trong việc giải quyết các vấn đề thực tế và phát triển công nghệ.
THAM KHẢO THÊM:




