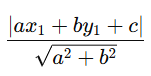Cách tính khoảng cách từ một điểm đến một đường thẳng

1. Cách tính khoảng cách từ một điểm đến một đường thẳng:

Phương pháp tính khoảng cách từ một điểm đến một đường thẳng là một phần quan trọng trong hình học phổ thông và được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau như máy hình, máy tính đồ họa, và thiết kế đồng thời.

Để hiểu rõ hơn về phương pháp này, chúng ta cần tập trung vào quy trình cụ thể của nó. Đầu tiên, để tính khoảng cách từ một điểm M đến đường thẳng Δ, ta cần xác định hình chiếu H của điểm M lên đường thẳng Δ. Có hai cách thực hiện điều này:

Cách 1: Trong mặt phẳng chứa điểm M và đường thẳng Δ, vẽ đoạn thẳng MH vuông góc với Δ. Khoảng cách từ M đến Δ sẽ bằng độ dài của đoạn MH.

Cách 2: Dựng một mặt phẳng (α) vuông góc với Δ và đi qua điểm M. Khoảng cách từ M đến Δ sẽ bằng chiều cao của tam giác MHΔ trên mặt phẳng (α).

Sau khi xác định được điểm H, tiếp theo là sử dụng công thức tính khoảng cách từ một điểm đến một đường thẳng. Cho đường thẳng Δ có phương trình ax + by + c = 0 và điểm M có tọa độ (x1, y1), công thức tính khoảng cách là:

d(M,Δ)= ​

Ở đây,  là giá trị tuyệt đối của $ax1+by1+c$, và ​ là căn bậc hai của tổng bình phương của hai hệ số a và b của đường thẳng.

Điều này nói lên rằng, để tính khoảng cách từ một điểm đến một đường thẳng, chúng ta cần biết phương trình của đường thẳng và tọa độ của điểm đó. Quy trình này không chỉ là một ứng dụng hữu ích của toán học trong thực tế mà còn là một công cụ quan trọng giúp chúng ta hiểu rõ hơn về không gian và tương tác giữa các đối tượng hình học.

Ví dụ 1: Khoảng cách từ điểm M( 1; -1) đến đường thẳng ( a) : 3x – 4y – 21 = 0 là:

A. 1    B. 2    C. 4/5  D. 14/5

Hướng dẫn giải

Khoảng cách từ điểm M đến đường thẳng ( a) là:

d(M;a) =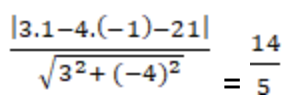  

Chọn D.

Ví dụ 2: Khoảng cách từ điểm O đến đường thẳng d: x/6+y/8= 1 là:

A. 4,8    B. 1/10   C. 1    D. 6

Hướng dẫn giải

Đường thẳng d:  x/6+y/8= 1 ⇔ 8x + 6y – 48 = 0

⇒ Khoảng cách từ điểm O đến đường thẳng d là :

d( O; d) = 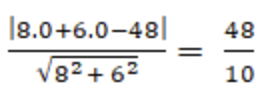 = 4,8

Chọn A.

Ví dụ 3. Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng (d): 8x + 6y + 100 = 0. Bán kính R của đường tròn (C) bằng:

A. R = 4    B. R = 6    C. R = 8    D. R = 10

Lời giải

Do đường thẳng d tiếp xúc với đường tròn ( C) nên khoảng cách từ tâm đường tròn đến đường thẳng d chính là bán kính R của đường tròn

⇒ R= d(O; d) =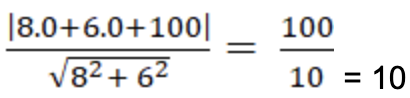

Chọn D.

Ví dụ 5 . Khoảng cách từ điểm M( -1; 1) đến đường thẳng d: 3x – 4y + 5 = 0 bằng:

Lời giải

Khoảng cách từ điểm M đến đường thẳng d là:

d( M; d) =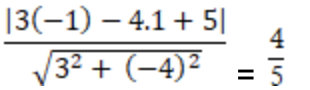  

Chọn A.

2. Bài tập Cách tính khoảng cách từ một điểm đến một đường thẳng:

I. Trắc nghiệm

Câu 1. Khoảng cách từ điểm M( 1; -1) đến đường thẳng ( a) : 3x – 4y – 21 = 0 là:

A. 1

B. 2

C. 4/5

D. 14/5

Câu 2. Khoảng cách từ điểm O đến đường thẳng d:x/6 + y/8 = 1 là:

A. 4,8

B. 1/10

C. 1

D. 6

Câu 3. Khoảng cách từ điểm M(2; 0) đến đường thẳng {x = 1 + 3t; y = 2 + 4t}

A. 2

B. 2/5

C. 10/

D. /2

Câu 4. Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng (d): 8x + 6y + 100 = 0. Bán kính R của đường tròn (C) bằng:

A. R = 4

B. R = 6

C. R = 8

D. R = 10

Câu 5. Khoảng cách từ điểm M( -1; 1) đến đường thẳng d: 3x – 4y + 5 = 0 bằng:

A. 2/5

B. 1

C. 4/5

D. 4/25

Câu 6. Khoảng cách từ giao điểm của hai đường thẳng (a): x – 3y + 4 = 0 và (b): 2x + 3y – 1 = 0 đến đường thẳng ∆: 3x + y + 16 = 0 bằng:

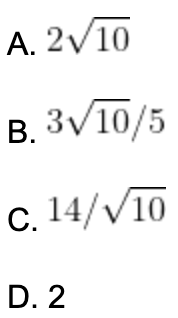
Câu 7. Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A( 1; 2) ; B(0; 3) và C(4; 0) . Chiều cao của tam giác kẻ từ đỉnh A bằng:

A. 1/5

B. 3

C. 1/25

D. 3/5

Câu 8. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(3; -4); B(1; 5) và C(3;1) . Tính diện tích tam giác ABC.

A. 10

B. 5

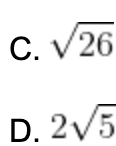
Câu 9. Hai cạnh của hình chữ nhật nằm trên hai đường thẳng d1 : 4x – 3y + 5 = 0 và d2: 3x + 4y – 5 = 0, đỉnh A

( 2; 1). Diện tích của hình chữ nhật là:

A. 1.

B. 2

C. 3

D. 4

Câu 10. Cho hình chóp tam giác S.ABC với SA vuông góc với (ABC) và SA=3a. Diện tích tam giác ABC bằng 2a2, BC=a . Khoảng cách từ S đến BC bằng bao nhiêu?

A. 2a.

B. 4a

C. 3a

D. 5a

II. Tự luận

Câu 1. Cho một đường thẳng có phương trình có dạng d’: 2x + 2y + 5 = 0. Tính khoảng cách từ M (2; 3) tới đường thẳng d’.

Câu 2. Cho một đường thẳng có phương trình có dạng d: – x + 3y + 1 = 0. Hãy tính khoảng cách từ Q (2; 1) tới đường thẳng d.

Câu 3. Tính khoảng cách từ giao điểm của hai đường thẳng (d) : x + y – 2 = 0 và ( ∆) : 2x + 3y – 5 = 0 đến đường thẳng (d’) : 3x – 4y + 11 = 0

Câu 4. Tính diện tích hình bình hành ABCD biết A ( 1; -2) ; B ( 2; 0) và D ( -1; 3)

Câu 5. Hai cạnh của hình chữ nhật nằm trên hai đường thẳng 4x – 3y + 5 = 0 và 3x + 4y + 5 = 0 đỉnh A (2; 1) . Tính diện tích của hình chữ nhật

Câu 6. Cho hai điểm A( 2; -1) và B( 0; 100) ; C( 2; -4) .Tính diện tích tam giác ABC ?

Câu 7. Hai cạnh của hình chữ nhật nằm trên hai đường thẳng (a) : 4x – 3y + 5 = 0 và (b) : 3x + 4y – 5 = 0. Biết hình chữ nhật có đỉnh A( 2 ;1). Tính diện tích của hình chữ nhật.

Câu 8. Đường tròn ( C) có tâm I ( -2; -2) và tiếp xúc với đường thẳng d: 5x + 12y – 10 = 0. Tính bán kính R của đường tròn ( C).

3. Đáp án bài tập Cách tính khoảng cách từ một điểm đến một đường thẳng:

Câu	1	2	3	4	5	6	7	8	9	10
Đáp án	D	A	A	D	A	C	A	B	B	D

Câu 1.

Ta có: d ( M ; d ‘ ) = | 2.2 + 2.3 + 5 | / √ 22 + 22 = 15√ 2 / 4

Câu 2.

Ta có: d ( Q ; d ) = | − 2 + 3.1 + 1 | / √ ( − 1 )2 + 32 = √ 10 / 5

Câu 3.

+ Giao điểm A của hai đường thẳng d và ∆ là nghiệm hệ phương trình: { x + y – 2 = 0; 2x + 3y – 5 = 0} => {x = 1; y = 1} => A ( 1; 1)

+ Khoảng cách từ điểm A đến đường thẳng (d’) là : d( A; d’) = 2

Câu 4.

+ Đường thẳng AB: qua A (1; -2); vecto chỉ phương AB (1; 2) nên vecto pháp tuyến n (2; -1)

=> Phương trình AB: 2(x – 1) – 1(y + 2) = 0 hay 2x – y – 4 = 0

+ độ dài đoạn AB: AB = √5

Khoảng cách từ D đến AB: d( D; AB) = 9 / √5

=> Diện tích hình chữ nhật ABCD là S = AB.d( D; AB) = √5. 9 / √5 = 9

Câu 5.

+ Khoảng cách từ đỉnh A(2; 1) đến đường thẳng 4x – 3y + 5 = 0 là 2

+ Khoảng cách từ đỉnh A(2; 1) đến đường thẳng 3x + 4y + 5 = 0 là 3

=> Diện tích hình chữ nhật bằng 2.3 = 6

Câu 6.

+ Phương trình đường thẳng AC: qua A (2; -1); vecto chỉ phương AC (0; -3) nên vecto pháp tuyến n (1; 0)

=> Phương trình AC: 1( x – 2) + 0.(y + 1) = 0 hay x – 2= 0.

+ Độ dài AC = 3 và khoảng cách từ B đến AC là: d(B; AC) = 2

=> Diện tích tam giác ABC là : S = 1/2. AC. d( B;AC) = 1/2 .3.2 = 3 .

Câu 7.

Ta thấy: điểm A không thuộc hai đường thẳng trên.

Độ dài hai cạnh kề của hình chữ nhật bằng khoảng cách từ A đến hai đường thẳng trên.

Độ dài 2 cạnh là: d( A; a) = 2; d(A; b) = 1

Câu 8.

Do đường thẳng d tiếp xúc với đường tròn ( C) nên khoảng cách từ tâm đường tròn ( C) đến đường thẳng d chính là bán kính đường tròn. => R = d(I; d) = 44/13