Tính góc giữa hai mặt phẳng trong không gian là một trong những kiến thức cơ bản của Toán hình lớp 11. Bài viết dưới đây với chủ đề Cách tính góc giữa hai mặt phẳng trong không gian với phương pháp giải chi tiết sẽ giúp các em học sinh ôn tập và biết cách làm bài tập, nhờ đó đạt được kết quả cao trong học tập.
Mục lục bài viết
1. Cách tính góc giữa hai mặt phẳng trong không gian chuẩn:
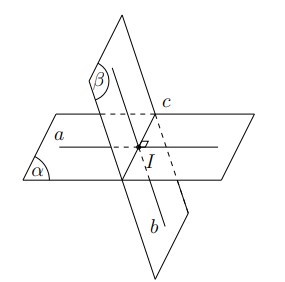
Để tính góc giữa hai mặt phẳng trong không gian, bạn có thể sử dụng một trong các phương pháp sau:
* Phương pháp 1: Sử dụng đường thẳng vuông góc
+ Tìm hai đường thẳng, mỗi đường thẳng nằm trên một mặt phẳng và cả hai đều vuông góc với giao tuyến của hai mặt phẳng đó.
+ Góc giữa hai mặt phẳng chính là góc giữa hai đường thẳng này.
* Phương pháp 2: Sử dụng công thức hình chiếu
+ Xác định diện tích S của hình chiếu của một hình lên mặt phẳng thứ nhất và diện tích S’ của hình chiếu đó lên mặt phẳng thứ hai.
+ Áp dụng công thức S’ = S.cosφ để tìm góc giữa hai mặt phẳng.
* Phương pháp 3: Sử dụng hệ thức lượng trong tam giác
+ Tìm giao tuyến của hai mặt phẳng.
+ Chọn một mặt phẳng thứ ba vuông góc với giao tuyến này và xác định giao tuyến của nó với hai mặt phẳng ban đầu.
+ Góc giữa hai mặt phẳng là góc giữa hai giao tuyến này.
* Phương pháp 4: Sử dụng vectơ pháp tuyến
+ Xác định vectơ pháp tuyến của mỗi mặt phẳng.
+ Tính góc giữa hai mặt phẳng thông qua cosin của góc giữa hai vectơ pháp tuyến này.
2. Góc giữa hai mặt phẳng:
2.1. Định nghĩa:
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Hai mặt phẳng song song hoặc trùng nhau thì góc giữa chúng bằng 0◦.
2.2. Diện tích hình chiếu của một đa giác:
Cho đa giác H nằm trong mặt phẳng (α) có diện tích là S và H0 là hình chiếu vuông góc của H trên mặt phẳng (β). Khi đó diện tích S0 của hình được tính theo công thức như sau:
S0 = S · cos ϕ
với ϕ là góc giữa (α) và (β)
2.3. Tính chất góc giữa hai mặt phẳng:
– Trong trường hợp đặc biệt, nếu hai mặt phẳng song song hoặc trùng nhau, góc giữa chúng bằng 0°, nhưng không được xem là một loại góc riêng biệt.
– Góc giữa hai mặt phẳng không bao giờ lớn hơn 90°, và nếu hai mặt phẳng vuông góc với nhau, góc giữa chúng là 90°.
– Trong không gian ba chiều, góc giữa hai mặt phẳng còn được gọi là “góc khối” vì nó là phần không gian bị giới hạn bởi hai mặt phẳng.
– Việc xác định và tính toán góc giữa hai mặt phẳng là một phần quan trọng trong hình học không gian và có nhiều ứng dụng trong thực tế, như trong kiến trúc, kỹ thuật và thiết kế.
2.4. Các loại góc cơ bản giữa hai mặt phẳng:
Có ba loại góc cơ bản giữa hai mặt phẳng trong không gian ba chiều:
– Góc nhọn: Là góc có số đo nhỏ hơn 90°.
– Góc vuông: Là góc có số đo bằng 90°, tức là hai mặt phẳng vuông góc với nhau.
– Góc tù: Là góc có số đo lớn hơn 90° nhưng không thể xảy ra giữa hai mặt phẳng vì theo định nghĩa, góc giữa hai mặt phẳng không thể lớn hơn 90°.
3. Bài tập vận dụng liên quan kèm lời giải:
Câu 1: Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?
A. Góc giữa hai mặt phẳng (ABC) và (ABD) là ∠CBD
B. Góc giữa hai mặt phẳng (ACD) và (BCD) là ∠AIB
C. (BCD) ⊥ (AIB)
D. (ACD) ⊥ (AIB)
Đáp án: A. Góc giữa hai mặt phẳng (ABC) và (ABD) là ∠CBD
Lời giải chi tiết:
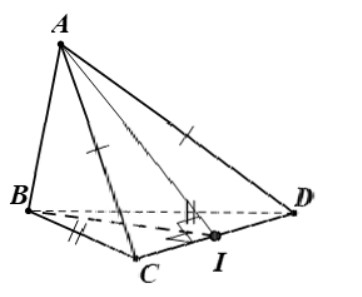
+ Tam giác BCD cân tại B có I trung điểm đáy CD
⇒ CD ⊥ BI (1)
+ Tam giác CAD cân tại A có I trung điểm đáy CD
⇒ CD ⊥ AI (2)
Từ (1) và (2) ⇒ CD ⊥ (ABI).
⇒ (BCD) ⊥ (ABI) Và (ACD) ⊥ (ABI);
Góc giữa hai mặt phẳng (ACD) và (BCD) là ∠AIB .
Vậy A: sai
Câu 2: Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc ∠BAD = 60°. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và SO = 3a/4. Gọi E là trung điểm BC và F là trung điểm BE. Góc giữa hai mặt phẳng (SOF) và (SBC) là
A. 90°
B. 60°
C. 30°
D. 45°
Đáp án: A. 90°
Lời giải chi tiết:
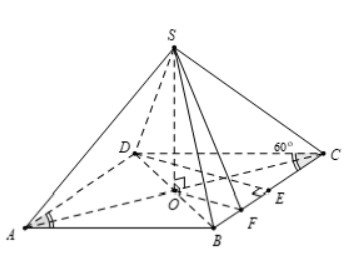
Tam giác BCD có BC = BD và ∠BCD = 60° nên tam giác BCD đều
Lại có E là trung điểm BC ⇒ DE ⊥ BC
Mặt khác, tam giác BDE có OF là đường trung bình
⇒ OF // DE ⇒ BC ⊥ OF (1).
+ Do SO ⊥ (ABCD) ⇒ BC ⊥ SO (2).
+ Từ (1) và (2), suy ra BC ⊥ (SOF) ⇒ (SBC) ⊥ (sOF)
Vậy, góc giữa ( SOF) và( SBC) bằng 90°.
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng
A. 30°
B. 90°
C. 60°
D. 45°
Đáp án: B. 90°
Lời giải chi tiết:
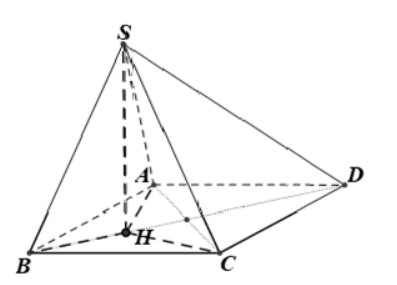
Gọi H là chân đường vuông góc của S xuống mặt phẳng đáy (ABCD) (SH ⊥ (ABCD))
+ Do SA = SB = SC = a nên hình chiếu vuông góc H của S lên mặt phẳng (ABCD) là tâm đường tròn ngoại tiếp tam giác ABC.
+ Mà tam giác ABC cân tại B ( Vì BA = BC = a) ⇒ tâm H phải nằm trên BD ⇒ SH ⊂ (SBD)
Vậy có:
SH ⊥ (ABCD)
SH ⊂ (SBD)
→ (SBD) ⊥ (ABCD)
Nên góc [(SBD) ⊥ (ABCD)] = 90⁰
Câu 4: Cho hình lập phương ABCD.A’B’C’D’. Xét mặt phẳng (A’BD). Trong các mệnh đề sau mệnh đề nào đúng?
A. Góc giữa mặt phẳng ( A’BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng α mà tanα = 1/√2 .
B. Góc giữa mặt phẳng (A’BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng α mà tanα = 1/√3
C. Góc giữa mặt phẳng (A’BD) và các mặt phẳng chứa các cạnh của hình lập phương phụ thuộc vào kích thước của hình lập phương.
D. Góc giữa mặt phẳng ( A’BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng nhau.
Đáp án: D. Góc giữa mặt phẳng ( A’BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng nhau.
Lời giải chi tiết:
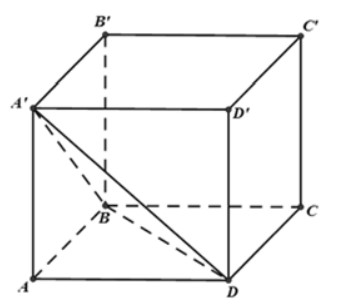
ABCD.A’B’C’D’ là hình lặp phương nên hình chiếu của tam giác A’BD lên các mặt chứa các cạnh của hình lặp phương là các tam giác bằng nhau.
Gọi S1 là diện tích các tam giác này
Lại có S1 = SAD’B.cosα
⇒ Góc giữa mặt phẳng (A’BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng nhau.
Vậy chọn đáp án D.
Câu 5: Cho hình chóp S.ABCD có đáyABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy và SA = a. Góc giữa hai mặt phẳng (SBC) và (SCD) bằng bao nhiêu?
A. 30°
B. 45°
C. 90°
D. 60°
Đáp án: D. 60°
Lời giải chi tiết:
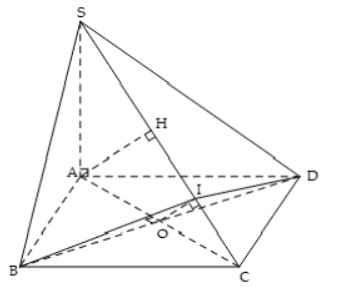
Ta có: SC ⊥ BD (vì BD ⊥ AC, BD ⊥ SA)
Trong mặt phẳng (SAC) , kẻ OI ⊥ SC thì ta có SC ⊥ (BID)
Khi đó ((SCB), (SCD)) = ∠BID
Trong tam giác SAC, kẻ đường cao AH thì AH = a(√2/√3)
Mà O là trung điểm AC và OI // AH nên OI = a/√6
Tam giác IOD vuông tại O có ∠OID = √3 ⇒ ∠OID = 60°
Vậy hai mặt phẳng (SBC) và (SCD) hợp với nhau một góc 60°
Chọn D.
Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA ⊥ (ABCD); SA = x. Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60°.
A. x = 3a/2
B. x = a/2
C. x = a
D. x = 2a
Đáp án: D. 60°
Lời giải chi tiết:
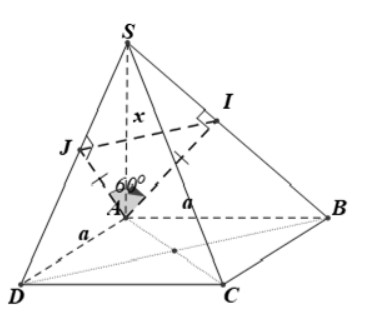
* Trong (SAB) dựng AI ⊥ SB ta chứng minh được AI ⊥ (SBC) (1)
Trong (SAD) dựng AJ ⊥ SD ta chứng minh được AJ ⊥ (SCD) (2)
Từ (1) và (2) ⇒ góc ((SBC), (SCD)) = (AI, AJ) = ∠IAJ
* Ta chứng minh được AI = AJ. Do đó, nếu góc ∠IAJ = 60° thì ΔAIJ đều ⇒ AI = AJ = IJ
Tam giác SAB vuông tại A có AI là đường cao
→ AI . SB = SA . AB = AI = (SA . AB)/SB (3)
Và có SA² = SI. SB → SI = SA²/SB (4)
Ta chứng minh được
IJ // BD → IJ/BD = SI/SB
→ IJ = (SI . BD)/SB = (SA² . BD)/SB² (5)
Thế (3) và (5) vào AI = IJ → AB = (SA . BD)/SB
⇔AB . SB = SA . BD ⇔ ![]()
⇔x² + a² = 2x² ⇔x = a
THAM KHẢO THÊM:




