Phương trình lượng giác là phương trình chứa các tỉ số lượng giác. Việc tìm nghiệm của phương trình lượng giác đòi hỏi phải tìm giá trị của các góc thỏa mãn phương trình. Sau đây là Cách giải phương trình lượng giác cơ bản và nâng cao.
Mục lục bài viết
1. Cách giải phương trình lượng giác cơ bản và nâng cao:
Phương trình lượng giác là một phương trình chứa các hàm lượng giác của một biến số. Phương trình lượng giác có thể được giải bằng nhiều cách, tùy thuộc vào dạng và độ phức tạp của nó. Một số phương pháp thường được sử dụng là:
– Đặt biến: Đây là cách đơn giản nhất, chỉ cần đặt một biến mới bằng một hàm lượng giác của biến cũ, sau đó giải phương trình đa thức với biến mới, rồi thay ngược lại để tìm nghiệm của biến cũ.
– Công thức lượng giác: Đây là cách sử dụng các công thức lượng giác như công thức cộng, trừ, nhân, chia, lập luận, nửa góc, ba góc… để biến đổi phương trình lượng giác thành một dạng đơn giản hơn, rồi tìm nghiệm bằng cách so sánh với các giá trị đã biết của các hàm lượng giác.
– Đồ thị: Vẽ đồ thị của các hàm lượng giác trong phương trình, rồi xác định các điểm cắt nhau của các đồ thị đó. Nghiệm của phương trình chính là hoành độ của các điểm cắt nhau. Cách này thường được dùng khi không thể giải phương trình bằng phương pháp đại số.
Chi tiết hơn thì như sau:
– Bước 1. Xác định hàm số và khoảng: Bắt đầu bằng cách xác định hàm lượng giác nào bạn đang xử lý (sin, cos, tang, cotang) và khoảng mà bạn cần tìm nghiệm.
– Bước 2. Cô lập hàm lượng giác: Nếu phương trình phức tạp hơn, hãy nhắm đến việc cô lập hàm lượng giác ở một vế của phương trình.
– Bước 3. Giải phương trình: Giải phương trình như cách giải phương trình đại số cơ bản.
– Bước 4. Xác định chu kỳ của hàm số: Mỗi hàm lượng giác có một khoảng sau đó nó lặp lại các giá trị của nó. Biết được khoảng này là công cụ để tìm ra tất cả các nghiệm khả thi trong khoảng nhất định.
– Bước 5. Tìm tất cả các nghiệm trong khoảng: Sử dụng khoảng, tính toán tất cả các nghiệm có thể có trong khoảng nhất định. Hãy nhớ rằng, các hàm lượng giác có thể có nhiều nghiệm hợp lệ trong bất kỳ khoảng nào.
* Ví dụ: Giải sin(x) = 0,5 cho x trong khoảng [0, 360°).
Lời giải:
Cần xử lý hàm sin và khoảng là [0, 360°).
Hàm sin đã bị cô lập.
Lời giải chính được tìm ra bằng cách xét góc đặc biệt có sin bằng 0,5. Chúng ta biết sin(30°) = 0,5, vì vậy x = 30° là nghiệm chính.
Hàm sin có chu kỳ 360°. Điều này có nghĩa là sau mỗi 360°, các giá trị sin sẽ lặp lại.
Để tìm mọi nghiệm, ta xét tính đối xứng của hàm sin. Biết rằng sin(x) = sin(180° – x). Vì vậy, nghiệm khác trong khoảng đó là 180° – 30° = 150°.
Do đó, nghiệm của phương trình trong khoảng đã cho là 30° và 150°.
2. Các hàm lượng giác:
Để hiểu sâu hơn về cách giải các phương trình lượng giác cơ bản, điều cần thiết là phải đi sâu hơn vào các tính chất và đặc điểm của hàm lượng giác.
– Hàm sin
Hàm sin, ký hiệu là sin(x), là hàm tuần hoàn có chu kỳ 360° hoặc 2π radian. Hàm sin bắt đầu từ 0, đạt tối đa 1 ở 90°, quay về 0 ở 180°, đạt tối thiểu -1 ở 270° và trở về 0 ở 360°.
Đặc điểm chính:
+ Biên độ: Giá trị tối đa của hàm sin là 1 và giá trị tối thiểu là -1.
+ Chu kỳ: Hàm sin lặp lại các giá trị của nó sau mỗi 360° hoặc 2π radian.
+ Tính đối xứng: Hàm sin đối xứng qua trục y.
– Hàm cosin
Hàm cosin, ký hiệu là cos(x), cũng là một hàm tuần hoàn có chu kỳ 360° hoặc 2π radian. Hàm cosin bắt đầu từ 1, tiến tới 0 ở 90°, đạt tối thiểu -1 ở 180°, trở về 0 ở 270° và quay trở lại 1 ở 360.
Đặc điểm chính:
+ Biên độ: Giá trị tối đa của hàm cosine là 1 và giá trị tối thiểu là -1.
+ Chu kỳ: Hàm cosin lặp lại các giá trị của nó sau mỗi 360° hoặc 2π radian.
+ Tính đối xứng: Hàm cosine đối xứng qua gốc tọa độ.
– Hàm tiếp tuyến
Hàm tiếp tuyến, ký hiệu là tan(x), khác với sin và cos. Đó là tỷ số giữa sin và cos. Hàm có các tiệm cận đứng (các giá trị trong đó hàm không xác định) ở bội số lẻ của 90°.
Đặc điểm chính:
+ Biên độ: Hàm tiếp tuyến không có biên độ cố định. Nó có thể nhận bất kỳ giá trị thực nào.
+ Chu kỳ: Hàm tiếp tuyến lặp lại các giá trị của nó sau mỗi 180° hoặc π radian.
+ Tính đối xứng: Hàm tiếp tuyến đối xứng qua gốc tọa độ.
* Những điểm chính cần nhớ
– Tính đối xứng trong các hàm lượng giác: Hàm sin và cos có tính đối xứng, thường dẫn đến nhiều nghiệm trong một chu kỳ. Tuy nhiên, tiếp tuyến lặp lại sau 180° và cần xem xét các giải pháp bổ sung dựa trên tính đối xứng của nó.
– Giải pháp chính và giải pháp bổ sung: Giải pháp đầu tiên bạn tìm thấy (chính) không phải là giải pháp duy nhất. Sử dụng khoảng của hàm số để khám phá các giải pháp bổ sung trong khoảng đó.
– Kiểm tra lời giải: Luôn xác minh lời giải của bạn bằng cách thay chúng trở lại phương trình ban đầu để đảm bảo chúng thỏa mãn phương trình.
3. Các công thức lượng giác:
Có một số công thức quan trọng chúng ta phải ghi nhớ để giải các bài toán và tình huống lượng giác khác nhau. Một số được đưa ra dưới đây:
cos(2nπ + x) = cos x
sin(2nπ + x) = sin x
cos (-x) = cos x
sin(-x) = – sin x
cos(x + y) = cos x cos y – sin x sin y
cox(x – y) = cos x cos y + sin x sin y
sin(x + y) = sin x cos y + cos x sin y
sin(x – y) = sin x cos y – cos x sin y
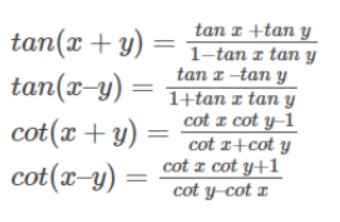
cos 2x = cos2x – sin2x = 2 cos2x – 1 = 1 – 2 sin2 x
sin 2x = 2 sin x cos x
sin 3x = 3 sin x – 4 sin3x
cos 3x = 4 cos3x – 3 cos x
cos x + cos y = 2 cos{(x+y)/2} cos{(x-y)/2}
cos x – cos y = -2 sin{(x+y)/2} sin{(x-y)/2}
sin x + sin y = 2 sin{(x+y)/2} cos{(x-y)/2}
sin x – sin y = 2 cos{(x+y)/2} sin{(x-y)/2}
2 cos x cos y = cos (x + y) + cos (x – y)
-2 sin x sin y = cos (x + y) – cos (x – y)
2 sin x cos y = sin (x + y) + sin (x – y)
2 cos x sin y = sin (x + y) – sin (x – y)
cos(π – x) = -cos x
cos(π + x) = -cos x
sin(π – x) = sin x
sin(π + x) = -sin x
cos(2π – x) = cos x
sin(2π – x) = – sin x
cos (π/2 + x) = – sin x
sin (π/2 + x) = cos x
4. Bài tập vận dụng và lời giải:
Bài 1: Giải phương trình: 2sinx + 1 = 0
Lời giải:
Chuyển 1 sang vế phải:
2sinx = -1
Chia hai vế cho 2:
sinx = -1/2
Tìm các giá trị của x thỏa mãn phương trình bằng cách sử dụng bảng giá trị hoặc công thức đặc biệt:
sinx = -1/2 khi x = 7π/6 + k2π hoặc x = 11π/6 + k2π (k là số nguyên)
Vậy nghiệm của phương trình là x = 7π/6 + k2π hoặc x = 11π/6 + k2π (k là số nguyên)
Bài 2: Nếu sinθ + cos θ = 1 thì giá trị tổng quát của θ là bao nhiêu?
Lời giải:
sin θ + cos θ = 1 ⇒ (1 / √2) sin θ + (1 / √2) cos θ = 1 / √2
Chia cho √[12 + 12] = √2,
Ta có, sin (θ + π / 4) = [1/ √2] = sin π / 4
⇒ θ + π / 4 = nπ + (−1)n [π / 4]
⇒ θ = nπ + (−1)n [π / 4] − π / 4
Bài 3: Nếu hai góc ở đáy của một tam giác là (22.5)o và (112.5)o thì tỉ lệ giữa chiều cao của tam giác và chiều dài đáy là bao nhiêu?
Lời giải:
Trong ∆ ACD, h/sin (67.5o) = AC/sin 90o
⇒ h / AC = sin (67.5o) ….(i)
Trong ΔABC, AC/sin(22.5o) = x/sin45o
⇒ AC/x = √2/sin(22.5o) …..(ii)
Từ (i) và (ii),
h/x = 1/2
Bài 4: Nếu các góc của một tam giác có tỉ lệ 1 : 2 : 7 thì tỉ số giữa cạnh lớn nhất và cạnh nhỏ nhất là bao nhiêu?
Lời giải:
x + 2x + 7x = 180o ⇒ x = 18o
Vậy các góc là 18o, 36o, 126o
Cạnh lớn nhất = sin ( 126o)
Cạnh nhỏ nhất = sin (18o) và
Tỷ số = sin 126o / sin (18o) = [√5 + 1] / [√ 5 − 1]
Bài 5: Nếu các góc A, B, C của một tam giác thuộc A.P., và các cạnh a, b, c đối diện với các góc này thuộc G.P. thì a2, b2, c2 sắp xếp theo thứ tự nào?
Lời giải:
Vì A, B và C thuộc A.P. nên B = 60∘ và b2 = ac
cos B = a2 + c2 − b2 / 2ac
⇒ 1/2 = a2 + c2 − b2 / 2b2 (∵ b2 = ac)
b2= a2 + c2 − b2
⇒ a2 + c2 = 2b2




