Dạng toán hiệu tỉ lớp 5 cơ bản và nâng cao là dạng toán phổ biến . Dưới đây, chúng tôi sẽ hướng dẫn các em phương pháp giải bài, mời quý phụ huynh và các em đọc và chú ý cách làm như sau nhé.
Mục lục bài viết
1. Bài toán về hiệu tỉ tổng tỉ là gì?
Bài toán về hiệu tỉ là một loại bài toán toán học đòi hỏi tính toán các phép cộng, trừ, và chia. Đây là bài toán liên quan đến việc xác định tổng, hiệu, và tỉ số của các số được cho.
Tổng là kết quả của phép cộng giữa hai hoặc nhiều số. Ví dụ, khi bạn cộng 3 và 4, kết quả là 7.
Hiệu là kết quả của phép trừ giữa hai số. Ví dụ, khi bạn trừ 3 từ 8, kết quả là 5.
Tỉ số thể hiện một phần của một số so với số khác. Nó thể hiện số này lớn bằng bao nhiêu lần hoặc bằng bao nhiêu phần của số kia. Ví dụ, tỉ số của 3 so với 5 là 3/5.
Bài toán tổng tỉ đưa ra thông tin về tổng và tỉ số của hai số và yêu cầu bạn tìm hai số đó. Ví dụ, nếu tổng của hai số là 10 và tỉ số của chúng là 2/5, bài toán yêu cầu bạn tìm hai số đó là bao nhiêu.
Bài toán hiệu tỉ cung cấp thông tin về hiệu và tỉ số của hai số và yêu cầu bạn tìm hai số đó. Ví dụ, nếu hiệu của hai số là 7 và tỉ số của chúng là 3/4, bài toán đặt câu hỏi về giá trị của hai số đó.
Những bài toán này đòi hỏi kỹ năng tính toán, đồng thời yêu cầu hiểu biết sâu sắc về các phép toán cơ bản như cộng, trừ, và chia để giải quyết vấn đề. Chúng cũng giúp rèn luyện khả năng phân tích và suy luận trong việc áp dụng kiến thức toán học vào thực tế.
2. Cách giải các dạng toán hiệu tỉ lớp 5 cơ bản và nâng cao:
2.1. Cách giải chung bài toán dạng hiệu tỉ:
Để giải bài toán hiệu tỉ, chúng ta có thể thực hiện các bước sau:
– Bước 1: Dựa vào tỉ số, ta lập sơ đồ các phần bằng nhau để hiểu rõ tỉ lệ giữa các số.
– Bước 2: Xác định số lượng phần và từ đó suy ra giá trị một phần bằng bao nhiêu đơn vị, thông qua hiệu của tỉ.
– Bước 3: Xác định số lớn và số bé theo cách sau:
+ Số lớn = số lượng phần của số lớn × giá trị của một phần
+ Số bé = số lượng phần của số bé × giá trị của một phần
Ví dụ, giả sử có một bài toán với tỉ số là 2/5 và hiệu là 7. Bước đầu tiên, chúng ta sẽ chia một đoạn thành 5 phần bằng nhau. Từ đó, khi hiệu của số lớn và số bé là 7, chúng ta có thể suy ra giá trị của mỗi phần là 7/3. Sau đó, với số phần của số lớn và số bé được xác định từ tỉ số, chúng ta có thể tính được giá trị cuối cùng của số lớn và số bé thông qua các công thức đã nêu ở bước 3.
Bài toán này yêu cầu sự linh hoạt trong việc hiểu và áp dụng tỉ lệ, cũng như kỹ năng tính toán để tìm ra giá trị chính xác của các số trong bài toán.
Một số trường hợp đặc biệt khác
Nhiều trường hợp khi đề bài không cho các dữ kiện đầy đủ về hiệu và tỉ số, mà có thể cho dữ kiện như sau:
– TH1: Thiếu hiệu (cho biết tỉ số, không có biết hiệu số)
– TH2: Thiếu tỉ (cho biết hiệu số, không cho biết tỉ số)
– TH3: Cho dữ kiện thêm, bớt số, tạo hiệu (tỉ) mới tìm số ban đầu
Phương pháp: Với những bài toán cho dữ kiện như vậy, cần tiến hành thêm một bước chuyển về bài toán cơ bản.
2.2. Các bài toán hiệu tỉ lớp 5 nâng cao:
Trong một số bài toán, hiệu số hoặc tỉ số không được cho trước. Chúng ta cần phải đi tìm hiệu số hoặc tỉ số trước rồi tiếp tục làm theo các bước như trên
Dạng bài tỉ số bị ẩn
Dạng bài này chúng ta sử dụng tính chất sau đây: Nếu gấp số thứ nhất lên a lần sẽ bằng gấp số thứ hai lên b lần thì ta coi số thứ nhất là b phần, số thứ hai sẽ là a phần hay nói cách khác, tỉ số của hai số là ab
Ví dụ:
Có hai thùng đựng dầu, thùng thứ nhất đựng nhiều hơn thùng thứ hai 24 lít dầu. Biết rằng 5 lần số dầu thùng thứ nhất thì bằng 3 lần số dầu thùng thứ hai. Tìm số dầu trong mỗi thùng ?
Cách giải
Vì 5 lần số dầu thùng thứ nhất bằng 3 lần số dầu thùng thứ hai nên ta coi số dầu thùng thứ nhất là 3 phần thì số dầu thùng thứ hai sẽ là:
5×3:3=5 (phần )
Vậy ta có sơ đồ sau:
Hiệu số phần bằng nhau là:
5−3=2 (phần )
Giá trị mỗi phần là:
24:2=12 (lít )
Vậy số dầu thùng thứ nhất là:
12×3=36 (lít )
Số dầu thùng thứ hai là:
12×5=60 (lít )
Đáp số : Thùng thứ nhất có 36 lít dầu, thùng thứ hai có 60 lít dầu.
Dạng bài hiệu số bị ẩn
Dạng bài này chúng ta sử dụng hai tính chất sau đây :
– Nếu thêm (hoặc bớt) ở số bị trừ bao nhiêu đơn vị thì hiệu sẽ tăng (hoặc giảm) bấy nhiêu đơn vị.
– Nếu thêm (hoặc bớt) ở số trừ bao nhiêu đơn vị thì hiệu sẽ giảm (hoặc tăng) bấy nhiêu đơn vị.
Ví dụ:
Tìm hai số biết rằng số thứ nhất bằng 34 số thứ hai và nếu thêm vào số bé 3 đơn vị và bớt đi ở số lớn 2 đơn vị thì số lớn còn hơn số bé 1 đơn vị?.
Cách giải:
Ta coi số lớn là số bị trừ và số bé là số trừ. Do đó:
Nếu thêm vào số bé 3 đơn vị thì hiệu hai số sẽ giảm đi 3 đơn vị
Nếu bớt ở số lớn 2 đơn vị thì hiệu hai số sẽ giảm đi 2 đơn vị
Vậy tất cả hiệu hai số sẽ giảm đi:
3+2=5 ( đơn vị )
Vì bớt đi 5 đơn vị mà hiệu hai số còn 1 đơn vị nên ban đầu hiệu hai số là :
1+5=6 (đơn vị )
Vậy ta có sơ đồ sau:
Hiệu số phần bằng nhau là :
4−3=1 ( phần )
Giá trị của một phần là :
6:1=6 (đơn vị )
Vậy số bé là :
6×3=18
Số lớn là :
6×4=24
Đáp số : Số bé là 18 , số lớn là 24
3. Bài tập vận dụng:
Bài 1: Hiệu hai số bằng 4104. Biết rằng nếu xóa chữ số 0 ở hàng đơn vị của số bị trừ thì được số trừ. Tìm hai số đó.
Xóa chữ số 0 ở số bị trừ được số trừ, cho ta biết số bị trừ gấp 10 lần số trừ.
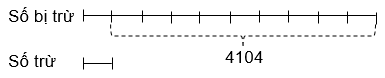
Hiệu số phần bằng nhau là:
10 – 1 = 9 (phần)
Số trừ là:
4104 : 9 = 456
Số bị trừ là:
456 + 4104 = 4560
Đáp số: 4560 và 456
Bài 2: Có hai kho thóc, kho A chứa nhiều hơn kho B 60 tấn. Biết sau khi chuyển từ kho A sang kho B 50 tấn thì số thóc còn lại trong kho A bằng 4/5 số thóc trong kho B. Vậy lúc đầu mỗi kho chưa bao nhiêu tấn thóc?
Sau khi chuyển 50 tấn thóc từ kho A sang kho B thì kho B sẽ nhiều hơn kho A là:
50 x 2 – 60 = 40 (tấn)
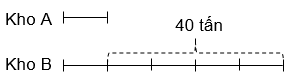
Hiệu số phần bằng nhau:
5 – 4 = 1 (phần)
1 phần ứng với 40 tấn vậy số thóc kho A hiện nay là:
40 x 4 = 160 (tấn)
Số thóc kho A ban đầu là:
160 + 50 = 210 (tấn)
Số thóc kho B là:
210 – 60 = 150 (tấn)
Đáp số: Kho A: 210 tấn
Kho B: 150 tấn.
Bài 3: Có 3 nhóm học sinh đi lao động. Nếu lấy 25 số học sinh của nhóm thứ nhất chia đều cho 2 nhóm kia thì số học sinh của 3 nhóm sẽ bằng nhau. Nếu bớt ở nhóm thứ nhất 3 em thì số học sinh còn lại của nhóm này sẽ bằng tổng số học sinh của 2 nhóm kia. Tính số học sinh đi lao động?
Phân số chỉ số học sinh còn lại của nhóm 1 sau khi chia đều cho 2 nhóm kia là:
1 – 25 = 35 (nhóm 1)
Mỗi nhóm 2 và 3 nhận được là:
25 : 2 = 15 (nhóm 1)
Phân số chỉ số học sinh của nhóm 2 và 3 là:
35 – 15 = 25 (nhóm 1)
Phân số chỉ tổng số học sinh của nhóm 2 và nhóm 3 là:
25 x 2 = 45 (nhóm 1)
Phân số chỉ 3 học sinh bớt ở nhóm 1 là:
1 – 45 = 15 (nhóm 1)
Số học sinh nhóm 1 là:
3 x 5 = 15 (em)
Tổng số học sinh 2 nhóm 2 và 3 là:
15 x 45 = 12 (em)
Số học sinh đi lao động:
15 + 12 = 27 (học sinh)
Đáp số: 27 học sinh




