Bài viết Cách chứng minh tiếp tuyến của một đường tròn lớp 9 với phương pháp giải chi tiết và các bài tập vận dụng liên quan sẽ giúp các em học sinh ôn tập và biết cách làm bài tập Cách chứng minh tiếp tuyến của một đường tròn. Xin mời các em cùng theo dõi bài viết dưới đây.
Mục lục bài viết
1. Cách chứng minh tiếp tuyến của một đường tròn:
Để chứng minh đường thẳng d là tia tiếp tuyến của đường tròn (O;R) tại điểm A ta dùng các cách sau đây:
– Cách 1: Kẻ OA ⊥ d tại A, chứng minh OA = R.
– Cách 2: Đường thẳng d đi qua A ∈ (O ; R) thì ta cần chứng minh OA ⊥ d tại điểm A.
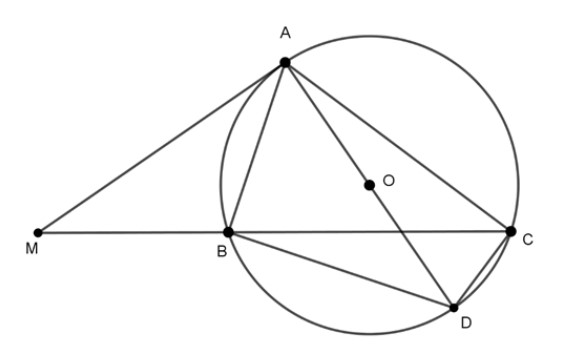
Ví dụ : Cho ΔABC nội tiếp đường tròn (O), (AB < AC). Trên tia đối của tia BC lấy điểm M sao cho MA2 = MB.MC. Chứng minh rằng: MA là tiếp tuyến của đường tròn (O).


2. Đường tiếp tuyến của một đường tròn:
Đường tiếp tuyến của một đường tròn được định nghĩa là một đường thẳng chạm hoặc cắt đường tròn chỉ tại một điểm. Tiếp tuyến là một đường thẳng không bao giờ đi vào bên trong đường tròn.
Hình dưới đây cho thấy một đường tròn với một điểm P. Một tiếp tuyến L đi qua P. Đây là một ví dụ về tiếp tuyến của một đường tròn.
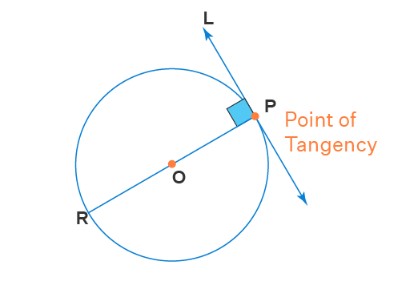
Điểm tiếp tuyến được định nghĩa là điểm giao nhau duy nhất nơi đường thẳng chạm hoặc cắt đường tròn. Trong hình trên, điểm P đại diện cho điểm tiếp tuyến.
Tiếp tuyến có hai tính chất quan trọng:
– Một tiếp tuyến tiếp giáp với một đường tròn chỉ tại một điểm.
– Tiếp tuyến là một đường thẳng không bao giờ đi vào bên trong đường tròn.
– Tiếp tuyến tiếp giáp với bán kính của đường tròn tại điểm tiếp tuyến ở một góc vuông.
Có hai định lý quan trọng nhất về tiếp tuyến của một đường tròn. Đó là định lý tiếp tuyến với bán kính của đường tròn và định lý hai tiếp tuyến.
* Định lý tiếp tuyến với bán kính đường tròn:
Tiếp tuyến tại bất kỳ điểm nào của đường tròn đều vuông góc với bán kính qua điểm tiếp tuyến.
– Cho trước: Tiếp tuyến PL với một đường tròn S (với tâm đường tròn là O), và điểm tiếp tuyến là A.
– Chứng minh: OA vuông góc với PL tiếp tuyến.
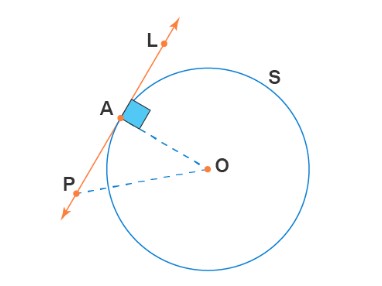
Chứng minh:
Điểm P nằm ngoài đường tròn. Khi nối PO, chúng ta nhận được PO > OA (bán kính của một đường tròn). Điều kiện này áp dụng cho mọi điểm trên đường tiếp tuyến PL ngoại trừ điểm A.
PO > OA cho thấy rằng OA là khoảng cách ngắn nhất trong tất cả các khoảng cách của điểm O đến các điểm khác trên đường tiếp tuyến PL.
Do đó ta chứng minh được: OA vuông góc với PL.
* Định lý hai tiếp tuyến:
Giả sử rằng hai tiếp tuyến được vẽ vào một đường tròn từ một điểm bên ngoài C. Ta được các điểm tiếp tuyến là A và B, như trong hình dưới đây.
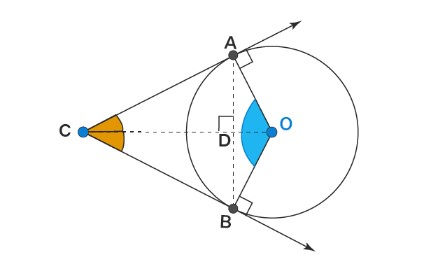
Định lý phát biểu như sau:
– Độ dài của hai tiếp tuyến này bằng nhau, nghĩa là CA = CB.
– Hai tiếp tuyến phụ các góc bằng nhau ở tâm O, nghĩa là ∠COA = ∠COB.
– Góc giữa các tiếp tuyến được chia đôi bởi đường nối từ điểm bên ngoài C và tâm O của đường tròn, nghĩa là ∠ACO = ∠BCO.
Chứng minh:
Cả ba phát biểu được chứng minh nếu chúng ta chỉ ra rằng ΔCAO tương đẳng với ΔCBO.
So sánh hai tam giác, chúng ta thấy rằng:
– OA = OB (bán kính của cùng một đường tròn)
– OC = OC (cạnh chung)
– ∠OAC = ∠OBC = 90° (Tiếp tuyến vẽ thành một đường tròn vuông góc với bán kính tại điểm tiếp tuyến)
Do đó, ΔCAO tương đẳng với ΔCBO, và ba phát biểu trên của định lí hai tiếp tuyến đều đúng.
Tiếp tuyến là một đường thẳng. Để viết phương trình của một đường thẳng chúng ta cần hai yếu tố là, hệ số góc (m) và một điểm trên đường thẳng ấy.
Phương trình tổng quát của tiếp tuyến với một đường tròn là:
1) Tiếp tuyến với phương trình đường tròn x² + y² = a² với một đường thẳng y = mx + c được cho bởi phương trình:
y = mx ± a √[1+ m2].
2) Tiếp tuyến với phương trình đường tròn x²+ y² = a² tại (a1,b1):
là xa1+ yb1 = a²
Do đó, phương trình tiếp tuyến có của một đường tròn là:
xa1+yb1 = a²
trong đó (a1,b1) là tọa độ mà từ đó tiếp tuyến được tạo ra.
3. Bài tập chứng minh tiếp tuyến của một đường tròn:
Bài 1: Cho đường tròn tâm O đường kính AB. C là một điểm thay đổi trên đường tròn (O). Tiếp tuyến tại C của (O) cắt AB tại D. Đường thẳng qua O và vuông góc với phân giác của ∠ODM, cắt CD tại M. Qua M kẻ đường thẳng d song song với AB. Chứng minh d là tiếp tuyến của (O).
Lời giải chi tiết:
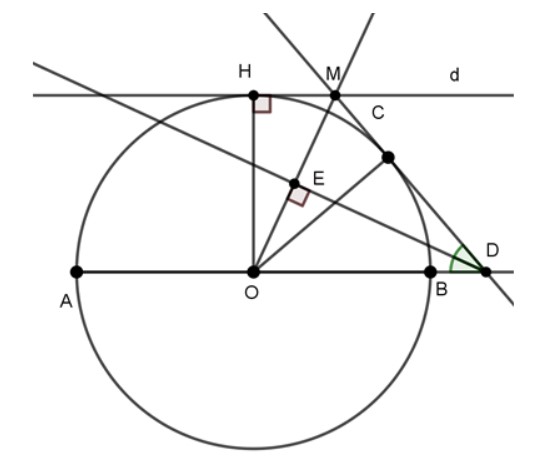
Kẻ OH ⊥ d → ∠OHM = 90⁰.
Ta có CD là tiếp tuyến của (O) nên OC ⊥ CD tại C ⇒ ∠OCM = 90⁰.
Gọi E là giao điểm của tia phân giác ∠ODM với OM.
Xét tam giác MDO có : DE là phân giác ∠ODM, DE là đường cao
⇒ ΔDOM cân tại D
⇒ ∠DMO = ∠DOM (hai góc ở đáy)
Ta lại có : d//AB ⇒∠HMO = ∠DOM (hai góc so le trong).
⇒ ∠HMO = ∠DMO.
Xét ΔOHM và ΔOCM , có :
∠OHM = ∠OCM = 90⁰
OM: cạnh chung
∠HMO = ∠DMO.
⇒ ΔOHM = Δ OCM (cạnh huyền – góc nhọn)
⇒ OH = OC = R (hai cạnh tương ứng)
⇒ H ∈ (O;R)
Do đó d là tiếp tuyến của (O;R).
Bài 2: Cho tam giác ABC nhọn. Vẽ đường tròn tâm O đường kính BC, cắt AB,AC lần lượt tại E và F. BF và CE cắt nhau tại I. Gọi M là trung điểm của AI. Chứng minh MF là tiếp tuyến của (O).
Lời giải chi tiết:
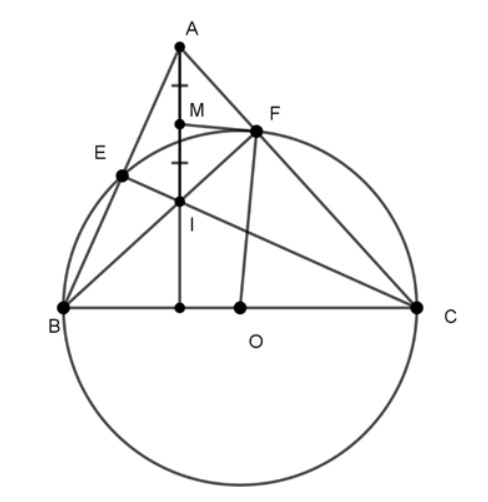
Ta có: ∠BFC = ∠BEC = 90⁰ (góc nội tiếp chắn nửa đường tròn)
⇒ BF ⊥ AC , CE ⊥ AB
Xét tam giác ABC, có BF ∩ CE = {I}
⇒ I là trực tâm tam giác ABC
Gọi H là giao điểm của AI với BC
⇒ AH ⊥ BC tại H
Xét tam giác AFI vuông tại F, có M là trung điểm của AI
⇒ FM = MA = MI
⇒ ΔFMA cân tại M
⇒∠MAF = ∠MFA (hai góc ở đáy) (1)
Xét tam giác OFC, có OF = OC
⇒ FOC cân tại O
⇒∠OFC = ∠ OCF (hai góc ở đáy) (2)
Xét tam giác AHC vuông tại H, có: ∠MAF + ∠OCF =90⁰ (hai góc phụ nhau)(3)
Từ (1), (2) và (3) ∠MAF + ∠OCF =90⁰
Mà ∠MFO + ∠MFA + ∠OFC = 180⁰.
→ ∠MFO = 90⁰
⇒ MF ⊥ OF
Vậy MF là tiếp tuyến của (O).
Bài 3: Cho nửa đường tròn tâm O đường kính AB. Ax, By là hai tiếp tuyến của (O) (Ax, By cùng phía đối với đường thẳng AB). Trên Ax lấy điểm C, trên By lấy điểm D sao cho
AC. BD = ¼AB²
Khi đó:
a. CD tiếp xúc với đường tròn (O)
b. CD cắt đường tròn (O) tại hai điểm phân biệt
c. CD không có điểm chung với (O)
d. CD = R2
Đáp án: A
Lời giải chi tiết:
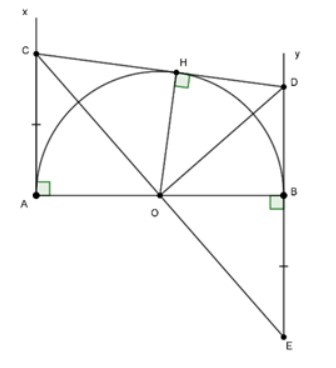
Trên tia đối của tia BD lấy điểm E sao cho BE = AC
Kẻ OH ⊥ CD
Ta có: AC.BD = ¼.AB² = ¼(2R)² = R²
Mà AC = BE ⇒ BE.BD = R2 = OB2
⇒ ΔDOE vuông tại O
Xét ΔOAC và ΔOBE , ta có:
∠OAC = ∠OBE = 90⁰
AC = BE (gt)
OA = OB (=R)
⇒ ΔOAC = ΔOBE (g-g-g)
⇈ ∠ AOC = ∠BOE (hai góc tương ứng)
Ta có: ∠COE = ∠COB + ∠BOE = ∠COB + ∠AOC = ∠AOB = 180⁰
Nên C, O, E thẳng hàng
Xét tam giác DCE, có:
OD vừa là đường cao vừa là đường trung tuyến của △CDE nên OD cũng là đường phân giác.
⇒ ∠HDO = ∠BDO
(DO là phân giác ∠CDE)
Xét ΔOHD và ΔOBD , có:
OD chung
∠OHD = ∠OBD = 90⁰
∠HDO = ∠BDO (Cmt)
⇒ ΔOHD = ΔOBD (cạnh huyền – góc nhọn)
⇒ OH = OB ⇒ CD tiếp xúc với đường tròn (O).
Bài 4: Cho tam giác ABC cân tại A, đường cao AH và BK cắt nhau ở I. Khi đó:
a. AK là tiếp tuyến của đường tròn đường kính AI
b. BK là tiếp tuyến của đường tròn đường kính AI
c. BH là tiếp tuyến của đường tròn đường kính AI
d. HK là tiếp tuyến của đường tròn đường kính AI
Đáp án: D
Lời giải chi tiết:
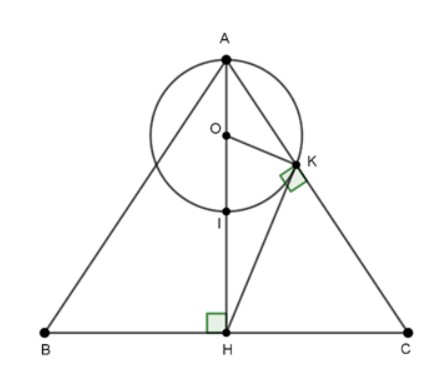
Gọi O là trung điểm của AI, khi đó: KO là đường trung tuyến của tam giác vuông AKO.
⇒ AO = IO = OK.
⇒ ΔOAK cân tại O
⇒∠OAK = ∠OKA(hai góc ở đáy) (1)
Xét tam giác BKC vuông tại K, có H là trung điểm của BC(do tam giác ABC cân tại A)
⇒ BH = HK = HC.
⇒ ΔHCK cân tại H
⇒∠HKC = ∠HCK (hai góc ở đáy) (2)
Ta lại có: ∠OAK + ∠HCK = 90⁰ (hai góc nhọn phụ nhau trong tam giác vuông AHC)(3)
Từ (1), (2) và (3) suy ra:
∠OKA + ∠HCK = 90⁰ hay ∠OKH = 90⁰
Từ đó suy ra rằng HK là tiếp tuyến của đường tròn đường kính AI.
THAM KHẢO THÊM:




