Phương trình tiếp tuyến là một kiến thức trọng tâm trong Toán học 11. Bài viết dưới đây với chủ đề Các dạng bài tập về tiếp tuyến lớp 11 và cách giải sẽ giúp các em học sinh nắm vững lý thuyết, biết cách làm bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán 11.
Mục lục bài viết
1. Dạng bài tập Viết phương trình tiếp tuyến khi biết tiếp điểm:
* Phương pháp giải:
Phương trình tiếp tuyến với đồ thị (C): y = f(x) tại điểm M0(x0; f(x0)) là:
y = f’(x0) . (x – x0) + f(x0)
Trong đó:
M0 (x0; y0) gọi là tiếp điểm.
k = f'(x0) là hệ số góc.
* Để viết phương trình tiếp tuyến của một đồ thị hàm số tại một điểm, bạn cần làm theo các bước sau:
– Xác định hàm số của đồ thị mà bạn đang xét, ví dụ: f(x) .
– Tìm tọa độ của tiếp điểm. Giả sử tiếp điểm có tọa độ là (x0, y0).
– Tính đạo hàm của hàm số tại điểm đó để tìm hệ số góc của tiếp tuyến, tức là f'(x0).
– Sử dụng công thức của phương trình tiếp tuyến: ( y – y0 = f'(x0) . (x – x0).
– Thay các giá trị của x0, y0 và f'(x0) vào công thức để có phương trình cụ thể.
* Chú ý:
– Nếu cho x0 thì thế vào y = f(x) tìm y0.
– Nếu cho y0 thì thế vào y = f(x) tìm x0.
* Ví dụ minh họa:
Ví dụ 1:
Nếu hàm số là f(x) = x^2 và tiếp điểm là (1, 1), bạn sẽ làm như sau:
– Tính đạo hàm của hàm số: f'(x) = 2x.
– Tính hệ số góc tại tiếp điểm: f'(1) = 2.
– Viết phương trình tiếp tuyến: y – 1 = 2(x – 1).
Ví dụ 2:
Cho hàm số y = x3. Viết tiếp tuyến của đồ thị hàm số đã cho
a) Biết tiếp điểm là M(1; 1).
b) Biết hoành độ tiếp điểm bằng 2.
c) Biết tung độ tiếp điểm bằng 5.
Lời giải:
Đặt f(x) = x³
Khi đó: f'(x) = 3x²
a) Gọi k là hệ số góc của tiếp tuyến tại M, ta có: k = f'(1) = 3.
Phương trình tiếp tuyến tại M là: y = 3(x – 1) + 1. Hay y = 3x – 2.
b) Gọi M (xM; yM) là tiếp điểm.
Hoành độ tiếp điểm xM = 2 nên tung độ yM = (xM)³ = 8. Vậy M(2; 8).
Gọi k là hệ số góc của tiếp tuyến tại M suy ra k = f'(2) = 12
Phương trình tiếp tuyến tại M là: y = 12(x – 2) + 8. Hay y = 12x – 16.
c) Gọi M (xM; yM) là tiếp điểm.
Tung độ tiếp điểm yM = 5 ⇒ (xM)³ = 5 ⇒ ![]()
Gọi k là hệ số góc của tiếp tuyến tại M ⇒ ![]()
Phương trình tiếp tuyến tại M là: ![]() .
.
2. Dạng bài tập Viết phương trình tiếp tuyến khi biết hệ số góc k:
* Phương pháp giải:
Để viết phương trình tiếp tuyến của đồ thị hàm số tại một điểm khi biết hệ số góc k, bạn có thể làm theo các bước sau:
– Xác định hàm số f(x) mà bạn đang xét.
– Tìm điểm (x0, f(x0)) trên đồ thị mà tại đó bạn muốn viết phương trình tiếp tuyến.
– Sử dụng công thức phương trình tiếp tuyến: y = f(x0) + k. (x – x0), trong đó:
+ y là giá trị của hàm số tại điểm cần tìm.
+ f(x0) là giá trị của hàm số tại x0.
+ k là hệ số góc đã cho.
+ x là biến số.
* Chú ý:
– Cho hai đường thẳng: d1 : y = a1x + b1 và d2 : y = a2x + b2, với a1, a2 lần lượt là hệ số góc của d1 và d2. Khi đó:
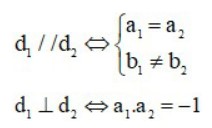
– Hệ số góc của đường thẳng (d) y = ax + b là: kd = a = tanα với α là góc nằm bên trên trục hoành tạo bởi đường thẳng (d) và chiều dương của trục Ox.
Khi a > 0, ta có kd = tanα = a.
Khi a < 0, ta có kd = tan(180° − α).
* Ví dụ minh họa:
Ví dụ 1:
Nếu hàm số là f(x) = x² và bạn muốn tìm phương trình tiếp tuyến tại điểm có hoành độ x0 = 1 với hệ số góc k = 2, bạn sẽ có:
– Tính giá trị của hàm số tại x0: f(1) = 1² = 1.
– Thay các giá trị vào công thức: y = 1 + 2(x – 1).
– Đơn giản hóa phương trình: y = 2x – 1.
Phương trình y = 2x – 1 chính là phương trình tiếp tuyến cần tìm.
Ví dụ 2:
Cho hàm số y = f(x) = ⅓.x³ – ½.x² + 1 có đồ thị (C), viết phương trình tiếp tuyến của (C) biết :
a) Tiếp tuyến có hệ số góc bằng 2.
b) Tiếp tuyến vuông góc với đường thẳng (d): y = – ⅙.x + 1.
c) Tiếp tuyến song song với đường thẳng (d’): y = 2020.
Lời giải:
Ta có y’ = f'(x) = x2 – x.
a) Gọi M (x0;y0) ∈ (C) mà tiếp tuyến của (C) tại M có hệ số góc k = 2
⇒ f'(x0) = 2 ⇔ 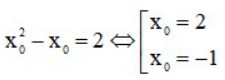
* Với x0 = 2 ta có: y0 = f (0) = ⅓.2³ – ½.2² + 1 = 5/3 => M1 (2;5/3).
Phương trình tiếp tuyến của (C) tại điểm M1 (2;5/3) là y = 2.(x – 2) + 5/3 hay y = 2x – 7/3.
* Với x0 = – 1 ta có y0 = f(-1) = ⅙ => M2 (-1;⅙).
Phương trình tiếp tuyến của (C) tại điểm M2 (-1;⅙) là y = 2(x + 1) + ⅙ hay y = 2x + 13/6.
b) Gọi k là hệ số góc của tiếp tuyến của đồ thị (C)
Do tiếp tuyến vuông góc với (d) y = -⅙.x + 1 nên – ⅙.k = -1 => k = 6.
Gọi M (x0; y0) là điểm thuộc đồ thị (C) mà tiếp tuyến của (C) tại M có hệ số góc k = 6.
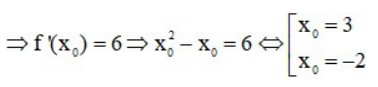
* Với x0 = 3 ta có y0 = f(3) = y0 = f(3) = 11/2 ⇒ M1 (3;11/2) ∈ C.
Phương trình tiếp tuyến của (C) tại M1 (3;11/2) là y = 6(x – 3) + 11/2 hay y = 6x – 25/2.
* Với x0 = – 2 ta có y0 = f(−2) = -11/3⇒ M2 (-2; -11/3) ∈ C.
Phương trình tiếp tuyến của (C) tại M2 (-2; -11/3) là y = 6(x + 2) – 11/3 hay y = 6x + 25/3.
c) Gọi k là hệ số góc của tiếp tuyến của đồ thị (C).
Do tiếp tuyến song song với (d’) : y = 2020 với hệ số góc
⇒ k = 0
Gọi M (x0; y0) là điểm thuộc đồ thị (C) mà tiếp tuyến của (C) tại M có hệ số góc k = 0 .
⇒ f'(x0) = 0 ⇔ 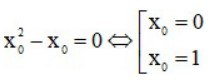
* Với x0 = 0 ta có y0 = f(0) = 1 ⇒ M1(0;1) ∈ (C).
Phương trình tiếp tuyến của (C) tại M1(0; 1) là y = 1.
* Với x0 = 1 ta có y0 = f(1) = ⅚ => M2 (1;⅚) ∈ (C).
Phương trình tiếp tuyến của (C) tại M2 (1;⅚) là y = ⅚.
3. Dạng bài tập Viết phương trình tiếp tuyến khi biết tiếp tuyến đi qua một điểm cho trước:
* Phương pháp giải:
Để viết phương trình tiếp tuyến của đồ thị hàm số tại một điểm cho trước, bạn cần thực hiện các bước sau:
– Xác định hàm số của đồ thị mà bạn đang xét. Ví dụ: f(x) = x².
– Tìm tọa độ của điểm mà tiếp tuyến sẽ đi qua. Giả sử điểm đó có tọa độ là (x0, y0).
– Tính đạo hàm của hàm số tại điểm x0 để tìm hệ số góc của tiếp tuyến. Ví dụ: f'(x0) .
– Sử dụng công thức của phương trình tiếp tuyến: y – y0 = f'(x0)(x – x0).
– Thay các giá trị đã tìm được vào công thức để có phương trình tiếp tuyến cụ thể.
* Ví dụ minh họa:
Ví dụ 1:
Cho hàm số là ( f(x) = x^2 ) và điểm cho trước là ( (2, 4) ), chúng ta có:
– Tính đạo hàm của hàm số: f'(x) = 2x.
– Tính đạo hàm tại điểm x0 = 2: f'(2) = 4.
– Viết phương trình tiếp tuyến: y – 4 = 4(x – 2).
Kết quả, phương trình tiếp tuyến là y = 4x – 4.
Ví dụ 2:
Cho hàm số y = 4×3 – 6×2 + 1. Viết phương trình tiếp tuyến với đồ thị hàm số biết tiếp tuyến qua điểm M(– 1; – 9).
Lời giải:
Gọi A (x0: 4×0³ – 6×0² + 1) là tiếp điểm của của tiếp tuyến và đồ thị hàm số.
f'(x) = 12×2 – 12x.
Ta có phương trình tiếp tuyến của đồ thị hàm số tại A là
d: y = (12×0² – 12×0) . (x – x0) + 4×0³ – 6×0² + 1.
Vì M ∈ d nên: -9 = (12×0² – 12×0) . (-1 – x0) + 4×0³ -6×0² + 1.
⇔-8×0³ – 6×0² + 12x⁰ + 10 =0 ⇔ 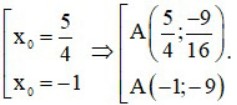
Với A (5/4; -9/16), ta có phương trình tiếp tuyến là: y = 15/4x – 21/16.
Với A (−1;−9), ta có phương trình tiếp tuyến là: y = 24x + 15.
THAM KHẢO THÊM: