Trong toán học, Nguyên hàm là một khái niệm quan trọng và thường được sử dụng trong việc tính diện tích dưới đồ thị của một hàm số. Để giúp bạn hiểu rõ hơn về nguyên hàm và cách giải các dạng bài tập liên quan, dưới đây là một số ví dụ thường gặp và cách giải chúng.
Mục lục bài viết
1. Định nghĩa, công thức Nguyên hàm:
Định nghĩa:
Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.
Kí hiệu: ∫ f(x)dx = F(x) + C.
Định lí 1:
Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng: F(x) + C với C là một hằng số.
Hơn nữa, ta có thể chứng minh rằng họ tất cả các nguyên hàm của f(x) trên K cũng có dạng: F(x) + C với C là một hằng số bất kỳ. Điều này có nghĩa là mọi nguyên hàm của hàm số f(x) trên K đều thuộc vào họ tất cả các nguyên hàm F(x) + C.
Đặc biệt, nếu ta lấy C = 0, ta có nguyên hàm duy nhất của f(x) trên K là: F(x) + 0 = F(x).
Hơn nữa, hàm số F(x) + C là một họ tất cả các nguyên hàm của f(x) trên K, với C là một hằng số trong tập số thực R. Từ đó, ta có thể hiểu rằng hàm số F(x) + C là một tập hợp không thể đếm được các nguyên hàm của f(x) trên K, với mỗi hằng số C tương ứng với một nguyên hàm khác nhau.
Vậy, F(x) + C; C ∈ R là họ tất cả các nguyên hàm của f(x) trên K.
Tính chất của nguyên hàm:
(∫ f(x)dx)’ = f(x) và ∫ f'(x)dx = f(x) + C.
Nếu F(x) có đạo hàm thì: ∫d(F(x)) = F(x) + C).
∫kf(x)dx = k∫ f(x)dx với k là hằng số khác 0.
∫[f(x) ± g(x)]dx = ∫ f(x)dx ± ∫g(x)dx.
Sự tồn tại của nguyên hàm
Định lí về sự tồn tại của nguyên hàm:
Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
Ví dụ về tính chất của nguyên hàm:
∫ f(x)dx)’ = f(x) là tính chất quan trọng của nguyên hàm. Điều này có nghĩa là đạo hàm của một nguyên hàm chính là hàm gốc.
∫ kf(x)dx = k∫ f(x)dx là tính chất của nguyên hàm khi nhân một hàm số với một hằng số.
∫[f(x) ± g(x)]dx = ∫ f(x)dx ± ∫g(x)dx là tính chất của nguyên hàm khi tính toán tổng hoặc hiệu của hai hàm số.
Ứng dụng của nguyên hàm:
Nguyên hàm được sử dụng trong tính toán diện tích dưới đường cong của một hàm số. Bằng cách tính nguyên hàm của hàm số và tính giá trị tại hai điểm xác định, ta có thể tính diện tích dưới đường cong.
Nguyên hàm cũng được sử dụng trong việc tính toán tổng lượng thay đổi của một đại lượng theo thời gian.
2. Bảng nguyên hàm thường gặp:
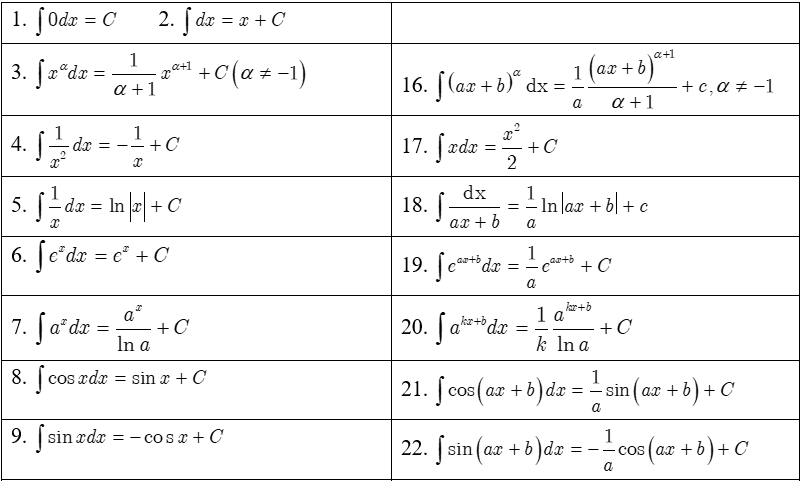
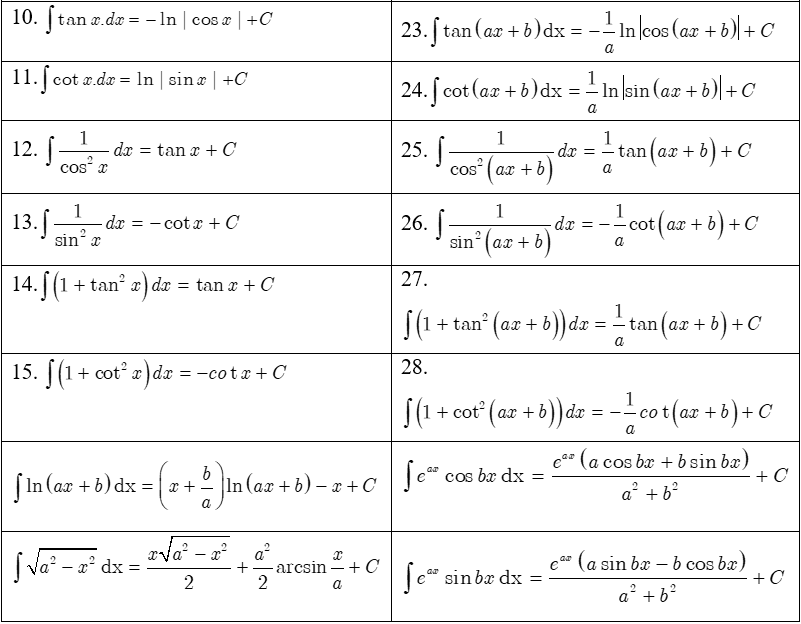
3. Các dạng bài tập nguyên hàm:
Dạng 1: Tìm nguyên hàm của hàm số
Phương pháp sử dụng định nghĩa và tính chất
Để tìm nguyên hàm của một hàm số, chúng ta có thể áp dụng các bước sau:
Biến đổi hàm số dưới dấu nguyên hàm thành dạng tổng hoặc hiệu của các biểu thức chứa biến x. Điều này giúp chúng ta phân rã hàm số ban đầu thành những phần nhỏ hơn, dễ dàng tính toán hơn.
Chuyển đổi mỗi biểu thức chứa biến x vào dạng cơ bản có sẵn trong bảng nguyên hàm. Bảng nguyên hàm cung cấp cho chúng ta các công thức nguyên hàm căn bản của các biểu thức phổ biến như hằng số, biến mũ, hàm lượng giác, và nhiều hơn nữa.
Sử dụng các công thức nguyên hàm cơ bản có trong bảng để tính toán nguyên hàm của các biểu thức đã chuyển đổi. Bằng cách áp dụng các công thức nguyên hàm, chúng ta có thể tính toán giá trị của từng phần tử trong dạng tổng hoặc hiệu và kết hợp chúng lại để tạo thành nguyên hàm của hàm số ban đầu.
Qua quá trình này, chúng ta sẽ có thể tìm được nguyên hàm của hàm số ban đầu và giải quyết các bài toán liên quan đến tích phân trong toán học và vật lý.
Dạng 2: Để tìm nguyên hàm bằng phương pháp đổi biến số, ta thực hiện các bước sau đây:
Chọn một biến số mới để thay thế biến số ban đầu trong biểu thức cần tích phân.
Thay thế biến số ban đầu bằng biến số mới trong toàn bộ biểu thức.
Tính đạo hàm của biến số mới theo biến số ban đầu.
Thay thế lại biến số mới bằng biến số ban đầu trong biểu thức đạo hàm.
Giải tích phân của biểu thức đạo hàm theo biến số ban đầu.
Thay thế biến số ban đầu bằng biến số mới trong kết quả cuối cùng để thu được nguyên hàm.

Dạng 3: Phương pháp tìm nguyên hàm bằng phương pháp từng phần
Khi đối mặt với bài toán tìm nguyên hàm của các hàm số dạng tích (hoặc thương) của hai hàm số “khác lớp hàm”, chúng ta thường áp dụng phương pháp tìm nguyên hàm từng phần theo công thức đã biết.
Phương pháp này giúp chúng ta phân rã bài toán phức tạp thành các phần nhỏ hơn, từ đó giúp dễ dàng xác định nguyên hàm của từng phần đó.
Việc sử dụng phương pháp nguyên hàm từng phần mang lại sự thuận tiện và linh hoạt trong việc giải quyết các bài toán liên quan đến nguyên hàm của các hàm số dạng tích hoặc thương.
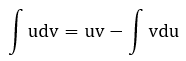
Dưới đây là một số trường hợp thường gặp như thế (với P(x) là một đa thức theo ẩn x). Hãy xem xét một số ví dụ cụ thể để hiểu rõ hơn về khái niệm này.
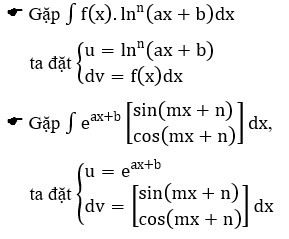
Dạng 4: Tìm nguyên hàm của số hữu tỉ
Ngoài những quy tắc trên, còn có một số quy tắc khác mà chúng ta có thể áp dụng trong việc tìm nguyên hàm của số hữu tỉ. Ví dụ:
Khi mẫu số Q(x) là một hàm số bất khác 0, ta có thể sử dụng quy tắc đặt một hằng số ở trước tử số và tính nguyên hàm của tử số đó.
Khi tử số P(x) là một hàm số đơn giản như một hàm số bất khác 0, ta có thể sử dụng quy tắc tích một hằng số và tính nguyên hàm của tử số đó.
Nếu tử số P(x) là một hàm số không đóng góp vào việc tìm nguyên hàm của số hữu tỉ, ta có thể bỏ qua tử số đó và tính nguyên hàm của mẫu số Q(x) một cách riêng biệt.
Thêm vào đó, chúng ta có thể sử dụng các công thức đặt quy tắc cho các loại hàm số như hàm mũ, hàm lôgarit, hàm căn, và các quy tắc đặt một hàm số đặc biệt như hàm số mũ, hàm số sỉ, và hàm số tam giác.
Dạng 5: Tìm nguyên hàm thoả mãn điều kiện cho trước
Bước 1: Để tìm nguyên hàm của một hàm số, chúng ta có thể sử dụng những phương pháp đã biết như bảng nguyên hàm, đổi biến số và tính nguyên hàm từng phần. Sử dụng bảng nguyên hàm giúp chúng ta tìm được nguyên hàm ban đầu của một hàm số dễ dàng hơn. Đổi biến số cũng là một phương pháp hữu ích để chuyển đổi hàm số ban đầu thành một dạng mà chúng ta có thể tính nguyên hàm dễ dàng hơn. Ngoài ra, tính nguyên hàm từng phần cũng là một phương pháp khá phổ biến để tìm nguyên hàm của một hàm số phức tạp.
Bước 2: Sau khi tìm được nguyên hàm ban đầu, chúng ta cần dựa vào yêu cầu của bài toán để tìm ra hằng số C phù hợp. Hằng số C thường được xác định bởi các điều kiện ban đầu hoặc các ràng buộc khác trong bài toán.
Bước 3: Cuối cùng, chúng ta kết luận một nguyên hàm đã tìm được thông qua quá trình tính toán và áp dụng các phương pháp trên.
Tóm lại, nguyên hàm là dạng toán phổ biến và được ứng dụng rất nhiều trong toan học và trong các kỳ thi.




