Các bước so sánh hai phân số dễ hiểu nhất Toán lớp 4

1. Các bước so sánh hai phân số dễ hiểu nhất Toán lớp 4:

Trong học toán, việc so sánh hai phân số là một khía cạnh quan trọng giúp chúng ta đánh giá sự lớn hay nhỏ của chúng và từ đó, áp dụng vào nhiều bối cảnh thực tế. Để thực hiện công việc này một cách chính xác, có nhiều phương pháp, nhưng chúng ta sẽ tập trung vào phương pháp quy đồng tử số, một trong những cách tiếp cận phổ biến và hiệu quả.

So sánh hai phân số là quá trình xác định xem phân số nào lớn hơn, nhỏ hơn hoặc bằng nhau. Trong ngữ cảnh này, chúng ta thường gặp phân số với mẫu số và tử số khác nhau, và điều này làm tăng độ phức tạp trong quá trình so sánh.

Phân số nào có tử số bé hơn thì phân số đó bé hơn:

Ví dụ: So sánh phân số 2/5 và 3/5. Vì mẫu số là 5 (giống nhau), nên chúng ta chỉ cần so sánh tử số. 2/5 có tử số là 2, còn 3/5 có tử số là 3. Do đó, 2/5 bé hơn 3/5.

Phân số nào có tử số lớn hơn thì phân số đó lớn hơn:

Ví dụ: So sánh phân số 4/7 và 2/7. Vì mẫu số là 7 (giống nhau), nên chúng ta so sánh tử số. 4/7 có tử số là 4, còn 2/7 có tử số là 2. Vì vậy, 4/7 lớn hơn 2/7.

Nếu tử số bằng nhau thì hai phân số đó bằng nhau:

Ví dụ: So sánh phân số 3/8 và 3/8. Vì cả hai phân số đều có tử số là 3 và mẫu số là 8, nên chúng bằng nhau.

Bằng cách này, học sinh có thể dễ dàng nhớ những quy tắc đơn giản và áp dụng chúng khi so sánh các phân số. Việc sử dụng ví dụ cụ thể giúp họ thấy minh họa và thực tế hóa khái niệm.

2. So sánh các phân số cùng tử số:

Phân số nào có mẫu số bé hơn thì phân số đó lớn hơn:

Ví dụ: So sánh 2/5 và 2/7. Vì cả hai phân số có tử số giống nhau là 2, chúng ta chỉ cần xem xét mẫu số. 2/5 có mẫu số là 5, còn 2/7 có mẫu số là 7. Theo quy tắc, phân số 2/5 lớn hơn 2/7 vì mẫu số của nó bé hơn.

Phân số nào có mẫu số lớn hơn thì phân số đó bé hơn:

Ví dụ: So sánh 3/8 và 3/6. Vì cả hai phân số có tử số giống nhau là 3, ta chỉ cần xem xét mẫu số. 3/8 có mẫu số là 8, còn 3/6 có mẫu số là 6. Dựa vào quy tắc, phân số 3/8 bé hơn 3/6 vì mẫu số của nó lớn hơn.

Nếu mẫu số bằng nhau thì hai phân số đó bằng nhau:

Ví dụ: So sánh 4/9 và 5/9. Vì cả hai phân số có mẫu số giống nhau là 9, nên chúng bằng nhau theo quy tắc.

Bằng cách sử dụng những ví dụ cụ thể và thực tế, học sinh có thể áp dụng quy tắc một cách hiệu quả hơn. Đồng thời, việc lưu ý đến khả năng nhầm lẫn giữa các quy tắc so sánh cùng tử số cũng là một phần quan trọng giúp họ duy trì sự chính xác khi giải các bài tập toán.

3. So sánh các phân số khác mẫu:

Quy đồng mẫu số

Để so sánh các phân số khác mẫu số, quy đồng mẫu số là một phương pháp quan trọng giúp làm cho so sánh trở nên dễ dàng hơn và chính xác hơn. Hãy mở rộng phương pháp này và cung cấp ví dụ cụ thể để giúp học sinh hiểu rõ hơn.

Ví dụ: So sánh 2/3 và 5/8

Bước 1: Quy đồng mẫu số

Chúng ta cần tìm một mẫu số chung của 3 và 8, tức là bội số chung nhỏ nhất của 3 và 8. Trong trường hợp này, mẫu số chung nhỏ nhất là 24.

2/3 sẽ được nhân với 8/8​ để có cùng mẫu số:

2/3 × 8/8= 16/24​

5/8​ sẽ được nhân với 3/3​ để có cùng mẫu số:

5/8 × 3/3 = 15/24​

Bước 2: So sánh các phân số mới

Bây giờ, chúng ta có 16/24 và 15/24 với cùng mẫu số. Ta chỉ cần so sánh tử số:

16/24 có tử số lớn hơn 15/24.

Bước 3: Rút ra kết luận

2/3​ lớn hơn 5/8​ khi so sánh với cùng mẫu số.

Quy đồng tử số

Khi chúng ta đối mặt với trường hợp hai phân số có mẫu số khác nhau, đặc biệt là khi mẫu số rất lớn và tử số nhỏ, việc quy đồng tử số là một phương pháp hữu ích để giúp làm cho so sánh trở nên thuận tiện và dễ dàng hơn. Chúng ta hãy mở rộng cách tiếp cận này và thêm vào đó những ví dụ cụ thể để làm cho nó trở nên rõ ràng và áp dụng được trong thực tế. 

Quy đồng tử số không chỉ là một phương pháp toán học, mà còn mang lại ý nghĩa trong thực tế. Trong cuộc sống hàng ngày, chúng ta thường phải so sánh các lựa chọn, từ việc mua sắm với giá giảm giá đến việc quyết định thời gian dành cho các hoạt động khác nhau. Việc hiểu cách so sánh giữa các phân số giúp chúng ta ra quyết định một cách thông minh và logic.

Ví dụ: So sánh 1/100 và 2/150​

Bước 1: Quy đồng tử số

Chúng ta muốn có một tử số chung cho cả hai phân số. Trong trường hợp này, bội số chung nhỏ nhất của 100 và 150 là 300.

1/100​ sẽ được nhân với 3/3​ để có cùng tử số:

1/100 × 3/3 ​= 3/300​​

2/150​ sẽ được nhân với 2/2 để có cùng tử số:

2/150 × 2/2 = 4/300​

Bước 2: So sánh tử số

Bây giờ, chúng ta có 3/300​ và 4/300 với cùng tử số. Chỉ cần so sánh mẫu số:

3/300có mẫu số nhỏ hơn 4/300

Bước 3: Rút ra kết luận

1/100 bé hơn 2/150 khi so sánh với cùng tử số.

Ưu điểm của phương pháp này:

1. Dễ áp dụng: Quy đồng tử số giúp đơn giản hóa quá trình so sánh, đặc biệt là khi có sự chênh lệch lớn giữa các mẫu số.

2. Hiệu quả tính toán: Việc chọn bội số chung nhỏ nhất giúp giảm thiểu sự phức tạp trong tính toán.

3. Hiểu quả trong thực tế: Phương pháp này thường được sử dụng trong các bài toán thực tế khi các mẫu số không thể dễ dàng đồng nhất.

So sánh hai phân số là một kỹ năng quan trọng, giúp chúng ta hiểu rõ hơn về mối quan hệ giữa chúng và áp dụng vào nhiều tình huống thực tế. Phương pháp quy đồng tử số đơn giản và hiệu quả, mang lại giá trị lớn trong quá trình giảng dạy và học tập toán học.

Nhìn chung, việc nắm vững cách so sánh hai phân số không chỉ là một kỹ năng toán học, mà còn là một kỹ năng sống quan trọng, giúp chúng ta đưa ra các quyết định thông minh và có logic trong cuộc sống hàng ngày.

4. Giải bài tập So sánh hai phân số:

Bài 1: So sánh hai phân số:

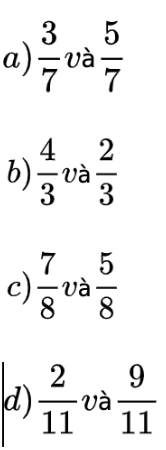
Hướng dẫn giải:

Trong hai phân số cùng mẫu số:

– Phân số nào có tử số bé hơn thì bé hơn.

– Phân số nào có tử số lớn hơn thì lớn hơn.

– Nếu tử số bằng nhau thì hai phân số đó bằng nhau.

Đáp án:

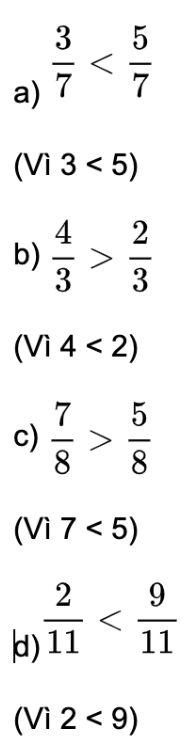
Bài 2:

a) Nhận xét:

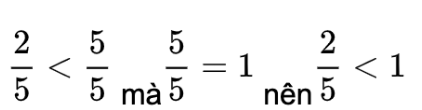
Nếu tử số bé hơn mẫu số thì phân số đó bé hơn 1

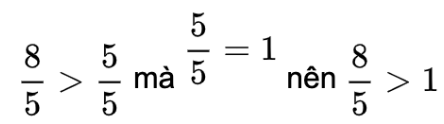
Nếu tử số lớn hơn mẫu số thì phân số đó lớn hơn 1.

b) So sánh các phân số sau với 1:

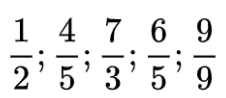
Hướng dẫn giải:

– Phân số có tử số bé hơn mẫu số thì phân số bé hơn 1.

– Phân số có tử số lớn hơn mẫu số thì phân số lớn hơn 1.

– Phân số có tử số bằng mẫu số thì phân số bằng 1.

Đáp án:

Ta có kết quả lần lượt như sau:

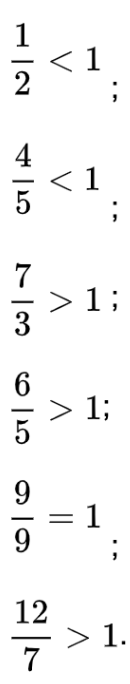
Bài 3:

Viết các phân số bé hơn 1, có mẫu số là 5 và tử số khác 0.

Hướng dẫn giải

Phân số có tử số bé hơn mẫu số thì phân số bé hơn 1.

Đáp án:

Các phân số bé hơn 1, có mẫu số là 5 và tử số khác 0 là:

.

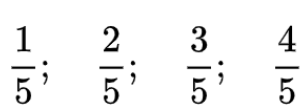
Bài 4:

Viết các phân số 4/7, 3/7/ 6/7 theo thứ tự từ bé đến lớn.

Phương pháp giải:

– So sánh các phân số rồi sắp xếp theo thứ tự từ bé đến lớn.

– Áp dụng cách so sánh hai phân số cùng mẫu số:

Trong hai phân số cùng mẫu số :

+ Phân số nào có tử số bé hơn thì bé hơn.

+ Phân số nào có tử số lớn hơn thì lớn hơn.

+ Nếu tử số bằng nhau thì hai phân số đó bằng nhau.

Đáp án