Bài tập về vị trí tương đối của đường thẳng và đường tròn

04/09/202404/09/2024

04/09/2024

Bài viết dưới đây cung cấp cho các bạn học sinh các dạng bài tập về vị trí tương đối của đường thẳng và đường tròn để giúp các bạn có thể tự luyện tập và thu nạp thêm được nhiều kiến thức của lĩnh vực này.

Mục lục bài viết

1 1. Lý thuyết:

2 2. Các dạng bài tập:

2.1 2.1. Dạng 1: Cho biết bán kính đường tròn và khoảng cách từ tâm đến đường thẳng, xác định vị trí tương đối của đường thẳng và đường tròn:
2.2 2.2. Dạng 2: Xác định vị trí tâm đường tròn có bán kính cho trước và tiếp xúc với một đường thẳng cho trước:
2.3 2.3. Dạng 3: Bài toán liên quan đến tính độ dài:

3 3. Bài tập tự luyện:

1. Lý thuyết:

Cho đường thẳng $Δ”> Δ$ và đường tròn (O; R). Gọi OH là khoảng cách từ tâm O đến đường thẳng $Δ”> Δ$ . Ta có ba vị trí tương đối của đường thẳng và đường tròn như sau:

Trường hợp 1: Nếu $Δ”> Δ$ không cắt (O) thì OH > R ; $Δ”> Δ$ và (O) không có điểm chung. Ta nói đường thẳng ∆ và đường tròn (O) không giao nhau.

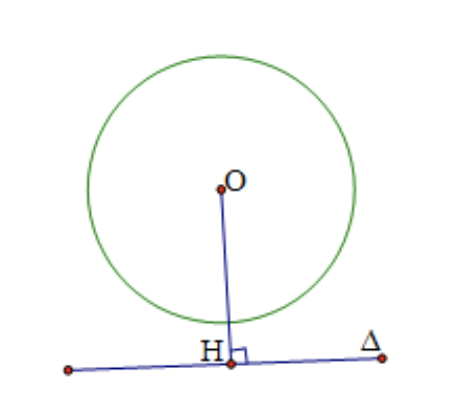
Trường hợp 2: Nếu $Δ”> Δ$ và (O) tiếp xúc nhau thì OH = R; $Δ”> Δ$ và (O) có một điểm chung. Điểm chung đó là H. Khi đó, $Δ”> Δ$ là tiếp tuyết của đường tròn (O).

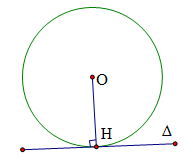
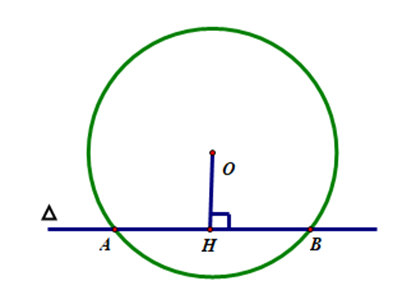
Trường hợp 3: Nếu $Δ”> Δ$ và (O) cắt nhau thì OH < R; $Δ”> Δ$ và (O) có hai điểm chung là A và B. Khi đó, ta gọi đường thẳng $Δ”> Δ$ là cát tuyến của đường tròn (O).

2. Các dạng bài tập:

2.1. Dạng 1: Cho biết bán kính đường tròn và khoảng cách từ tâm đến đường thẳng, xác định vị trí tương đối của đường thẳng và đường tròn:

Phương pháp giải: Gọi khoảng cách từ tâm đường tròn đến đường thẳng là d; bán kính là R ta so sánh d với R rồi dựa vào kiến thức về vị trí tương đối của đường thẳng và đường tròn để kết luận.

– Nếu d > R thù đường thẳng và đường tròn không cắt nhau.

– Nếu d = R thì đường thẳng và đường tròn tiếp xúc nhau.

– Nếu d < R thì đường thẳng và đường tròn cắt nhau.

Ví dụ : Cho điểm B(2;4). Hãy xác định vị trí tương đối của đường tròn (B; 3) với hai trục Ox; Oy.

Lời giải:

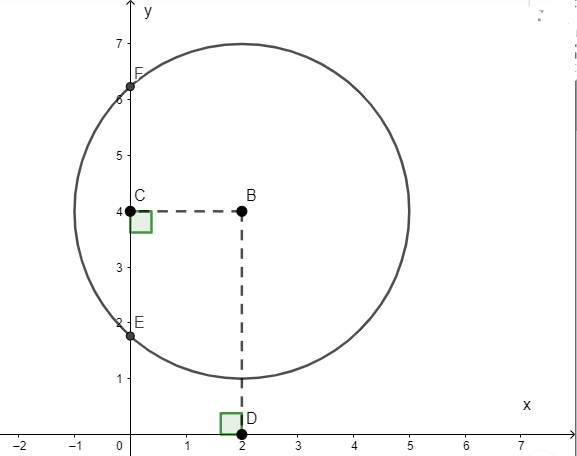
Vẽ BC $⊥”> ⊥$ Oy $\Rightarrow”> \Rightarrow$ BC = 2

Vẽ BD $⊥”> ⊥$ Ox $\Rightarrow”> \Rightarrow$ BD = 4

Vì BC < R (2 < 3) nên đường tròn cắt trục Oy tại hai điểm E và F hay (B) cắt trục Oy

Vì BD > R (4 > 3) nên đường tròn và trục Ox không có điểm chung hay (B) và Ox không cắt nhau.

2.2. Dạng 2: Xác định vị trí tâm đường tròn có bán kính cho trước và tiếp xúc với một đường thẳng cho trước:

Phương pháp giải: Xác định khoảng cách từ tâm đường tròn đến đường thẳng cho trước rồi sử dụng tính chất điểm cách đều một đường thẳng cho trước một khoảng cách không đổi.

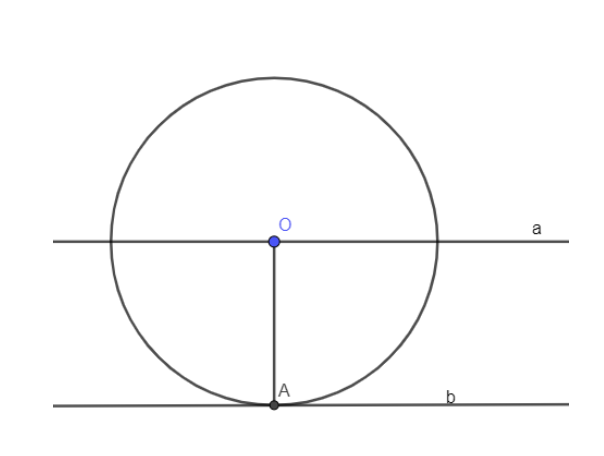
Ví dụ 1: Cho hai đường thẳng a và b song song với nhau cách nhau một khoảng là 4cm. Lấy điểm O trên a vẽ đường tròn (O; 4cm). Chứng minh O tiếp xúc với b.

Lời giải:

Vì O $\in”> \in$ a nên O cũng cách b một khoảng 4cm.

Mà bán kính đường tròn cũng là 4cm

$\Rightarrow”> \Rightarrow$ (O;4cm) tiếp xúc với b.

Ví dụ 2: Cho hình vuông ABCD. Trên đường chéo BD lấy H sao cho BH = AB. Qua H kẻ đường thẳng vuông góc với BD cắt AD cắt AD tại O.

a) So sánh OA; OH và HD.

b) Xác định vị trí tương đối của BD với (O; OA).

Lời giải:

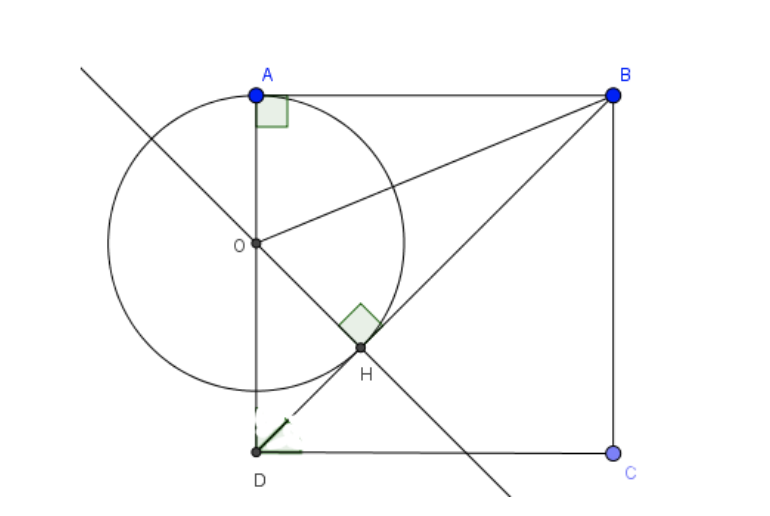
a) Xét $ΔOAB”> Δ O A B$ và $ΔOHB”> Δ$ $ΔOHB”> O$ $ΔOHB”> H B$ có:

OB chung

AB = BH (giả thuyết)

$OAB^=OHB^=90°”> góc O A B = góc O H B = 90 °$

Do đó $ΔOAB”> Δ O A B$ = $ΔOHB”> Δ O H B$ (cạnh huyền – cạnh góc vuông)

$\Rightarrow”> \Rightarrow$ OA = OH (hai cạnh tương ứng) (1)

Xét tam giác OHD vuông tại H có góc $ODH^=45°”> O D H$ $ODH^=45°”> = 45$ $ODH^=45°”> °$ (do BD là đường chéo của hình vuông ABCD)

$\Rightarrow”> \Rightarrow \Rightarrow$ $ΔOHD”> Δ O H D$ là tam giác vuông cân tại H

$\Rightarrow”> \Rightarrow \Rightarrow$ OH = HD (2)

Từ (1) và (2) $\Rightarrow”> \Rightarrow \Rightarrow$ OH = HD = OA

b) Vì OA = OH và OH $⊥”> ⊥$ BD nên BD là tiếp tuyến của đường tròn (O;OA)

Vậy BD tiếp xúc với (O;OA).

2.3. Dạng 3: Bài toán liên quan đến tính độ dài:

Phương pháp giải: Nối tâm với điểm rồi vận dụng định lí về tính chất của tiếp tuyến và định lý Py – ta – go.

Ví dụ 1: Cho đường tròn tâm O bán kính 8cm và một điểm A cách O là 10cm. Kẻ AB là tiếp tuyến, B là tiếp điểm. Tính AB.

Lời giải:

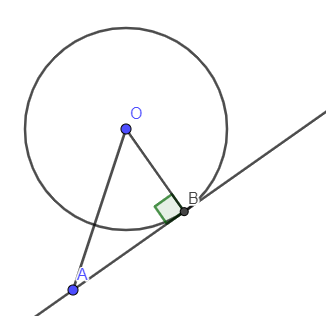
Vì AB là tiếp tuyến của (O), B là tiếp điểm nên AB $⊥”> ⊥$ OB

Xét tam giác OAB vuông tại B ta có:

$OB2+AB2=OA2″> O B^2 + A B OB2+AB2=OA2″>^2 = O A OB2+AB2=OA2″>^2$ (định lý Py – ta – go)

Thay OA = 10cm; OB = 8cm ta có:

$82+AB2=102″> 8 OB2+AB2=OA2″>^2 + A B OB2+AB2=OA2″>^2 = 10 OB2+AB2=OA2″>^2$

$\Leftrightarrow64+AB2=100″> \Leftrightarrow 64 + A B OB2+AB2=OA2″>^2 = 100$

$\LeftrightarrowAB2=100-64″> \Leftrightarrow A B OB2+AB2=OA2″>^2 = 100 - 64$

$\LeftrightarrowAB2=36″> \Leftrightarrow A B OB2+AB2=OA2″>^2 = 36$

$\LeftrightarrowAB=6″> \Leftrightarrow A B = 6$

Vậy AB = 6cm.

Ví dụ 2: Cho đường tròn (O;8), Từ M ngoài (O) vẽ hai tiếp tuyến AM và BM sao cho AM $⊥”> ⊥$ BM tại M với A, B là hai tiếp điểm.

a) Tính AM và BM.

b) Gọi I là giao điểm của OM với (O) (I nằm giữa O và M). Tại I kẻ tiếp tuyến với (O) và cắt OA, OB lần lượt ở C và D. Tính CD.

Lời giải:

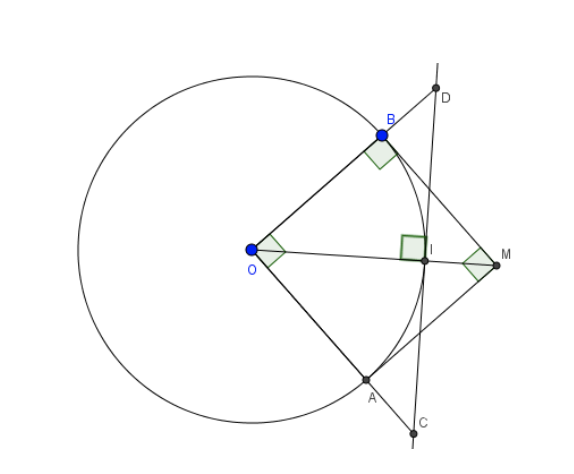
a) Vì A, B là tiếp điểm nên OA $⊥”> ⊥ ⊥$ AM và OB $⊥”> ⊥ ⊥$ BM $\RightarrowOBM^=OAM^=90°”> \Rightarrow góc O B M = góc O A M = 9 0 °$

Lại có: MA $⊥”> ⊥ ⊥$ MB $\RightarrowAMB^=90°”> \Rightarrow góc A M B = 90 °$

Xét tứ giác OBMA có:

$OBM^=OAM^=AMB^=90°”> góc O B M = OBM^=OAM^=AMB^=90°”> góc O A M = OBM^=OAM^=AMB^=90°”> góc A M B = 90 °$

$\Rightarrow”> \Rightarrow$ tứ giác OBMA là hình chữ nhật

Lại có OB = OA = R

Do đó tứ giác OBMA là hình vuông

$\RightarrowOA=OB=MA=MB”> \Rightarrow O A = O B = M A = M B$

Mà OA = OB = R = 8

Nên MA = MB = 8 (đơn vị độ dài)

b) Vì OBMA là hình vuông nên OM là đường phân giác góc O

$\RightarrowAOM^=BOM^=45°”> \Rightarrow góc A O M = góc B O M = 45 °$

Vì CD là tiếp tuyến; I là tiếp điểm nên CD $⊥”> ⊥$ OI

Xét tam giác OIC vuông tại I ta có:

$COI^”> góc C O I$ = $450″> 45 độ$

$\Rightarrow”> \Rightarrow$ tam giác OIC cân tạI I (tính chất)

$\Rightarrow”> \Rightarrow$ IC = IO = R = 8

Xét tam giác OID vuông tại I ta có:

$DOI^”> góc D O I = 450″> 45 độ$

$\Rightarrow”> \Rightarrow$ Tam giác OID cân tại I

$\Rightarrow”> \Rightarrow$ ID = IO = 8

Ta có:

CD = ID + IC = 8 + 8 = 16 (đơn vị độ dài).

3. Bài tập tự luyện:

Phần 1: Trắc nghiệm

Câu 1: Câu nào sau đây là đúng.

A. Đường thẳng tiếp xúc với đường tròn khi đường thẳng có một giao điểm với đường tròn.

B. Đường thẳng cắt đường tròn khi đường thẳng có một giao điểm với đường tròn.

C. Đường thẳng không cắt đường tròn khi khoảng cách từ tâm của đường tròn đến đường thẳng nhỏ hơn bán kính.

D. Khoảng cách từ tâm đường tròn đến đường thẳng nhỏ hơn R thì đường thẳng tiếp xúc với đường tròn.

Câu 2: Cho (O;6cm) và đường thẳng a. Gọi d là khoảng cách từ tâm O đến đường thẳng a. Điều kiện để a cắt O là:

A. Khoảng cách d < 6cm

B. Khoảng cách d = 6cm

C. Khoảng cách d > 6cm

D. Khoảng cách d $\leq”> \leq$ 6cm

Câu 3: Cho điểm A(3;4). Khi đó đường tròn (A;4) sẽ có vị trí như thế nào với hai trục Ox; Oy.

A. Cắt Ox và tiếp xúc với Oy

B. Cắt cả Ox và Oy

C. Cắt Oy và tiếp xúc với Ox

D. Tiếp xúc với Ox và không giao với Oy

Câu 4: Cho đường thẳng d. Tâm các đường tròn có bán kính là 2 và tiếp xúc với d nằm trên đường nào?

A. Một đường thẳng song song với d cách d một khoảng bằng 1cm

B. Một đường thẳng song song với d cách d một khoảng là 2cm

C. Hai đường thẳng song song với d cách d một khoảng là 1cm

D.Hai đường thẳng song song với d cách d một khoảng là 2cm

Phần 2: Tự luận

Bài 1: Trên mặt phẳng tọa độ Oxy cho A(2;5). Vẽ đường tròn (A;3). Xác định vị trí tương đối của (A;3) với hai trục Ox; Oy.

Bài 2: Xác định tâm đường tròn có bán kính 5cm tiếp xúc với đường thẳng d nằm trên đường nào.

Bài 3: Cho đường tròn (O;R) và dây $AB=85R”> A B = 8/ 5 R =85$ , vẽ một tiếp tuyến song song với AB, cắt các tia OA, OB lần lượt tại M và N. Tính diện tích tam giác OMN theo R.

Bài 4: Cho đường tròn (O) đường kính AB = 2R. Bán kính OC vuông góc với AB. Lấy điểm F thuộc đoạn OB. Kẻ CF cắt đường tròn (O) tại D vẽ tiếp tuyến của đường tròn tại D cắt AB tại E.

Chứng minh EF = ED.

Bài 5: Cho điểm A cách đường thẳng xy là 12cm

a) Chứng minh (A;13cm) cắt đường thẳng xy tại hai điểm phân biệt.

b) Gọi giao điểm của (A;13cm) với xy là C và D. Tính độ dài đoạn thẳng CD.

Bài 6: Cho đường tròn (O) đường kính AB. Một điểm M thay đổi trên đường tròn (M khác A và B). Vẽ đường tròn (M) tiếp xúc với AB tại H. Từ A và B kẻ hai tiếp tuyến trên AC, BD đến đường tròn (M)

a) Chứng minh: CD là tiếp tuyến của đường tròn (O).

b) Chứng minh AC + BD không đổi.

c) Tính giá trị lớn nhất của AC.BD.

Bài 7: Cho đường tròn (O;R) đường kính AB. Trên tia đối tia AB lấy điểm C. Từ C kẻ tiếp tuyến CD với (O). Kẻ DH $⊥”> ⊥$ AB tại H

Chứng minh: CH.CO = CA.CB.

Bài 8: Cho nửa đường tròn (O), đường kính AB. Lấy điểm C thuộc (O) và gọi d là tiếp tuyến qua C với (O). Kẻ AE và BF cùng vuông góc với d; CH vuông góc với AB.

a) Chứng minh: CE = CF và $CH2=AE.BF”> C H^2 = A E . B F$

b) Khi C di chuyển trên nửa đường tròn, tìm vị trí của C để EF lớn nhất.

Đáp án trắc nghiệm

Câu 1: A

Câu 2: A

Câu 3: C

Câu 4: D