Bác Ba là người chứng kiến toàn bộ câu chuyện của cha con ông Sáu. Bác Ba đã kể lại truyện Chiếc lược ngà thể hiện cái nhìn khách quan hơn về câu chuyện. Xem bài viết dưới đây về một số mẫu Đóng vai bác Ba kể lại chuyện Chiếc lược ngà hay chọn lọc.
Giáo dục
Giáo dục
Notice: Function wpdb::prepare được gọi không chính xác. Tham số truy vấn của wpdb::prepare() phải có một chỗ chèn. Vui lòng xem Hướng dẫn Debug trong WordPress để biết thêm thông tin. (Thông điệp này đã được thêm vào trong phiên bản 3.9.0.) in /home/luatduong/wp-includes/functions.php on line 6121
Notice: Function wpdb::prepare được gọi không chính xác. Tham số truy vấn của wpdb::prepare() phải có một chỗ chèn. Vui lòng xem Hướng dẫn Debug trong WordPress để biết thêm thông tin. (Thông điệp này đã được thêm vào trong phiên bản 3.9.0.) in /home/luatduong/wp-includes/functions.php on line 6121
Chủ đề liên quan
Bài viết
Tình phụ tử là tình cảm thiêng liêng, dù trong hoàn cảnh gian nan thế nào cũng không thể làm phai nhạt đi tình cảm thiêng liêng đó được, hãy cùng chúng tôi tìm hiểu những bài cảm nhận tình cha con trong tác phẩm Chiếc lược ngà để làm rõ hơn nội dung này nhé
Truyện ngắn “Chiếc lược ngà” được sáng tác năm 1966, ngợi ca tình cha con, tình đồng chí trong cảnh ngộ éo le của chiến tranh. Đồng thời, tác giả cũng muốn tố cáo chiến tranh đã phá hoại biết bao gia đình hạnh phúc. Qua bài văn dưới đây sẽ giúp chúng ta cảm nhận sâu sắc hơn về nhân vật ông Sáu trong truyện ngắn này.
Chiếc lược ngà là một truyện ngắn xuất sắc của nhà văn Nguyễn Quang Sáng về câu chuyện cảm động xoay quanh chiếc lược ngà là kỉ vật duy nhất người cha để lại cho con trước khi hi sinh trên chiến trường. Dưới đây là bài văn mẫu về Đóng vai bé Thu kể lại chuyện Chiếc lược ngà mời bạn đọc theo dõi.
Kết bài của một bài văn không chỉ đơn thuần là kết thúc vấn đề, mà còn là cánh cửa khơi gợi niềm tin yêu, hi vọng cho độc giả. Hôm nay hãy cùng chùng tôi tìm hiểu những mẫu kết bài Chiếc lược ngà của Nguyễn Quang Sáng để thấy được niềm hi vọng của con người về tương lai tươi sáng, vượt qua mất mát đau khổ để tiếp tục phát triển.
Chiếc lược ngà là một trong những tác phẩm nổi bật của nhà văn Nguyễn Quang Sáng với nội dung chủ đề về tình cảm gia đình, sự yêu thương gắn bó của tình thân trong hoàn cảnh chiến tranh chia lìa. Dưới đây là bài viết về chủ đề: Sơ đồ tư duy Chiếc lược ngà ngắn gọn, dễ đọc dễ nhớ, mời bạn đọc theo dõi.
Chiếc lược ngà với các tình huống truyện đầy bất ngờ và hấp dẫn, đã vô cùng thành công trong việc thể hiện tình cảm cha con trong bối cảnh khó khăn của chiến tranh và bom đạn. Dưới đây là Phân tích Chiếc lược ngà của Nguyễn Quang Sáng hay nhất
Để giúp các em có tiết học hiệu quả, hôm nay chúng tôi mang đến cho các em bài soạn Chiếc lược ngà hay nhất, mời các em tham khảo. Đồng thời bài viết cũng giúp các em nhận thức được giá trị hiện thực của tác phẩm, cho chúng ta hi vọng về một tương lai tốt đẹp hơn.
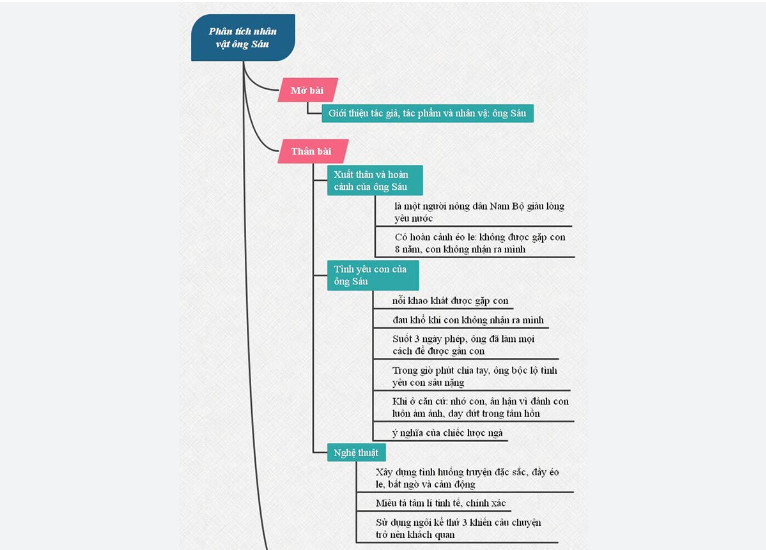
Chiến tranh khốc liệt đã gây ra biết bao thảm kịch cho con người, tình gia đình, cha con, mẫu tử bị chia cắt. Phân tích nhân vật ông Sáu trong Chiếc lược ngà chúng ta sẽ cảm nhận thấy rõ bi kịch đó.
Mở bài là cửa sổ tâm hồn để giúp người ta nhìn thấu nội dung bài đọc, khơi nguồn cảm hứng cho những trang văn tiếp theo. Hôm nay hãy cùng chúng tôi tìm hiểu những mẫu mở bài của bài Chiếc lược ngà qua bài viết dưới đây nhé
Chiếc lược ngà là tác phẩm truyện nổi tiếng của nhà văn Nguyễn Quang Sáng, truyện nói về tình cảm gia đình đặc biệt là tình cha con sâu nặng cao đẹp trong hoàn cảnh chiến tranh khốc liệt. Truyện thành công trong việc tạo dựng tình huống bất ngờ, miêu tả tâm lí nhân vật sâu sắc qua suy nghĩ, hành động. Sau đây là 1 số kiến thức về tác phẩm Chiếc lược ngà, mời các bạn cùng theo dõi!
Truyện ngắn Chiếc lược ngà đã để lại ấn tượng khó phai trong lòng người đọc về tình cảm gia đình trong chiến tranh. Hãy cùng chúng tôi tìm hiểu thêm về tình cảm phụ tử thiêng liêng qua những bài mẫu phân tích tình cảm cha con trong bài Chiếc lược ngà dưới đây nhé
Câu chuyện Chiếc lược ngà của Nguyễn Quang Sáng là câu chuyện cảm động về tình cha con bị chia cắt bởi chiến tranh ác liệt. Bài viết dưới đây sẽ cung cấp những tóm tắt tác phẩm Chiếc lược ngà của Nguyễn Quang Sáng ngắn gọn nhất.
Với giáo án bài Chiếc lược ngà Ngữ văn lớp 9 (tiết 1,2), chuẩn nhất theo mẫu giáo án chuẩn của Bộ GD&ĐT sẽ giúp Giáo viên dễ dàng soạn giáo án Văn 9, từ đó truyền tải tốt hơn thông điệp của tác phẩm đến các em học sinh. Mời các thầy, cô tham khảo trong bài viết dưới đây.
Thông qua tác phẩm Chiếc lược ngà, tác giả Nguyễn Quang Sáng muốn đề cập đến tội ác của chiến tranh và hậu quả với mỗi gia đình. Dưới đây là bài viết về Cảm nhận về nhân vật bé Thu trong Chiếc lược ngà hay nhất.
Chiếc lược ngà là tác phẩm đặc sắc của nhà văn Nguyễn Quang Sáng. Vết sẹo trong tác phẩm là chi tiết quan trọng làm nổi bật lên nội dung của câu chuyện, làm thay đổi tính cách của nhân vật bé Thu. Hãy tham khảo các bài viết phân tích về vết sẹo để có cái nhìn bao quát về câu chuyện.
Truyện ngắn “Chiếc lược ngà” của Nguyễn Quang Sáng là một tác phẩm tiêu biểu của nền văn học Việt Nam và cũng là một trong những tác phẩm về tình cảm gia đình, tình yêu phụ tử để lại những xúc động sâu sắc trong lòng người đọc. Tác phẩm sáng ngời bởi hình ảnh của nhân vật bé Thu – một cô bé vô cùng cá tính, mạnh mẽ và yêu thương ba tha thiết. Dưới đây là bài phân tích về bé Thu trong truyện ngắn “Chiếc lược ngà”.
Tác phẩm Chiếc lược ngà của Nguyễn Quang Sáng đã tái hiện lại tình cảm sâu sắc của hai cha con giữa ông Sáu và bé Thu một cách chân thực nhất dù bị chiến tranh chia cắt. Dưới đây là bài viết cảm nhận đoạn trích Chiếc lược ngà đã được tổng hợp ngắn gọn giúp các bạn hiểu rõ hơn về nội dung, ý nghĩa mà tác phẩm đã mang lại.
Chiếc lược ngà chính là kỉ vật cuối cùng người cha gửi tặng cho con gái trước lúc hi sinh trong kháng chiến chống Mỹ. Chiếc lược ngà ấy thể hiện tình cảm yêu thương, mong nhớ của ông Sáu dành cho con. Để hiểu hơn về hình tượng này, mời các bạn tham khảo bài viết Cảm nhận về ý nghĩa thiêng liêng của chiếc lược ngà dưới đây.
Xem thêm