Phương trình đường thẳng trong không gian là đơn vị kiến thức quan trong chương trình Toán lớp 12. Trong bài viết dưới đây, hãy cùng chúng tôi tìm hiểu về lý thuyết cũng như những bài tập có đáp án về phương trình đường thẳng trong không gian Lớp 12 Bài 3 chính xác nhất.
Mục lục bài viết
- 1 1. Lý thuyết phương trình đường thẳng trong không gian Lớp 12 Bài 3:
- 2 2. Các dạng toán phương trình đường thẳng trong không gian thường gặp:
- 3 3. Những mẹo giúp làm bài tập phương trình đường thẳng trong không gian hiệu quả:
- 4 4. Bài tập trắc nghiệm phương trình đường thẳng trong không gian Lớp 12 Bài 3 chọn lọc hay nhất:
1. Lý thuyết phương trình đường thẳng trong không gian Lớp 12 Bài 3:
1.1. Phương trình đường thẳng:
Cho đường thẳng Δ đi qua điểm Mo(xo; yo; zo) và nhận vectơ a→ = (a1; a2; a3) với a12 + a22 + a32 ≠ 0 làm vectơ chỉ phương. Khi đó Δ có phương trình tham số là :
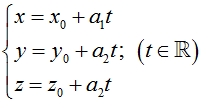
Cho đường thẳng Δ đi qua điểm Mo(xo; yo; zo) và nhận vectơ a→ = (a1; a2; a3) sao cho a1a2a3 ≠ 0 làm vectơ chỉ phương. Khi đó Δ có phương trình chính tắc là :
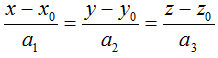
1.2. Góc:
*Góc giữa hai đường thẳng:
Δ1 có vectơ chỉ phương a1→
Δ2 có vectơ chỉ phương a2→
Gọi φ là góc giữa hai đường thẳng Δ1 và Δ2. Ta có:
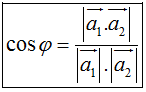
*Góc giữa đường thẳng và mặt phẳng:
Δ có vectơ chỉ phương aΔ→
(α) có vectơ chỉ phương nα→
Gọi φ là góc giữa hai đường thẳng Δ và α. Ta có:
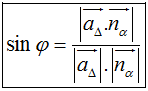
1.3. Khoảng cách:
*Khoảng cách từ điểm M đến đường thẳng Δ:
Δ đi qua điểm Mo và có vectơ chỉ phương aΔ→
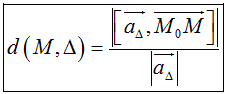
*Khoảng cách giữa hai đường thẳng chéo nhau:
Δ1 đi qua điểm M và có vectơ chỉ phươnga1→
Δ2 đi qua điểm N và có vectơ chỉ phương a2→
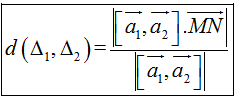
2. Các dạng toán phương trình đường thẳng trong không gian thường gặp:
* Viết phương trình đường thẳng Δ đi qua hai điểm phân biệt A, B.
Cách giải: Xác định vectơ chỉ phương của Δ là AB→.
* Đường thẳng Δ đi qua điểm M và song song với d.
Cách giải:
Trong trường hợp đặc biệt:
+ Nếu Δ song song hoặc trùng bới trục Ox thì Δ có vectơ chỉ phương là aΔ→ = i→ = (1; 0; 0)
+ Nếu Δ song song hoặc trùng bới trục Oy thì Δ có vectơ chỉ phương là aΔ→ = j→ = (0; 1; 0)
+ Nếu Δ song song hoặc trùng bới trục Oz thì Δ có vectơ chỉ phương là aΔ→ = k→ = (0; 1; 0)
Các trường hợp khác thì Δ có vectơ chỉ phương là aΔ→ = ad→, với ad→ là vectơ chỉ phương của d
* Viết phương trình đường thẳng Δ đi qua điểm M và vuông góc với mặt phẳng (α).
Cách giải: Xác định vectơ chỉ phương của Δ là aΔ→ = nα→, với nα→ là vectơ pháp tuyến của (α).
* Viết phương trình đường thẳng Δ đi qua điểm M và vuông góc với hai đường thẳng d1, d2 (hai đường thẳng không cùng phương).
Cách giải: Xác định vectơ chỉ phương của Δ là aΔ→ = [a1→, a2], với a1→, a2→ lần lượt là vectơ chỉ phương của d1, d2.
* Viết phương trình đường thẳng Δ đi qua điểm M vuông góc với đường thẳng d và song song với mặt phẳng (α).
Cách giải:
Xác định vectơ chỉ phương của Δ là aα→ = [ad→, nα→], với ad→ là vectơ chỉ phương của d, nα→ là vectơ pháp tuyến của (α).
* Viết phương trình đường thẳng Δ đi qua điểm A và song song với hai mặt phẳng (α), (β); ((α), (β) là hai mặt phẳng cắt nhau)
Cách giải: Xác định vectơ chỉ phương của Δ là aΔ→ = [nα→, nβ→], với nα→, nβ→ lần lượt là vectơ pháp tuyến của (α), (β).
* Viết phương trình đường thẳng Δ là giao tuyến của hai mặt phẳng (α) và (β).
Cách giải:
– Lấy một điểm bất kì trên Δ, bằng cách cho một ẩn bằng một số tùy ý.
– Xác định vectơ chỉ phương của Δ là aΔ→ = [nα→, nβ→], với nα→, nβ→ lần lượt là vectơ pháp tuyến của (α), (β).
*Viết phương trình đường thẳng Δ đi qua điểm A và cắt hai đường thẳng d1, d2 (A ∉ d1, A ∉ d2).
Cách giải: Xác định vectơ chỉ phương của Δ là aΔ→ = [n1→, n2→], với n1→, n2→ lần lượt là vectơ pháp tuyến của mp(A, d1), mp(A, d2).
*Viết phương trình đường thẳng Δ nằm trong mặt phẳng (α) và cắt hai đường thẳng d1, d2.
Cách giải: Xác định vectơ chỉ phương của Δ là aΔ→ = AB→, với A = d1 ∩ (α), B = d2 ∩ (α)
*Viết phương trình đường thẳng Δ đi qua điểm A, vuông góc và cắt d.
Cách giải:
– Xác định B = Δ ∩ d.
– Viết phương trình đường thẳng Δ đi qua A, B.
*Viết phương trình đường thẳng Δ đi qua điểm A, vuông góc với d1 và cắt d2, với A ∉ d2.
Cách giải:
– Xác định B = Δ ∩ d2.
– Viết phương trình đường thẳng Δ đi qua A, B.
* Viết phương trình đường thẳng Δ đi qua điểm A, cắt đường thẳng d và song song với mặt phẳng (α).
Cách giải:
– Xác định B = Δ ∩ d.
– Viết phương trình đường thẳng Δ đi qua A, B.
*Viết phương trình đường thẳng Δ nằm trong mặt phẳng (α) cắt và vuông góc đường thẳng d.
Cách giải:
– Xác định A = d ∩ (α).
– Đường thẳng Δ đi qua A và có vectơ chỉ phương của Δ là aΔ→ = [ad→, nα→], với ad→ là vectơ chỉ phương của d, nα→ là vectơ pháp tuyến của (α).
* Viết phương trình đường thẳng Δ đi qua giao điểm A của đường thẳng d và mặt phẳng (α), nằm trong (α) và vuông góc đường thẳng d (ở đây d không vuông góc với (α)) .
Cách giải:
– Xác định A = d ∩ (α).
– Đường thẳng Δ đi qua A và có vectơ chỉ phương của Δ là aΔ→ = [ad→, nα→], với ad→ là vectơ chỉ phương của d, nα→ là vectơ pháp tuyến của (α).
3. Những mẹo giúp làm bài tập phương trình đường thẳng trong không gian hiệu quả:
Làm bài tập về phương trình đường thẳng trong không gian là một phần quan trọng trong chương trình Toán lớp 12. Dưới đây là một số mẹo giúp bạn làm bài tập này hiệu quả:
– Hiểu rõ khái niệm và công thức: Trước hết, hãy đảm bảo bạn đã hiểu rõ về định nghĩa và các công thức liên quan đến phương trình đường thẳng trong không gian, bao gồm phương trình chính tắc, phương trình tham số, phương trình tổng quát, và các dạng biểu diễn khác của đường thẳng.
– Xác định điểm và hướng vector: Khi được cho một phương trình đường thẳng, hãy xác định điểm nào thuộc đường thẳng và vector hướng của đường thẳng. Điều này giúp bạn dễ dàng diễn giải và vẽ đường thẳng.
– Sử dụng các phương pháp biểu diễn khác nhau: Khi làm bài tập, sử dụng các biểu diễn khác nhau của đường thẳng như phương trình chính tắc, phương trình tham số, hoặc phương trình tổng quát tùy thuộc vào yêu cầu của bài tập.
– Sử dụng đồ thị hóa: Vẽ đồ thị đường thẳng trên hệ tọa độ ba chiều sẽ giúp bạn hình dung và hiểu rõ hơn về vị trí và hình dạng của đường thẳng trong không gian.
– Áp dụng kiến thức từ hình học không gian: Sử dụng kiến thức về hình học không gian để hiểu rõ hơn về các mối quan hệ giữa các đường thẳng và mặt phẳng trong không gian.
-Thực hành với nhiều dạng bài tập: Làm nhiều bài tập với các dạng khác nhau của phương trình đường thẳng trong không gian để làm quen và nắm vững kiến thức.
– Kiểm tra lại kết quả và giải thích cẩn thận: Sau khi làm xong bài tập, hãy kiểm tra lại kết quả và đảm bảo bạn đã giải thích rõ ràng và logic cho từng bước giải quyết vấn đề.
-Tự học và ôn tập thêm: Nếu gặp khó khăn trong việc hiểu và làm bài tập, hãy tự học thêm từ sách giáo khoa hoặc tài liệu tham khảo. Đồng thời, ôn tập lại các kiến thức cơ bản về đại số và hình học để giúp bạn hiểu sâu hơn về phương trình đường thẳng trong không gian.
Nhớ rằng, việc hiểu và làm bài tập về phương trình đường thẳng trong không gian đòi hỏi sự kiên nhẫn và thực hành thường xuyên. Hãy tự tin và kiên nhẫn trong quá trình học tập!
4. Bài tập trắc nghiệm phương trình đường thẳng trong không gian Lớp 12 Bài 3 chọn lọc hay nhất:
Câu 1: Trong không gian Oxyz, một đường thẳng (d) có:
A. 1 vectơ chỉ phương duy nhất
B. 2 vectơ chỉ phương
C. 3 vectơ chỉ phương
D. Vô số vectơ chỉ phương.
Đáp án: D
Câu 2: Phương trình nào sau đây là phương trình chính tắc của đường thẳng đi qua hai điểm A (1; 2; -3) và B (3; -1; 1) ?
A. 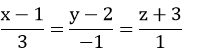
B. 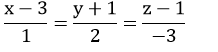
C. 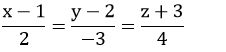
D. 
Đáp án: C
Câu 3: Tọa độ giao điểm M của đường thẳng d và mặt phẳng (α), biết: 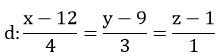 và (α):3x+5y-z-2=0 là:
và (α):3x+5y-z-2=0 là:
A. (1;0;1)
B. (0;0;-2)
C. (1;1;6)
D. (12;9;1)
Đáp án: B
Câu 4: Cho đường thẳng 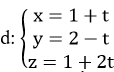 và mặt phẳng (α):x+3y+z+1=0 Trong các mệnh đề sau, tìm mệnh đề đúng:
và mặt phẳng (α):x+3y+z+1=0 Trong các mệnh đề sau, tìm mệnh đề đúng:
A. d //(α)
B. d cắt (α)
C. d ⊂ (α)
D. d⊥(α)
Đáp án: A
Câu 5: Cho đường thẳng và mặt phẳng (α):x+y+z-4=0 Trong các mệnh đề sau, tìm mệnh đề đúng:
A. d cắt (α)
B. d //(α)
C. d ⊂(α)
D. d⊥(α)
Đáp án: C
Câu 6: Hãy tìm kết luận đúng về vị trí tương đối giữa hai đường thẳng:
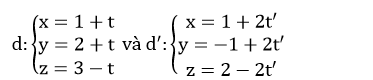
A. d cắt d’
B. d≡d’
C. d chéo với d’
D. d//d’
Đáp án: D
Câu 7: Giao điểm của hai đường thẳng:
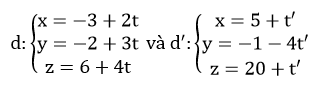 là:
là:
A. (-3;-2;6)
B. (3;7;18)
C. (5;-1;20)
D. (3;-2;1)
Đáp án: B
Câu 8: Tìm m để hai đường thẳng sau đây cắt nhau:
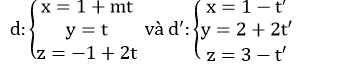
A. m=0
B. m=1
C. m=-1
D. m=2
Đáp án: A
Câu 9: Khoảng cách từ điểm M (-2; -4; 3) đến trục Ox là:
A. 5
B. 2
C. 1
D. 11
Đáp án: A
Câu 10: Gọi H là hình chiếu vuông góc của điểm A (2; -1; -1) đến trục Ox. Độ dài AH là:
A. 5
B. ![]()
C. 2
D. ![]()
Đáp án: D
Câu 11: Khoảng cách từ điểm M (2; 0; 1) đến đường thẳng 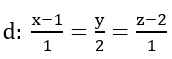 là:
là:
A. ![]()
B. ![]()
C. ![]()
D.
Đáp án: C
Câu 12: Bán kính của mặt cầu tâm I (1; 3; 5) và tiếp xúc với đường thẳng  là:
là:
A. ![]()
B. 14
C. ![]()
D. 7
Đáp án: A
Câu 13: Khoảng cách giữa hai đường thẳng:
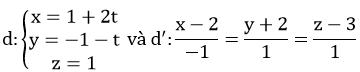 là:
là:
A. ![]()
B. 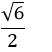
C. 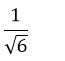
D. ![]()
Đáp án: B
THAM KHẢO THÊM:




