Hệ phương trình đối xứng hai ẩn là dạng bài tập mà các em học sinh thường xuyên gặp phải trong các bài kiểm tra cũng như các kỳ thi toán học. Dưới đây là bài viết về chủ đề: Hướng dẫn giải hệ phương trình đối xứng hai ẩn lớp 9, mời các thầy cô giáo và các em học sinh theo dõi.
Mục lục bài viết
1. Hướng dẫn giải hệ phương trình đối xứng hai ẩn lớp 9 loại 1:
a. Dạng của hệ phương trình
– là một loại hệ phương trình đặc biệt, với đặc điểm là khi hoán đổi giữa hai ẩn x và y trong mỗi phương trình của hệ, thì hệ vẫn giữ nguyên dạng ban đầu. Để hiểu rõ hơn về hệ phương trình đối xứng loại 1 và cách giải, chúng ta có thể xem xét ví dụ sau.
– Ví dụ: Hệ phương trình
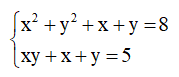
Khi thay x bởi y và thay y bởi x thì được hệ
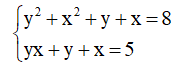
Ta thấy mỗi phương trình của hệ không thay đổi nên hệ đã cho là hệ đối xứng loại 1
b. Cách giải
Bước 1: Biến đổi biểu thức ở hai phương trình của hệ theo tổng và tích của x, y
Bước 2: Đặt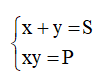 
với điều kiện (S^2 ≥ 4P)
Bước 3: Tìm S, P thỏa mãn điều kiện (S^2 ≥ 4P). Khi đó x, y là nghiệm của phương trình t^2 – Sx + P = 0
Bước 4: Kết luận
Ví dụ: giải hệ phương trình
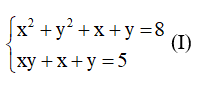
Giải
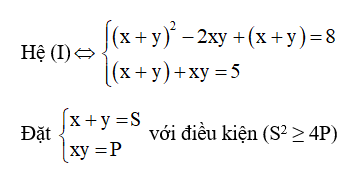
Từ S + P = 5 ⇒ P = 5 – S. Thế vào phương trình S^2 + S -2P = 8 ta được
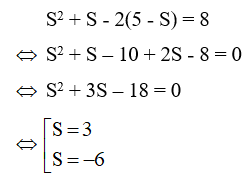
* Với S = 3 ⇒ P = 5 – 3 = 2 thỏa mãn điều kiện (S^2 ≥ 4P)
Ta có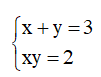 
, theo Vi-et x, y là nghiệm của phương trình:
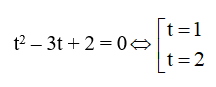
Suy ra hệ có hai nghiệm: x = 1 và y = 2, x =2 và y = 1
* Với S = -6 ⇒ P = 5 – (-6) = 11 không thỏa mãn điều kiện (S^2 ≥ 4P) nên loại
Vậy hệ đã cho có hai nghiệm: x = 1 và y = 2, x =2 và y = 1
2. Hướng dẫn giải hệ phương trình đối xứng hai ẩn lớp 9 loại 2:
a. Dạng của hệ phương trình
– Là hai phương trình hai ẩn x và y, trong đó, mỗi phương trình khi hoán đổi giữa x và y sẽ trở thành phương trình kia và ngược lại, nhưng hệ không thay đổi. Điều này có thể được minh họa bằng ví dụ sau:
– Ví dụ: Hệ phương trình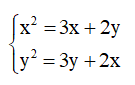 
Khi thay x bởi y và thay y bởi x thì được hệ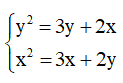 
Ta thấy phương trình này trở thành phương trình kia và ngược lại nhưng hệ không thay đổi nên hệ đã cho là hệ phương trình đối xứng loại 2
b. Cách giải
– Bước 1: Trừ vế với vế của hai phương trình cho nhau ta được phương trình dạng
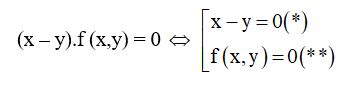
-Bước 2: Kết hợp (*) với 1 phương trình của hệ, kết hợp (**) với 1 phương trình của hệ ta được hai hệ phương trình. Giải hai hệ phương trình đó
-Bước 3: Kết luận
Ví dụ: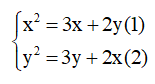 
Giải
Lấy (1) – (2) ta được:
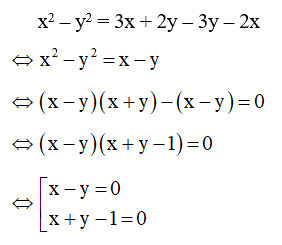
Kết hợp x – y = 0 với phương trình (1) ta có hệ:
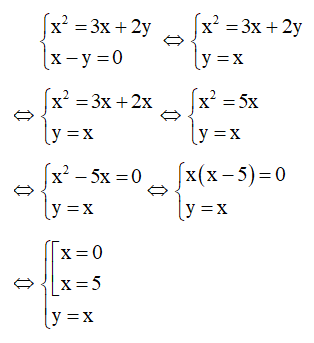
Với x = 0 thì y = x = 0
Với x = 5 thì y = x = 5
Kết hợp x + y – 1 = 0 với phương trình (1) ta có hệ:
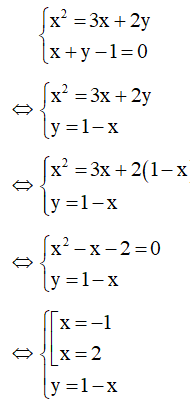
Với x = -1 thì y = 1 – x = 1 + 1 = 2
Với x = 2 thì y = 1 – x = 1 – 2 = -1
Vậy hệ phương trình có 4 nghiệm : (0;0), (5;5), (-1;2), (2;-1)
3. Bài tập có đáp án:
Câu 1: Hệ phương trình sau có bao nhiêu nghiệm: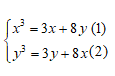 
A. 1
B. 2
C. 3
D. 4
Lời giải:
Hướng dẫn:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
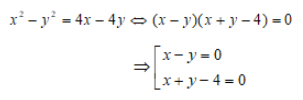
TH1: x = y. Thay x = y vào phương trình (1) ta sẽ có:
x^2 = 3x – x = 0
<=> x^2 – 12x = 0
<=> x (x – 12) = 0
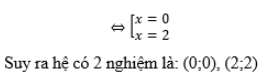
TH2: Ta có phương trình sau:
x + y – 4 = 0. Thay y = 4 – x vào phương trình (1) ta được:
x^2 – 4x + 4 = 0 <=> (x – 2) ^2 = 0 =>x = 2
Với x = 2 ⇒ y = 2. Suy ra hệ có nghiệm là: (2;2)
Vậy hệ phương trình có 2 nghiệm là: (0;0), (2;2).
Chọn đáp án B.
Câu 2: Hệ phương trình sau có bao nhiêu nghiệm: Cách giải hệ phương trình đối xứng loại 2 cực hay | Toán lớp 9
A. 4
B. 2
C. 3
D. 5
Lời giải:
Hướng dẫn:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
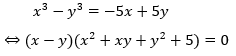
TH1: x – y = 0. Thay x = y vào phương trình (1) ta sẽ có:
x^3 = 3x + 8x = 0
<=> x^3 – 11x = 0
<=> x (x^2 – 11) = 0
TH2: Ta có phương trình như sau:
Chọn đáp án C.
Câu 3: Hệ phương trình dưới đây có bao nhiêu nghiệm: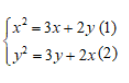 
A. 1
B. 2
C. 3
D. 4
Lời giải:
Hướng dẫn:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
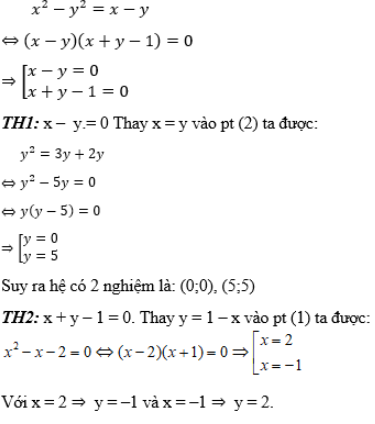
Suy ra hệ có 2 nghiệm (2;-1); (-1;2)
Vậy hệ phương trình có 4 nghiệm là:
(0;0), (5;5), (2;-1), (-1;2).
Chọn đáp án đúng là D.
Câu 4: Hệ phương trình sau có bao nhiêu nghiệm: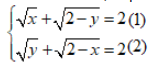 
A. 1
B. 2
C. 3
D. 4
Lời giải:
Hướng dẫn chi tiết:
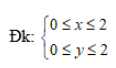
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
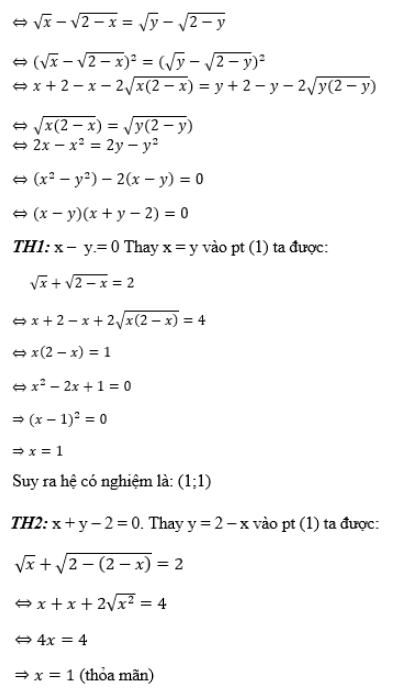
Với x = 1 ⇒ y = 1. Suy ra hệ có nghiệm là: (1; 1),
Vậy hệ phương trình có 1 nghiệm là: (1;1).
Chọn đáp án A.
Câu 5: Hệ phương trình sau có bao nhiêu nghiệm: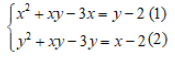 
A. 4
B. 3
C. vô số nghiệm
D. vô nghiệm
Lời giải:
Hướng dẫn chi tiết:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
Vậy hệ phương trình có vô số nghiệm là: (x ∈ R, y = 2 – x).
Chọn đáp án C.
Câu 6: Hệ phương trình sau: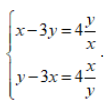 
Khẳng định nào sau đây đúng ?
A. Hệ phương trình có vô số nghiệm.
B. Hệ phương trình có 3 nghiệm.
C. Hệ phương trình có 4 nghiệm.
D. Hệ phương trình có 1 nghiệm.
Lời giải:
Hướng dẫn chi tiết:
Đk: x ≠ 0, y ≠ 0
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
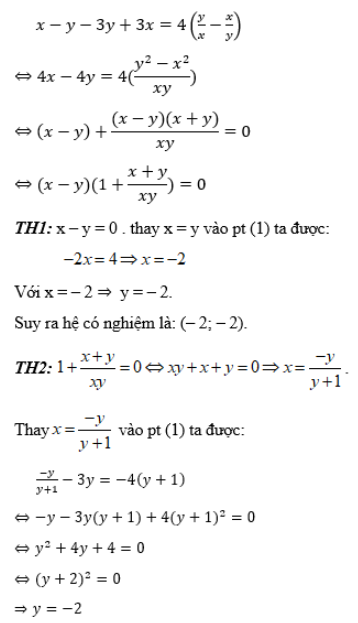
Với y = –2 ⇒ x = –2 ™. Suy ra hệ có nghiệm là: (– 2; – 2).
Vậy hệ phương trình có 1 nghiệm là: (– 2; – 2).
Chọn đáp án D.
Câu 7: Hệ phương trình sau: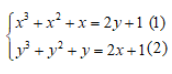 
. Khẳng định nào sau đây đúng ?
A. Hệ phương trình có vô số nghiệm.
B. Hệ phương trình có 2 nghiệm.
C. Hệ phương trình có 4 nghiệm.
D. Hệ phương trình có 3 nghiệm.
Lời giải:
Hướng dẫn:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
x3 – y3 + x^2 – y^2 + x – y = 2y – 2x
⇔ (x – y)(x^2 + xy + y^2 ) + (x – y)(x + y) + 3(x – y) = 0
⇔ (x – y)(x^2 + y^2 + xy + x + y + 3) = 0
TH1: x – y = 0 . thay x = y vào pt (1) ta được:
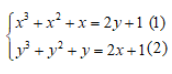
Với x = – 1 ⇒ y = – 1 và x = 1 ⇒ y = 1. Suy ra hệ có 2 nghiệm là: (– 1; – 1), (1;1).
TH2: x^2 + y^2 + xy + x + y + 3 = 0 ⇔ x^2 + (y + 1)x + y^2 + y + 3 = 0 (3)
Ta có: △x = (y + 1)^2 – 4(y^2 + y + 3) = y^2 + 2y + 1 – 4y^2 – 4y – 12 = -(3y^2 + 2y + 11) (*)
Tính: Δy’ = 1 – 33 = -32 < 0. Suy ra pt (*) vô nghiệm.
Suy ra pt (3) vô nghiệm.
Vậy hệ phương trình có 2 nghiệm là: (– 1; – 1), (1;1).
Chọn đáp án B.
Câu 8: Hệ phương trình sau: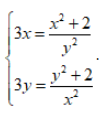 
. Khẳng định nào sau đây đúng?
A. Hệ phương trình vô nghiệm.
B. Hệ phương trình có 2 nghiệm.
C. Hệ phương trình có 1 nghiệm.
D. Hệ phương trình có 3 nghiệm
Lời giải:
Hướng dẫn:
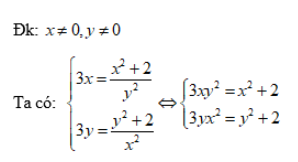
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
Từ hệ phương trình ta thấy, x > 0, y > 0 ⇒ x + y + 3xy > 0. Vậy phương trình (3) vô nghiệm.
Vậy hệ phương trình có 1 nghiệm là: (1; 1).
Chọn đáp án C.
Câu 9: Hệ phương trình sau có bao nhiêu nghiệm: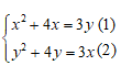 
A. 2
B. 3
C. vô số nghiệm
D. vô nghiệm
Lời giải:
Hướng dẫn:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
Suy ra phương trình vô nghiệm
Vậy hệ phương trình có 4 nghiệm là: (0;0), (-1;-1)
Chọn đáp án A.
Câu 10: Hệ phương trình sau có bao nhiêu nghiệm: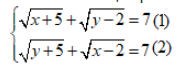 
A. 1
B. 2
C. 3
D. 4
Lời giải:
Hướng dẫn:
Lấy phương trình (1) trừ phương trình (2) ta sẽ có:
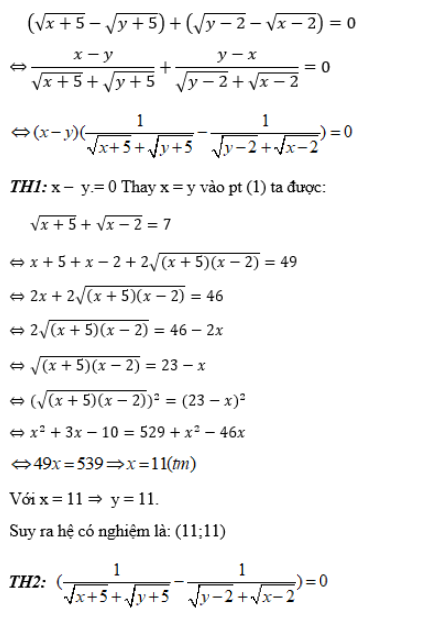
Vì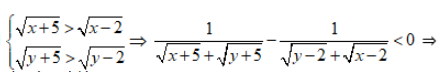 
phương trình vô nghiệm.
Vậy hệ phương trình có 1 nghiệm là: (11;11).
Chọn đáp án A.
THAM KHẢO THÊM:
