Hằng đẳng thức giúp các em học sinh trong quá trình làm bài đặc biệt những bài tập khó một cách vô cùng hiệu quả và hữu ích. Dưới đây là bài viết về chủ đề: 7 hằng đẳng thức đáng nhớ lớp 8 và hệ quả chuẩn nhất, mời bạn đọc theo dõi.
Mục lục bài viết
1. Lý thuyết về 7 hằng đẳng thức đáng nhớ:
Bảy hằng đẳng thức đáng nhớ
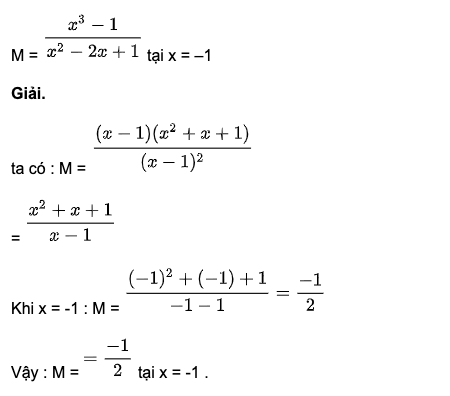
Bình phương của một tổng

Ngoài ra, ta có các hằng đẳng thức hệ quả của 7 hằng đẳng thức trên. Thường sử dụng trong khi biến đổi lượng giác, chứng minh đẳng thức, bất đẳng thức,…
Hệ quả 7 hằng đẳng thức đáng nhớ

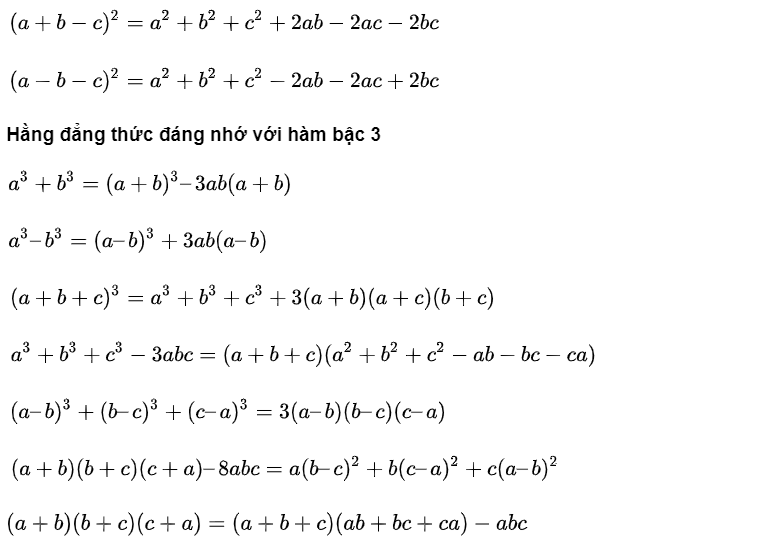
2. Các dạng toán ứng dụng 7 hằng đẳng thức đáng nhớ:
Dạng 1 : Tính giá trị của biểu thức
Bài 1 :tính giá trị của biểu thức : A = x2 – 4x + 4 tại x = -1
Giải.
Ta có : A = x2 – 4x + 4 = A = x2 – 2.x.2 + 22 = (x – 2)2
Tại x = -1 : A = ((-1) – 2)2=(-3)2= 9
Vậy : A(-1) = 9
Dạng 2 : Chứng minh biểu thức A không phụ thuộc vào biến
B = (x – 1)2 + (x + 1)(3 – x)
Giải.
B =(x – 1)2 + (x + 1)(3 – x)
= x2 – 2x + 1 – x2 + 3x + 3 – x
= 4 : hằng số không phụ thuộc vào biến x.
Dạng 3 : Tìm giá trị nhỏ nhất của biểu thức
C = x2 – 2x + 5
Giải.
Ta có : C = x2 – 2x + 5 = (x2 – 2x + 1) + 4 = (x – 1)2 + 4
Mà : (x – 1)2 ≥ 0 với mọi x.
Suy ra : (x – 1)2 + 4 ≥ 4 hay C ≥ 4
Dấu “=” xảy ra khi : x – 1 = 0 hay x = 1
Nên : Cmin= 4 khi x = 1
Dạng 4 : Tìm giá trị lớn nhất của biểu thức
D = 4x – x2
Giải.
Ta có : D = 4x – x2 = 4 – 4 + 4x – x2 = 4 – (4 + x2 – 4x) = 4 – (x – 2)2
Mà : -(x – 2)2 ≤ 0 với mọi x.
Suy ra : 4 – (x – 2)2 ≤ 4 hay D ≤ 4
Dấu “=” xảy ra khi : x – 2 = 0 hay x = 2
Nên : Dmax= 4 khi x = 2.
Dạng 5 :Chứng minh đẳng thức
(a + b)3 – (a – b)3 = 2b(3a2 + b2)
Giải.
VT = (a + b)3 – (a – b)3
= (a3 + 3a2b + 3ab2 + b3) – (a3 – 3a2b + 3ab2 – b3)
= a3 + 3a2b + 3ab2 + b3 – a3 + 3a2b – 3ab2 + b3
= 6a2b + 2b3
= 2b(3a2 + b2) ->đpcm.
Vậy : (a + b)3 – (a – b)3 = 2b(3a2 + b2)
Dạng 6 : Chứng minh bất đẳng thức
Biến đổi bất đẳng thức về dạng biểu thức A ≥ 0 hoặc A ≤ 0. Sau đó dùng các phép biến đổi đưa A về 1 trong 7 hằng đẳng thức.
Dang 7: Phân tích đa thức thành nhân tử
F = x2 – 4x + 4 – y2
Giải.
Ta có : F = x2 – 4x + 4 – y2
= (x2 – 4x + 4) – y2 [nhóm hạng tử]
= (x – 2)2 – y2 [đẳng thức số 2]
= (x – 2 – y )( x – 2 + y) [đẳng thức số 3]
Vậy : F = (x – 2 – y )( x – 2 + y)
Bài 1: A = x3 – 4x2 + 4x
= x(x2 – 4x + 4)
= x(x2 – 2.2x + 22)
= x(x – 2)2
Bài 2: B = x 2 – 2xy – x + 2y
= (x 2– x) + (2y – 2xy)
= x(x – 1) – 2y(x – 1)
= (x – 1)(x – 2y)
Bài 3: C = x2 – 5x + 6
= x2 – 2x – 3x + 6
= x(x – 2) – 3(x – 2)
= (x – 2)(x – 3)
Dạng 8 : Tìm x. biết :
x2 ( x – 3 ) – 4x + 12 = 0
Giải.
x2 ( x – 3 ) – 4x + 12 = 0
x2 ( x – 3 ) – 4(x – 3 ) = 0
( x – 3 ) (x2 – 4) = 0
( x – 3 ) (x – 2)(x + 2) = 0
( x – 3 ) = 0 hay (x – 2) = 0 hay (x + 2) = 0
x = 3 hay x = 2 hay x = –2
vậy : x = 3; x = 2; x = –2
Dạng 9 : Thực hiện phép tính phân thức
Tính giá trị của phân thức

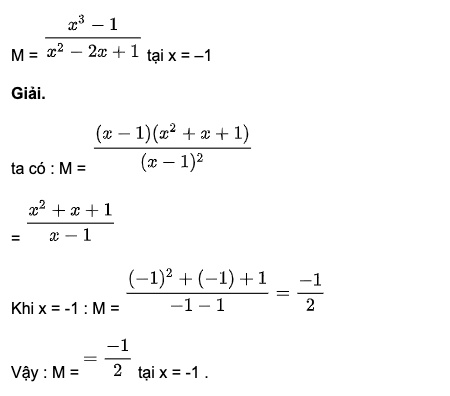
3. Bài toán về 7 hằng đẳng thức đáng nhớ:
Bài 1. Thực hiện phép tính:
a) (2x – 1)3
b) (x + 4)3
c) (x – 2)2
d) (2x + 1)2
e) x3 + 64
f) 8×3 – 27
Lời giải:
a) (2x – 1)3
= (2x)3 – 3.(2x)2.1 + 3.2x.12 – 13
= 8×3 -12×2 + 6x – 1.
b) (x + 4)3
= x3 + 3.x2.4 + 3.x.42 + 43
= x3 + 12×2 + 48x + 64.
c) (x – 2)2
= x2 – 2.x.2 + 22
= x2 – 4x + 4.
d) (2x + 1)2
= (2x)2 + 2.2x.1 + 12
= 4×2 + 4x + 1.
e) x3 + 64
= x3 + 43
= (x + 4)(x2 + 4x + 42)
= (x + 4)(x2 + 4x + 16).
f) 8×3 – 27
= (2x)3 – 33
= (2x – 3)<(2x)2 + 2x.3 + 32>
= (2x – 3)(4×2 + 6x + 9).
Bài 2. Tính giá trị của các biểu thức A, B dưới đây:
a) A = x3 + 6×2 + 12x + 8 tại x = 48
b) B = x3 – 3×2 + 3x – 1 tại x = 101
Lời giải:
a) A = x3 + 6×2 + 12x + 8 tại x = 48
Ta có: A = A = x3 + 6×2 + 12x + 8
= x3 + 3.x2.2 + 3.x.22 + 23
= (x + 2)3
Với x = 48 ta có giá trị của biểu thức A là:
A = (48 + 3)3 = 503 = 125000
b) B = x3 – 3×2 + 3x – 1 tại x = 101
Ta có: B = x3 – 3×2 + 3x – 1
= x3 – 3. x2.1 + 3.x.12 – 13
= (x – 1)3
Với x = 101 ta có giá trị biểu thức B là:
B = (101 – 1)3 = 1003 = 1000000.
Bài 3. Tính nhanh
a) 222
b) 992
c) 1993
d) 1013
e) 19.21
Lời giải:
a) 222
= (20 + 2)2
= 202 + 2.20.2 + 22
= 400 + 80 + 4
= 484.
b) 992
= (100 – 1)2
= 1002 – 2.100.1 + 12
= 10000 – 200 + 1
= 9801.
c) 1993
= (200 -1)3
= 2003 – 3.2002.1 + 3.200.12 – 13
= 8000000 – 120000 + 600 – 1
= 7880599.
d) 1013
= (100 + 1)3
= 1003 + 3.1002.1 + 3.100.12 + 13
= 1000000 + 30000 + 300 + 1
= 1030301.
e) 19.21
= (20 – 1)(20 + 1)
= 202 – 12
= 400 – 1
= 399.
Bài 4. Rút gọn biểu thức:
a) A = (3x – 1)3 – 4x(x – 2) + (2x – 1)2
b) B = (x + 1)3 – 2×2(x – 2) + x3
Lời giải:
a) A = (3x – 1)3 – 4x(x – 2) + (2x – 1)2
= (3x)3 – 3.(3x)2.1 + 3.3x.12 – 13 – 4×2 + 8x + 4×2 – 4x + 1
= 27×3 – 27×2 + 9x -1 + 4x + 1
= 27×3 – 27×2 + 13x
b) B = (x + 1)3 – 2×2(x – 2) + x3
= x3 + 3×2 + 3x + 1 – 2×3 + 4×2 + x3
= 7×2 + 3x + 1.
Bài 5. Cho đa thức 2x² – 5x + 3 . Viết đa thức trên dưới dạng 1 đa thức của biến y trong đó y = x + 1.
Lời Giải
Theo đề bài ta có: y = x + 1 => x = y – 1.
A = 2x² – 5x + 3
= 2(y – 1)² – 5(y – 1) + 3 = 2(y² – 2y + 1) – 5y + 5 + 3 = 2y² – 9y + 10
Bài 6. Tính nhanh kết quả các biểu thức sau:
a) 127² + 146.127 + 73²
b) 98.28– (184 – 1)(184 + 1)
c) 100² – 99² + 98² – 97² + …+ 2² – 1²
d) (20² + 18² + 16² +…+ 4² + 2²) – ( 19² + 17² + 15² +…+ 3² + 1²)
Lời Giải
a) A = 127² + 146.127 + 73²
= 127² + 2.73.127 + 73²
= (127 + 73)²
= 200²
= 40000 .
b) B = 9 8 .2 8 – (18 4 – 1)(18 4 + 1)
= 188 – (188 – 1)
= 1
c) C = 100² – 99² + 98² – 97² + …+ 2² – 1²
= (100 + 99)(100 – 99) + (98 + 97)(98 – 97) +…+ (2 + 1)(2 – 1)
= 100 + 99 + 98 + 97 +…+ 2 + 1
= 5050.
d) D = (20² + 18² + 16² +…+ 4² + 2²) – ( 19² + 17² + 15² +…+ 3² + 1²)
= (20² – 19²) + (18² – 17²) + (16² – 15²)+ …+ (4² – 3²) + (2² – 1²)
= (20 + 19)(20 – 19) + (18 + 17)(18 – 17) + ( 16 +15)(16 – 15)+ …+ (4 + 3)(4 – 3) + (2 + 1)(2 – 1)
= 20 + 19 + 18 + 17 + 16 +15 + …+ 4 + 3 + 2 + 1
= 210
Bài 7. So sánh hai số sau, số nào lớn hơn?
a) A = (2 + 1)(22+ 1)(24+ 1)(28 + 1)(216 + 1) và B = 232
b) A = 1989.1991 và B = 19902
Gợi ý đáp án
a) Ta nhân 2 vế của A với 2 – 1, ta được:
A = (2 – 1)(2 + 1)(22 + 1)(24 + 1)(28 + 1)(216 + 1)
Ta áp dụng đẳng thức ( a- b)(a + b) = a² – b² nhiều lần, ta được:
A = 232 – 1.
=> Vậy A < B.
b) Ta đặt 1990 = x => B = x²
Vậy A = (x – 1)(x + 1) = x² – 1
=> B > A là 1.








