Hình chữ nhật là gì? Tính chất và dấu hiệu nhận biết thế nào?

1. Hình chữ nhật là gì?

Bạn đã từng bắt gặp vật thể nào hình chữ nhật hay chưa? Nếu có rồi thì tại sao bạn lại nghĩ đó là hình chữ nhật? Cùng chúng tôi đưa ra định nghĩa nhé: Hình chữ nhật là một loại tứ giác đặc biệt, trong đó tất cả bốn góc đều là góc vuông. Nói cách khác, hình chữ nhật là một tứ giác mà mọi góc của nó đều có độ lớn bằng 90 độ.

2. Dấu hiệu nhận biết hình chữ nhật: 

Chúng ta bắt gặp hình chữ nhật trong cuộc sống rất nhiều và cũng gặp rất nhiều bài toán liên quan đến hình chữ nhật, vậy để xác định một tứ giác là hình chữ nhật, ta có thể dựa vào các dấu hiệu sau:

• Có ba góc vuông: Nếu một tứ giác có ba góc vuông, thì tứ giác đó là hình chữ nhật. Do tổng các góc trong một tứ giác luôn bằng 360 độ, nên nếu ba góc là góc vuông (90 độ mỗi góc), góc còn lại cũng phải là góc vuông để tổng đạt 360 độ.
• Hình thang cân có một góc vuông: Nếu một hình thang cân có một góc vuông, thì hình thang đó là hình chữ nhật.
• Hình bình hành có một góc vuông: Nếu một hình bình hành có một góc vuông, thì nó là hình chữ nhật. Điều này xuất phát từ việc trong hình bình hành, các góc đối diện luôn bằng nhau, và nếu một góc là góc vuông, tất cả các góc phải là góc vuông.
• Hình bình hành có hai đường chéo bằng nhau: Nếu một hình bình hành có hai đường chéo bằng nhau, thì hình bình hành đó là hình chữ nhật

3. Tính chất của hình chữ nhật: 

Hình chữ nhật có tất cả các tính chất của hình bình hành và hình thang cân. Cụ thể, những tính chất này bao gồm:

• Tính chất của hình bình hành:

+ Các cạnh đối diện của hình chữ nhật là song song và bằng nhau.

+ Các góc đối diện trong hình chữ nhật cũng bằng nhau.

• Tính chất của hình thang cân:

+ Trong một hình chữ nhật, hai đường chéo luôn bằng nhau và chúng cắt nhau tại trung điểm của mỗi đường chéo.

• Đặc điểm của các đường chéo:

+ Hai đường chéo của hình chữ nhật không chỉ bằng nhau mà còn cắt nhau tại điểm trung điểm của mỗi đường chéo.

4. Các công thức tính toán hình chữ nhật:

Các công thức liên quan đến hình chữ nhật sẽ được tổng hợp như sau:

• Công thức để có thể tính chu vi hình chữ nhật

Chu vi hình chữ nhật được tính bằng tổng độ dài các đoạn thẳng bao quanh hình, cũng chính là đoạn thẳng bao quanh diện tích. Chu vi của một hình chữ nhật chính là gấp đôi tổng chiều dài và chiều rộng của nó.

 Công thức để có thể tính chu vi hình chữ nhật

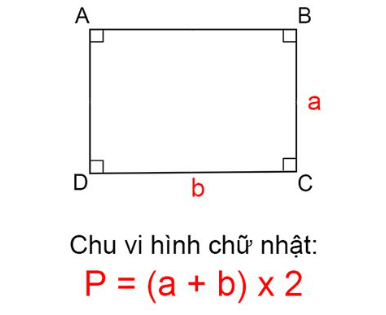
Công thức sẽ là: P=(a+b) x 2

Trong đó:

+ a là chiều dài hình chữ nhật

+ b là chiều rộng của hình chữ nhật cần tính

Ví dụ: Một thửa ruộng hình chữ nhật có chiều dài là 20m cùng với đó là chiều rộng 12m. Hãy tính chu vi của thửa ruộng trên.

Giải:

Chu vi thửa ruộng = (20+12)x2=64m

Vậy chu vi của thửa ruộng trên sẽ là 64m

• Công thức tính diện tích hình chữ nhật

Trường hợp số 1: Tính diện tích hình chữ nhật khi đã nắm được chiều dài và chiều rộng

Diện tích hình chữ nhật sẽ bằng tích của chiều dài nhân với chiều rộng (tính theo cùng đơn vị).

Công thức tính diện tích hình chữ nhật

Công thức: S = a x b

Trong đó:

+ a là chiều dài hình chữ nhật,

+ b là chiều rộng của hình chữ nhật.

+ S là diện tích hình chữ nhật.

Ví dụ: Một thửa ruộng có chiều dài 20m cùng với chiều rộng là 12m. Háy tính diện tích thửa ruộng trên bằng bao nhiêu mét vuông?

Bài giải

Diện tích của thửa ruộng hình chữ nhật trên sẽ được tính như sau:

S = 20 x 12 = 240 (m2)

Vậy thửa ruộng hình chữ nhật trên có diện tích bằng 240 mét vuông

Trường hợp số 2: Tính diện tích hình chữ nhật khi đã biết số đo của một cạnh và đường chéo

Trong trường hợp trên đây cần tính độ dài cạnh còn lại để sau đó tính được diện tích hình chữ nhật theo công thức đã nêu ở trường hợp 1. Giả sử bài toán là ABCD cho hình chữ nhật, biết AB = a.Đường chéo AD là c. Tính diện tích ABCD?

Bước 1: Tính cạnh BD dựa vào định lý Pitago xét tam giác vuông ABD.

Bước 2: Nếu tính cạnh BD, biết AB, ta được dễ dàng tính được diện tích ABCD như trường hợp 1.

Ví dụ:

Cho hình chữ nhật ABCD với chiều dài cạnh AB= 4 cm, đường chéo AC = 5 cm. Tính diện tích hình chữ nhật ABCD ở trên.

Giải

Ta có áp dụng định lý Pitago cho tam giác vuông ABC => cạnh BC có số đo là:

BC^2 =AC^2 – AB^2 => BC^2= 25-16=9 =>BC = 3

Từ đó tính diện tích hình chữ nhật ABCD là

S=AB x BC = 4×3=12 cm2

Bài toán mở rộng

Nếu tăng chiều của một cạnh lên n lần và giữ nguyên cạnh kia thì diện tích bề mặt tăng n lần so với diện tích ban đầu.

Nếu chiều dài tăng n lần và chiều rộng tăng m lần thì thay đổi, diện tích tăng. (n x m) lần diện tích ban đầu

5. Một số dạng bài tập liên quan đến tính chất và dấu hiệu nhận biết của hình chữ nhật: 

Để các bạn hình dung được những kiến thức trên, chúng tôi đã tổng hợp một số dạng bài tập liên quan đến tính chất và dấu hiệu nhận biết của hình chữ nhật: 

Dạng 1: Bài tập liên quan đến dấu hiệu nhận biết hình chữ nhật

Phương pháp giải: Đối với những bài toán ở mức độ nhận biết như thế này, chúng ta chỉ cần quan sát kỹ hình và nắm vững những hiệu về hình chữ nhât. 

Dạng bài 2: Vận dụng tính chất của hình chữ nhật để chứng minh tính chất hình học

Phương pháp giải: Từ những định nghĩa về hình chữ nhật, cạnh, góc, đường chéo của hình chữ nhật và các kiến thức đặc biệt để chứng minh tính chất của hình chữ nhật

Dạng 3: Tìm điều kiện để tứ giác là hình chữ nhật

Phương pháp giải: đây là dạng bài phổ biến rất được ra trong đề thi, chúng ta sẽ vận dụng các kiến thức về định nghĩa, tính chất, dấu hiệu nhận biết để chứng minh.

Sau đây, chúng tôi sẽ giới thiệu đến bạn đọc một số ví dụ minh họa liên quan đến tính chất và dấu hiệu nhận biết của hình chữ nhật. Hy vọng những ví dụ dưới đây sẽ giúp các bạn hiểu thêm những kiến thức về hình chữ nhật và có thể vận dụng chúng vào trong cuộc sống thực tiễn:

Ví dụ 1: Cho hình bình hành ABCD, đường phân giác các góc ^A cắt đường phân giác góc ^B và ^D lần lượt tại G và H, đường phân giác góc ^C cắt đường phân giác góc ^B và ^D lần lượt tại F và E. Chứng minh tứ giác EFGH là hình chữ nhật.

Hướng dẫn:

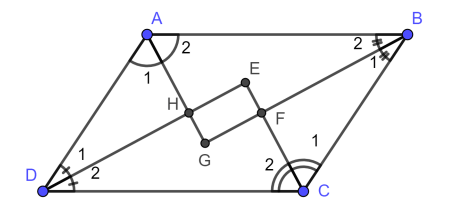
Vì ABCD là hình bình hành nên AB//CD

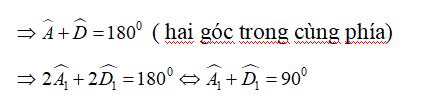
Xét tam giác AHD có:

Chứng minh tương tự ta có:

Suy ra, EFGH là hình chữ nhật.

• Diện tích hình chữ nhật

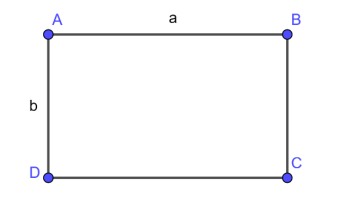
Diện tích hình chữ nhật bằng tích chiều dài nhân với chiều rộng

S = a.b

a, b: là độ dài chiều dài và chiều rộng của hình chữ nhật

Ví dụ 2: Cho hình chữ nhật ABCD có độ dài chiều dài và chiều rộng của hình chữ nhật lần lượt là 7cm và 5cm. Tính diện tích hình chữ nhật?

Hướng dẫn:

Áp dụng công thức ta có, diện tích hình chữ nhật ABCD là:

S = 7.5 =35 (cm2)

Chu vi hình chữ nhật

Chu vi hình chữ nhật bằng hai lần tổng chiều dài và chiều rộng của hình chữ nhật đó.

P = 2( a + b )

a, b: độ dài chiều dài và chiều rộng của hình chữ nhật

Ví dụ 3: Cho hình chữ nhật ABCD có độ dài chiều dài và chiều rộng của hình chữ nhật lần lượt là 7cm và 5cm. Tính chu vi hình chữ nhật?

Hướng dẫn:

Áp dụng công thức ta có, chu vi hình chữ nhật ABCD là:

S = 2( 7 + 5 ) = 24 (cm)