Góc nhọn, góc tù, góc bẹt, góc vuông là những góc cơ bản thường gặp trong hình học nhưng không phải học sinh nào cũng nắm rõ được đặc điểm của những loại góc này nên khi làm bài tập gặp một số khó khăn. Trong nội dung bài viết sau đây Góc nhọn, góc tù, góc bẹt, góc vuông bao nhiêu độ, hãy cùng chúng tôi tìm hiểu rõ hơn về kiến thức cơ bản toán cấp 1 này.
Mục lục bài viết
1. Góc nhọn bao nhiêu độ?
Góc nhọn là góc được tạo nên từ hai đường thẳng có chung một giao điểm trong tam giác bất kỳ hoặc trong mặt phẳng.
Giá trị của góc nhọn thường nhỏ hơn 90⁰. Chúng thường nằm trong khoảng > 0 và < 90⁰.
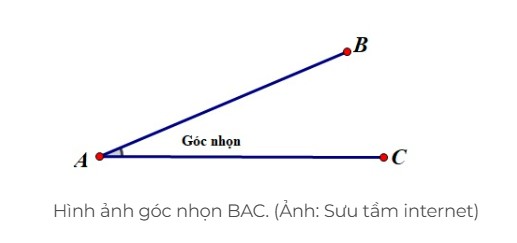
+ Góc nhọn được tạo thành bởi hai đoạn thẳng hay đường thẳng cắt nhau một góc nhỏ hơn 90°.
+ Góc nhọn nhỏ hơn góc vuông.
Cách xác định góc nhọn:
+ Sử dụng thước đo góc: Đặt thước đo góc sao cho một cạnh của góc trùng với vạch 0° trên thước. Đọc giá trị góc tại điểm mà cạnh kia của góc cắt qua thước đo. Nếu giá trị này nhỏ hơn 90° đó là góc nhọn.
+ Áp dụng tính chất của góc nhọn: Góc nhọn luôn có giá trị lớn hơn 0° và nhỏ hơn 90°. Nếu ước lượng rằng góc đó nhỏ hơn góc vuông (90°) thì đó là góc nhọn.
+ Sử dụng eke: Đặt eke sao cho một cạnh của eke trùng với một cạnh của góc. Nếu cạnh còn lại của eke nằm trong khoảng nhỏ hơn 90° thì đó là góc nhọn.
Các dạng toán về góc nhọn:
* Dạng 1: Nhận biết góc nhọn với các góc khác
Phương pháp giải: Dựa vào tính chất định nghĩa của góc nhọn để nhận biết với các góc khác một cách dễ dàng.
Ví dụ: Trong các hình sau, đâu là góc nhọn?
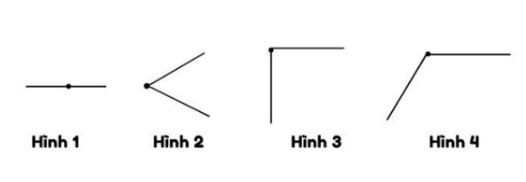
Hướng dẫn trả lời:
Dựa vào tính chất của góc nhọn là góc > 0 và < 90°, ta thấy:
Hình 1: Số đo góc = 0
Hình 2: Số đo góc < 90°
Hình 3: Số đo góc = 90°
Hình 4: Số đo góc > 90°
→ Hình 2 là góc nhọn.
* Dạng 2: Viết tên các góc nhọn trong hình cho trước
Phương pháp giải: Dựa vào tính chất của góc để đọc chính xác tên góc và các cạnh liên quan.
Ví dụ: Viết tên góc nhọn và các cạnh của hình chính xác.
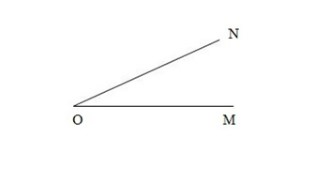
Hướng dẫn trả lời:
Hình trên có góc nhọn đỉnh O, cạnh ON và OM.
* Dạng 3: Vẽ hình tương ứng với góc nhọn
Phương pháp giải: Dựa vào yêu cầu của đề bài, dùng thước đo góc hoặc êke để vẽ góc nhọn tương ứng với số đo góc tương ứng đưa ra.
Ví dụ: Vẽ góc nhọn đỉnh O, cạnh OX, OY với số đo góc tương ứng bằng 70 độ.
Hướng dẫn trả lời:
+ Bước 1: Ta vẽ đường thẳng OX.
+ Bước 2: Dùng thước đo góc đặt ngang bằng đường thẳng OX, điểm 0 độ trên thước sẽ đặt ngay tâm O.
+ Bước 3: Tiến hành xác định điểm 70 độ trên thước tương ứng.
+ Bước 4: Nối đỉnh O tới điểm đã xác định ở bước 3 sẽ được đường thẳng OY.
+ Bước 5: Ta được góc nhọn AOB = 70 độ.
2. Góc tù bao nhiêu độ?
Góc tù là góc được tạo nên bởi hai đoạn thẳng hoặc hai đường thẳng nằm trong cùng mặt phẳng cắt nhau một góc lớn hơn 90⁰.
Giá trị góc tù trong tam giác lớn hơn góc vuông và nhỏ hơn tổng góc trong của hình tam giác là 180⁰.
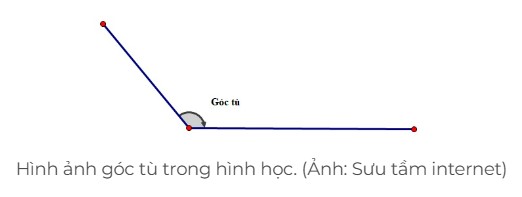
+ Góc từ luôn có giá trị góc nhỏ hơn 180° và lớn hơn góc vuông: 90° < góc tù < 180°.
+ Trong hình học, không có hình học phẳng nào tồn tại góc tù.
Cách xác định góc tù:
+ Sử dụng thước đo góc: Đặt thước đo góc sao cho một cạnh của góc trùng với vạch 0° trên thước. Đọc giá trị góc tại điểm mà cạnh kia của góc cắt qua thước đo. Nếu giá trị này lớn hơn 90° và nhỏ hơn 180°, đó là góc tù.
+ Áp dụng tính chất của góc tù: Góc tù luôn có giá trị lớn hơn 90° và nhỏ hơn 180°. Nếu bạn có thể ước lượng rằng góc đó lớn hơn góc vuông (90°) nhưng nhỏ hơn góc bẹt (180°), thì đó là góc tù.
+ Sử dụng eke: Đặt eke sao cho một cạnh của eke trùng với một cạnh của góc. Nếu cạnh còn lại của eke nằm trong khoảng giữa 90° và 180°, thì đó là góc tù.
Các dạng toán thường gặp về góc tù:
* Dạng 1: Nhận biết góc tù với các góc khác
Phương pháp giải: Dựa vào tính chất định nghĩa của góc tù để nhận biết về các góc khác.
Ví dụ: Trong các hình sau, đâu là góc tù?
Hướng dẫn trả lời:
Dựa vào tính chất của góc tù là góc 90° < góc tù < 180°, ta thấy:
Hình 1: Số đo góc = 0
Hình 2: Số đo góc < 90°
Hình 3: Số đo góc = 90°
Hình 4: Số đo góc > 90°
→ Hình 4 là góc tù.
* Dạng 2: Viết tên các góc tù trong hình cho trước
Phương pháp giải: Dựa vào tính chất của góc để đọc chính xác tên góc và các cạnh liên quan.
Ví dụ: Viết tên góc tù và các cạnh của hình chính xác.
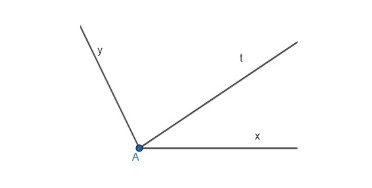
Hướng dẫn trả lời:
Hình trên có góc tù đỉnh A, cạnh Ax và Ay.
* Dạng 3: Vẽ hình tương ứng với góc tù
Phương pháp giải: Dựa vào yêu cầu của đề bài dùng thước đo góc hoặc eke để vẽ góc tù tương ứng với số đo góc tương ứng đưa ra.
Ví dụ: Vẽ góc tù đỉnh O, cạnh Ox, Oy với số đo góc tương ứng bằng 130 độ.
Hướng dẫn trả lời:
+ Bước 1: Ta vẽ đường thẳng Oy.
+ Bước 2: Dùng thước đo góc đặt ngang bằng đường thẳng Oy, điểm 0 độ trên thước sẽ đặt ngay tâm O.
+ Bước 3: Tiến hành xác định điểm 130 độ trên thước tương ứng.
+ Bước 4: Nối đỉnh O tới điểm đã xác định ở bước 3 sẽ được đường thẳng Ox.
+ Bước 5: Ta được góc nhọn yOx = 130 độ.

3. Góc bẹt bao nhiêu độ?
Góc bẹt là góc có giá trị đúng bằng 180⁰.
Những hình cánh quạt khi xòe tròn sẽ tạo thành một góc bẹt hoặc nửa đường tròn cũng có giá trị là góc bẹt.
+ Góc có số đo bằng 180° là góc bẹt.
+ Góc bẹt là góc có hai cạnh là hai tia đối nhau.
+ Góc bẹt nhìn giống như một đường thẳng.
+ Nếu một góc có số đo bằng hai lần góc vuông thì đó chính là góc bẹt.
Cách xác định góc bẹt:
+ Sử dụng thước đo góc: Đặt thước đo góc sao cho một cạnh của góc trùng với vạch 0° trên thước. Đọc giá trị góc tại điểm mà cạnh kia của góc cắt qua thước đo. Nếu giá trị này bằng 180°, đó là góc bẹt.
+.Áp dụng tính chất của góc bẹt: Góc bẹt luôn có giá trị bằng 180°. Nếu ước lượng góc đó tạo thành một đường thẳng, thì đó là góc bẹt.
+.Sử dụng eke: Đặt eke sao cho một cạnh của eke trùng với một cạnh của góc. Nếu cạnh còn lại của eke nằm trên cùng một đường thẳng với cạnh đầu tiên, thì đó là góc bẹt.
Các dạng toán về góc bẹt thường gặp:
* Dạng 1: Nhận biết góc bẹt với các góc khác
Phương pháp giải: Dựa vào đặc điểm, tính chất và khái niệm để xác định được chính xác góc bẹt.
Ví dụ: Cho biết những góc dưới đây góc nào là góc bẹt, Gọi tên góc và xác định đỉnh, các cạnh của góc đó.
Góc xOy = 135°, zAt = 180°, tBk = 90°, xCt = 2. tBk
Hướng dẫn trả lời:
Dựa vào đặc điểm của góc bẹt là góc có số đo bằng 180°. Vậy nên, trong các góc trên thì góc zAt và xCt chính là góc bẹt.
Trong đó:
Góc zAt có đỉnh là A và cạnh là Az, At.
Góc xCt có đỉnh C, cạnh Cx và Ct.
* Dạng 2: Tính số đo góc có phải là góc bẹt không
Phương pháp giải: Dựa vào khái niệm và cách tính số đo góc để có thể giải bài tập chính xác.
Ví dụ: Trên nửa mặt phẳng bờ là tia Ax, vẽ hai tia Ay và Az sao cho góc xAy = 75°, góc yAz = 105°. Hãy tính số đo góc xAz và cho biết góc đó có phải là góc bẹt không?
Hướng dẫn trả lời:
Vì tia Ay và Az cùng nằm trên nửa mặt phẳng bờ là tia Ax và góc xAy = 75°, góc yAz = 105° nên ta có:
Góc xAz = 75° + 105° = 180°
Suy ra: góc xAz = 180°
Vậy góc xAz là góc bẹt.
* Dạng 3: Bài tập tổng hợp
Phương pháp giải: Tùy thuộc vào yêu cầu của mỗi bài tập, các em sẽ đọc và phân tích kỹ đề bài để đưa ra cách giải chính xác nhất.
4. Góc vuông bao nhiêu độ?
Góc vuông là góc được cắt nhau bởi hai đoạn thẳng, đường thẳng tạo thành một góc bằng 90⁰.
Trong đời sống thực tế, những hình ảnh thể hiện góc vuông như kim giờ và kim phút chỉ 12h15p, 3h, 3h30, 6h45,… hay đỉnh của mái nhà với sàn nhà sẽ tạo góc 90⁰.
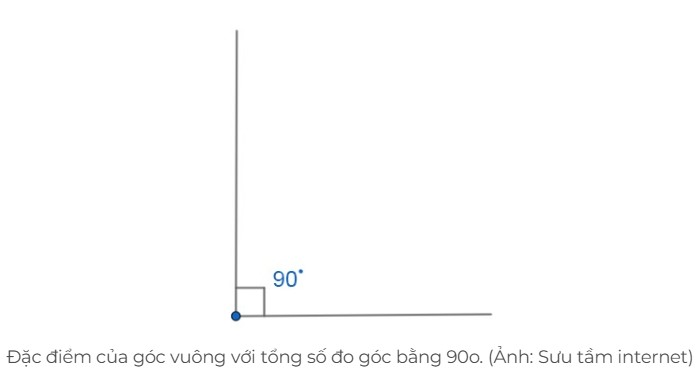
+ Hai cạnh của góc vuông vuông góc với nhau.
+ Số đo của góc vuông là 90 độ.
+ Góc vuông thường được ký hiệu bằng một hình vuông nhỏ tại góc.
Cách xác định góc vuông:
+ Sử dụng thước đo góc: Đặt thước đo góc sao cho một cạnh của góc trùng với vạch 0° trên thước. Đọc giá trị góc tại điểm mà cạnh kia của góc cắt qua thước đo. Nếu giá trị này bằng 90°, đó là góc vuông.
+ Áp dụng tính chất của góc vuông: Góc vuông luôn có giá trị bằng 90°. Nếu bạn có thể ước lượng rằng góc đó tạo thành một góc vuông, thì đó là góc vuông.
+ Sử dụng eke: Đặt eke sao cho một cạnh của eke trùng với một cạnh của góc. Nếu cạnh còn lại của eke nằm vuông góc với cạnh đầu tiên, thì đó là góc vuông.
Các dạng toán thường gặp về góc vuông:
* Dạng 1: Xác định hình đã cho có phải là góc vuông hay không
Phương pháp giải: Dựa vào định nghĩa của góc vuông để giải một cách chính xác. Để chắc chắn có thể dùng thước đo góc hoặc ê ke để tiến hành đo góc có bằng 90 độ hay không.
Ví dụ: Tìm góc vuông và góc không vuông.
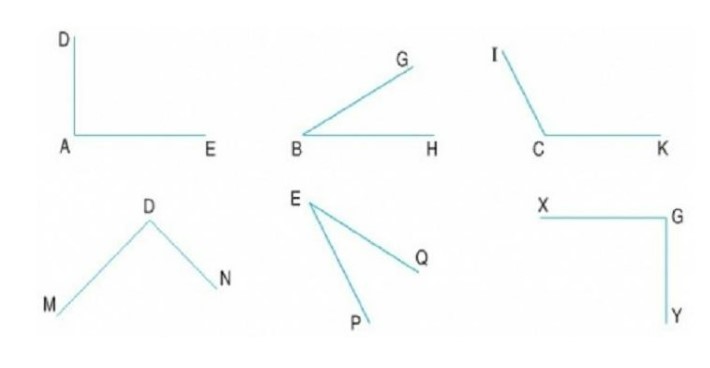
Hướng dẫn trả lời:
Dùng ê – ke đặt vào các góc của hình vẽ ta có:
Những góc vuông là DAE, MDN, XGY; những góc không vuông là GBH, ICK, PEQ.
* Dạng 2: Nêu tên đỉnh hoặc cạnh của góc
Phương pháp giải: Xem lại định nghĩa góc là gì, góc nhọn là gì, góc tù là gì, góc bẹt là gì, góc vuông là gì để có thể nêu tên và các cạnh của góc chính xác.
Ví dụ: Cho hình dưới đây, đọc tên các góc.
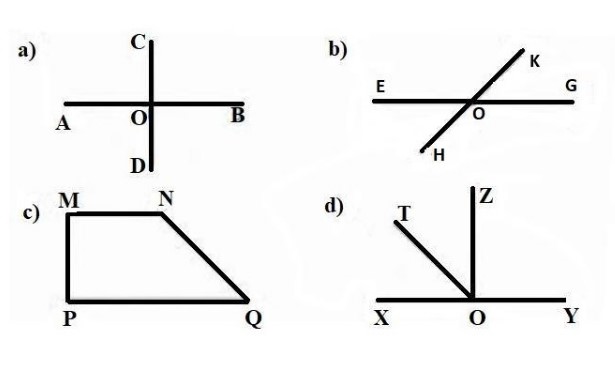
+ Hình a có góc vuông, đỉnh O, các cạnh lần lượt là OA, OB, OC, OD.
+ Hình b là góc không vuông mà là góc nhọn, đỉnh O, các cạnh lần lượt là HE, OH, OK, OG.
+ Hình c là hình thang, với góc vuông ở đỉnh M và P. Ở đỉnh M có cạnh MN và MP; ở đỉnh P có PM và PQ. Còn đỉnh N là góc tù với 2 cạnh tương ứng là NM và NQ. Còn đỉnh Q là góc nhọn với 2 cạnh QN và QP.
+ Hình d có 2 góc vuông đỉnh O, tương ứng với cạnh OX, OZ và OZ, OY. Cùng với 2 góc nhọn đỉnh O là OX và OT, OT và OZ. Cùng 1 góc bẹt là XOY.
* Dạng 3: Đếm số góc vuông trong hình cho trước
Phương pháp giải: Dùng thước eke hoặc thước đo góc để đặt vào từng góc của hình, kiểm tra xem bao nhiêu độ.
Ví dụ: Trên hình có bao nhiêu góc vuông?

Hướng dẫn trả lời:
Xét hình AMNE, có 4 góc vuông với các đỉnh tương ứng là A, M, N, E.
Xét hình MBCDN có 2 góc vuông tại đỉnh M và N.
→ Trong hình ABCDE có tất cả 6 góc vuông.
5. Bài tập vận dụng liên quan kèm đáp án liên quan về góc:
Câu 1: Cho hình vẽ như sau:
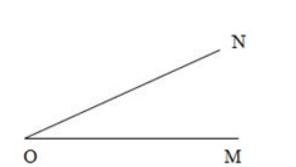
Góc đã cho có đỉnh là:
A. Đỉnh O
B. Đỉnh M
C. Đỉnh N
D. Tất cả các đáp án trên đều đúng.
Đáp án: A.
Quan sát hình trên ta thấy góc đã cho có đỉnh O, cạnh OM và ON.
Câu 2: Cho hình vẽ như sau:

Góc đã cho có cạnh là:
A. Cạnh HDC
B. Cạnh DH, HC
C. Cạnh DH, DC
D. Cạnh DC, HC
Đáp án: B.
Quan sát hình vẽ ta thấy góc đã cho có đỉnh D, cạnh DH, DC.
Câu 3: Trong hình dưới đây, góc đỉnh O cạnh OA và OB là góc nhọn. Đúng hay sai?
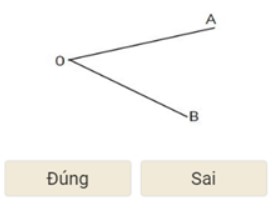
Đáp án: Đúng.
Nhìn hình trên ta thấy góc đỉnh O cạnh OA và OB là góc nhọn.
Vậy khẳng định đã cho là đúng.
Câu 4: Cho hình vẽ như sau:
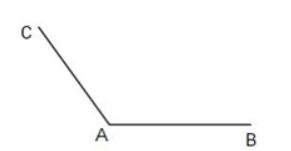
Góc đỉnh A là góc gì?
A. Góc nhọn
B. Góc tù
C. Góc vuông
D. Góc bẹt
Đáp án: B.
Quan sát hình vẽ ta thấy góc đỉnh A cạnh AB, AC là góc tù.
Câu 5: Điền số thích hợp vào ô trống:
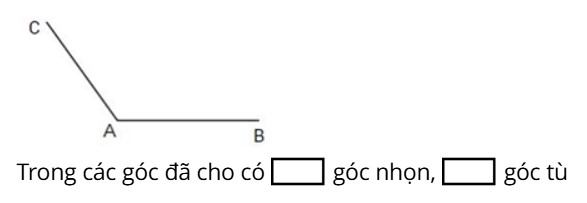
Đáp án: Trong các góc đã cho có 2 góc nhọn, 2 góc tù.
Nhìn hình vẽ ta thấy:
Góc đỉnh A cạnh AB, AC là góc nhọn.
Góc đỉnh O cạnh OP, OQ là góc tù.
Góc đỉnh H cạnh HI, HK là góc vuông.
Góc đỉnh G cạnh GD, GC là góc bẹt.
Góc đỉnh T cạnh TU, TV là góc nhọn.
Góc đỉnh E cạnh EM, EN là góc tù.
Do đó, trong các góc đã cho có 2 góc nhọn, 2 góc tù.
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là 2;2.
Câu 6: Điền số thích hợp vào chỗ trống:
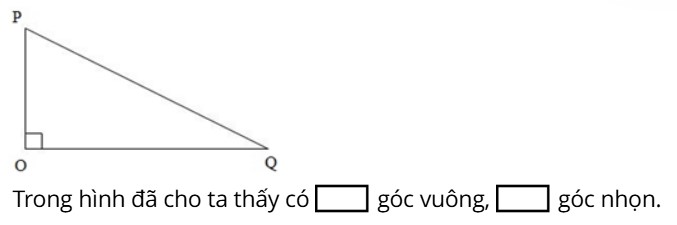
Đáp án: Trong hình đã cho ta thấy có 1 góc vuông, 2 góc nhọn.
Nhìn hình vẽ ta thấy:
Góc đỉnh O cạnh OP, OQ là góc vuông.
Góc đỉnh P cạnh PO, PQ là góc nhọn.
Góc đỉnh Q cạnh QO, QP là góc nhọn.
Vậy trong các góc đã cho có 1 góc vuông, 2 góc nhọn.
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là 1;2.
Câu 7: Cho hình vẽ như bên dưới:
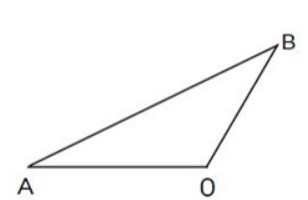
Trong hình vẽ trên có:
A. 1 góc tù, 1 góc nhọn, 1 góc vuông
B. 1 góc vuông, 2 góc nhọn
C. 1 góc vuông, 2 góc tù
D. 1 góc tù, 2 góc nhọn
Đáp án: D.
Nhìn hình trên ta đếm được:
2 góc nhọn:
+ Góc nhọn đỉnh A; cạnh AO, AB.
+ Góc nhọn đỉnh B; cạnh BA, BO.
– 1 góc tù đỉnh O; cạnh OA, OB.
Vậy hình đã cho có 1 góc tù, 2 góc nhọn.
Câu 8: Điền số thích hợp vào ô trống:
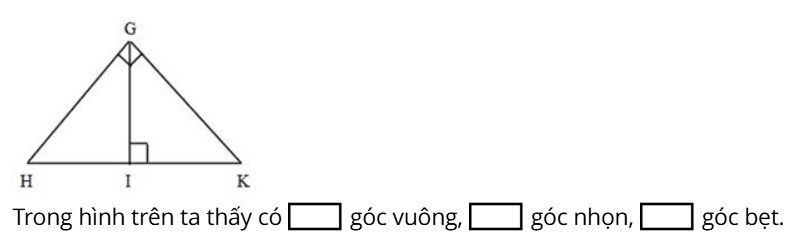
Đáp án: Trong hình trên, ta thấy có 3 góc vuông, 4 góc nhọn, 1 góc bẹt.
Nhìn trong hình trên ta đếm được:
3 góc vuông:
+ Góc vuông đỉnh G; cạnh GH và GK.
+ Góc vuông đỉnh I; cạnh IG và IH.
+ Góc vuông đỉnh I; cạnh IG và IK.
4 góc nhọn:
+ Góc nhọn đỉnh G; cạnh GH và GI.
+ Góc nhọn đỉnh G; cạnh GI và GK.
+ Góc nhọn đỉnh H; cạnh HG và HK.
+ Góc nhọn đỉnh K; cạnh KG và KH.
1 góc bẹt: góc bẹt đỉnh I; cạnh IK và IH.
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là 3;4;1.
Câu 9: Điền số thích hợp vào ô trống:
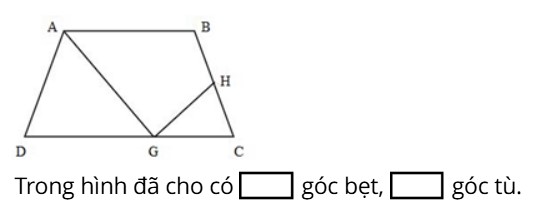
Đáp án: Trong hình đã cho có 2 góc bẹt, 5 góc tù.
Trong hình đã cho có:
5 góc tù:
+ Góc tù đỉnh A; cạnh AD và AB.
+ Góc tù đỉnh B; cạnh BA và BC.
+ Góc tù đỉnh H; cạnh HB và HG.
+ Góc tù đỉnh G; cạnh GD và GH.
+ Góc tù đỉnh G; cạnh GA và GC.
2 góc bẹt:
+ Góc bẹt đỉnh H; cạnh HB và HC.
+ Góc bẹt đỉnh G; cạnh GC và GD.
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là 2;5.
Câu 10: Cho hình vẽ như sau:
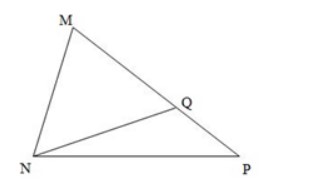
Số góc nhọn có trong hình vẽ trên là:
A. 4
B. 5
C. 6
D. 7
Đáp án: C.
Trong hình đã cho có 6 góc nhọn:
+ Góc nhọn đỉnh M; cạnh MN, MP.
+ Góc nhọn đỉnh N; cạnh NM, NP.
+ Góc nhọn đỉnh N; cạnh NM, NQ.
+ Góc nhọn đỉnh N; cạnh NQ, NP.
+ Góc nhọn đỉnh P; cạnh PN, PM.
+ Góc nhọn đỉnh Q; cạnh QM, QN.
THAM KHẢO THÊM:




