3 điểm thẳng hàng là gì? Lý thuyết Ba điểm thẳng hàng?

1. 3 điểm thẳng hàng là gì?

Ba điểm thẳng hàng là 3 điểm cùng thuộc (hay cùng năm trên) một đường thẳng. Như vậy, khi ba điểm cũng thuộc một đường thẳng, ta nói ba điểm thẳng hàng

Ngược lại, ba điểm không thẳng hàng là khi chúng không cùng thuộc bất kì một đường thẳng nào.

2. Lý thuyết 3 điểm thẳng hàng:

2.1. Quan hệ giữa ba điểm thẳng hàng:

Trong ba điểm thẳng hàng, có một và chỉ một điểm nằm giữa hai điểm còn lại.

Ta cũng có thể nói, nếu có một điểm nằm giữa hai điểm khác thì 3 điểm thẳng hàng.

Giả sử với 3 điểm thẳng hàng A, B, C ta có thể nói:

– Điểm B nằm giữa hai điểm A và C.

– Hai điểm A và B nằm khác phía đối với điểm C.

– Hai điểm B và C nằm cùng phía đối với điểm A.

– Hai điểm A và C nằm khác phía đối với điểm B

2.2. Phương pháp chứng minh 3 điểm thẳng hàng:

Sử dụng tính chất góc bẹt

Chứng minh góc ABC =180 độ => 3 điểm A, B, C thẳng hàng

Sử dụng tiên đề Ơclit

Chứng minh hai đoạn thẳng tạo thành từ ba điểm đã cho, cùng song song với một đường thẳng nào đó.

Ví dụ

Đoạn thẳng AM song song với đường thẳng xy và đoạn thẳng BM song song với đường thẳng xy => 3 điểm A, M, B thẳng hàng

Sử dụng tính chất 2 đường thẳng vuông góc

Chứng minh hai đoạn thẳng, tạo từ 3 điểm đã cho cùng vuông góc với một đường thẳng nào đó.

Chẳng hạn chứng minh : AH vuông góc xy và B vuông góc xy => 3 điểm A, H, B thẳng hàng

Sử dụng tính duy nhất của tia phân giác của một góc khác góc bẹt

Chứng minh: Tia OA và OB cùng là tia phân giác của góc xOy => 3 điểm O, A, B thẳng hàng

Sử dụng tính chất đường trung trực của đoạn thẳng

Chứng minh 3 điểm H, I, K cùng thuộc đường trung trực của AB => 3 điểm H, I, K thẳng hàng

Sử dụng tính chất các đường đồng quy của tam giác

Chứng minh :

+ I là trọng tâm của ΔABC

+ AD là trung tuyến của ΔABC

=> 3 điểm A, I, D thẳng hàng

Sử dụng phương pháp vecto

Để chứng minh ba điểm A, B, C thẳng hàng, ta chứng minh ba điểm đó thỏa mãn đẳng thức (tia AB)=k.(tia AC) với k≠0

3. Bài tập vận dụng:

Bài 1: Cho D ABC vuông tại B. Trên nữa mặt phẳng bờ BC không có điểm A, vẽ tia Cx vuông góc BC. Trên tia Cx lấy M sao cho CM = AB. Chứng minh A, M và D là trung điểm của BC thẳng hàng.

Cách giải: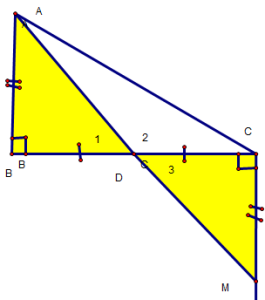

Xét ΔABD và ΔMCD, ta có:

Bˆ=Cˆ

AB = CM (gt)

BD = DC (D là trung điểm cuả BC)

ΔABD=ΔMCD (2 cạnh góc vuông)

⇒D1ˆ=D3ˆ

Mặt khác, D1ˆ+D2ˆ=180∘ (B,C,D thẳng hàng)

⇒D2ˆ+D3ˆ=180∘

hay ADMˆ=180∘

⇒ A,D,M thẳng hàng (góc bẹt)

Bài 2: Cho tam giác ABC có P là trung điểm của AB và hai điểm M,N thỏa mãn các hệ thức →MB–2→MC=→0 và →NA+2→NC=→0. Chứng minh rằng 3 điểm M,N,P thẳng hàng.

Cách giải:

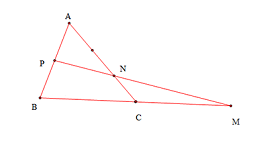
Xét:

→MN=→MC+→NC=→CB+13→CA⇒3→MN=3→CB+→CA     (1)

Xét:

→MP=→MB+→BP=2→CB+12→BA

=2→CB+12(→CA–→CB)=2→CB+12→→CA–12→CB=32→CB+12→CA

⇒2→MP=3→CB+→CA     (2)

Từ (1) và (2) ta có: 3→MN=2→MP⇔→MN=23→MP

Từ đây ta có →MN cùng phương với →MP

Do đó 3 điểm M,N,P thẳng hàng (đpcm)

Bài 3: Cho tứ diện ABCD. Gọi M; N lần lượt là trung điểm của AB và CD. Mặt phẳng (P) qua MN và cắt AD; BC lần lượt tại P và Q. Biết MP cắt NQ tại I. Ba điểm nào sau đây thẳng hàng?

A. I; A; C        B. I; B; D         C. I; A; B        D. I; C; D

Lời giải

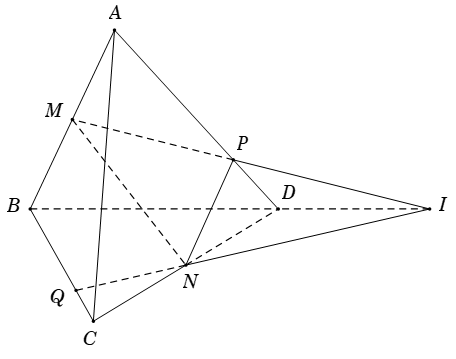
Ta có: (ABD) ∩ (BCD) = BD    (1)

Lại có

Từ (1) và (2) suy ra: I ∈ BD hay 3 điểm I; B; D thẳng hàng

Chọn B

Bài 4: Cho tứ diện SABC. Gọi L; M; N lần lượt là các điểm trên các cạnh SA; SB và AC sao cho LM không song song với AB và LN không song song với SC. Mặt phẳng (LMN) cắt các cạnh AB; BC và SC lần lượt tại K; I; J. Ba điểm nào sau đây thẳng hàng?

A. K; I và J        B. M; I và J        C. N ; I và J        D. M; K và J

Lời giải

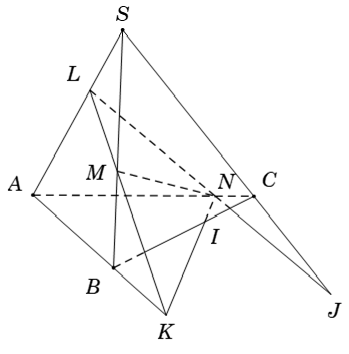
Ta có

– M ∈ SB suy ra M isin; (LMN) ∩ (SBC)    (1)

– I ∈ BC ⊂ (SBC) và I ∈ NK ⊂ (LMN)

⇒ I ∈ (LMN) ∩ (SBC)   (2)

– J ∈ SC ⊂ (SBC) và J ∈ LN ⊂ (LMN)

⇒ J ∈ (LMN) ∩ (SBC)     (3)

Vậy M ; I; J thẳng hàng vì cùng thuộc giao tuyến của mp (LMN) và (SBC)

Chọn B

Bài 5: Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD; M là trung điểm CD; I thuộc đoạn AG; BI cắt mp (ACD) tại J. Chọn mệnh đề sai

A. Giao tuyến của (ACD) và (ABG) là AM

B. 3 điểm A; J; M thẳng hàng.

C. J là trung điểm của AM.

D. Giao tuyến của mp(ACD) và (BDJ) là DJ.

Lời giải

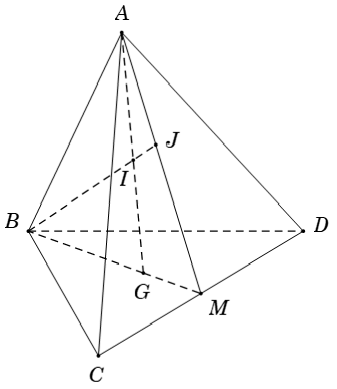
Ta xét các phương án:

   + Ta có: A là điểm chung thứ nhất giữa hai mp (ACD) và mp (GAB)    (1)

Do M là giao điểm của BG và CD nên:

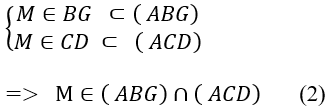
Từ (1) và (2) suy ra: giao tuyến của (ABG) và (ACD) là AM ⇒ A đúng

   + Ta có 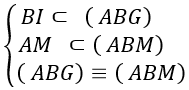 ⇒ AM và BI đồng phẳng

⇒ J = BI ∩ AM nên 3 điểm A; J; M thẳng hàng → B đúng.

   + Ta có

⇒ D đúng

   + Điểm I di động trên AG nên J có thể không phải là trung điểm của AM.

⇒ C sai

Chọn C

Bài 6: Cho tứ diện ABCD. Gọi E; F; G là các điểm lần lượt thuộc các cạnh AB; AC; BD sao cho EF cắt BC tại I; EG cắt AD tại H. Ba đường thẳng nào sau đây đồng quy?

A. CD; EF; EG          B. CD; IG; HF          C. AB; IG; HF          D, AC; IG; BD

Lời giải

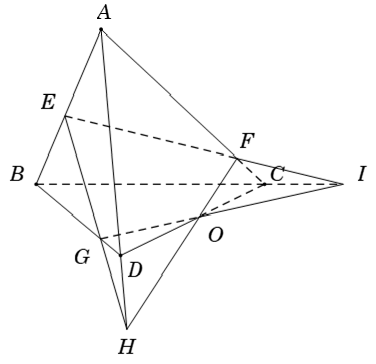
Gọi O là giao điểm của HF và IG . Ta có

– O ∈ HF mà HF ⊂ (ACD) suy ra O ∈ (ACD)

– O ∈ IG mà IG ⊂ (BCD) suy ra O ∈ (BCD)

Do đó O ∈ (ACD) ∩ (BCD)    (1)

Mà (ACD) ∩ (BCD) = CD   (2)

Từ (1) và (2), suy ra O ∈ CD.

Vậy ba đường thẳng CD; IG; HF đồng quy tại O.

Chọn B

Bài 7: Cho hình chóp S.ABCD có đáy ABCD không phải là hình thang. Trên cạnh SC lấy điểm M . Gọi N là giao điểm của SD và mp (AMB). Mệnh đề nào sau đây đúng?

A. Ba đường thẳng AB; CD; MN đôi một song song

B. Ba đường thẳng AB; CD; MN đôi một cắt nhau

C. Ba đường thẳng AB; CD; MN đồng quy

D. Ba đường thẳng AB; CD; MN cùng thuộc một mặt phẳng

Lời giải

– Trong mp (ABCD) gọi I là giao điểm của AD và BC

Trong mp (SBC), gọi K là giao điểm của BM và SI

Trong mp (SAD); gọi N là giao điểm của AK và SD

Khi đó N là giao điểm của đường thẳng SD với mp(AMB)

– Gọi O là giao điểm của AB và CD. Ta có:

   + O ∈ AB mà AB ⊂ (AMB) suy ra O ∈ (AMB)

   + O ∈ CD mà CD ⊂ (SCD) suy ra O ∈ (SCD

⇒ O ∈ (AMB) ∩ (SCD)    (1)

Mà MN = (AMB) ∩ (SCD)    (2)

Từ (1) và (2) , suy ra O ∈ MN.

Vậy ba đường thẳng AB; CD và MN đồng quy.

Chọn C

Bài 8: Cho tứ diện ABCD có G là trọng tâm tam giác BCD, M là trung điểm CD, I là điểm trên đoạn thẳng AG, BI cắt mặt phẳng (ACD) tại J. Khẳng định nào sau đây sai?

A. AM = (ACD) ∩ (ABG)

B. A; J; M thẳng hàng

C. J là trung điểm AM

D. DJ = (ACD) ∩ (BDJ)

Lời giải

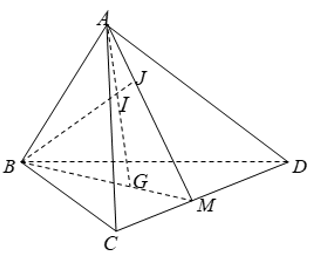
Chọn C

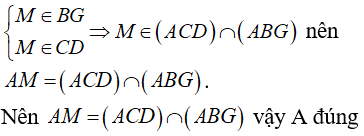
   + Ba điểm A; J và M cùng thuộc hai mặt phẳng phân biệt (ACD) và (ABG) nên A; J; M thẳng hàng, vậy B đúng

   + Vì I là điểm tùy ý trên AG nên J không phải lúc nào cũng là trung điểm của AM.

Bài 9: Cho hình chóp S.ABCD có đáy là hình thang ABCD; AD // BC. Gọi I là giao điểm của AB và CD, M là trung điểm SC. DM cắt mặt phẳng (SAB) tại J. Khẳng định nào sau đây sai?

A. S, I; J thẳng hàng

B. DM ⊂ mp (SCI)

C. JM ⊂ mp(SAB)

D. SI = (SAB) ∩ (SCD)

Lời giải

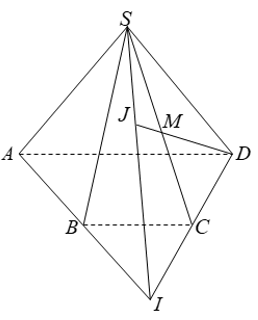
Chọn C

+ Ba điểm S; I và J thẳng hàng vì ba điểm cùng thuộc hai mp

(SAB) và (SCD) nên A đúng

Khi đó: giao tuyến của hai mặt phẳng (SAB) và (SCD) là SI

⇒ D đúng

+ M ∈ SC ⇒ M ∈ (SCI) nên DM ⊂ mp(SCI) vậy B đúng

+ M ∉ (SAB) nên JM ⊄ mp(SAB) vậy C sai

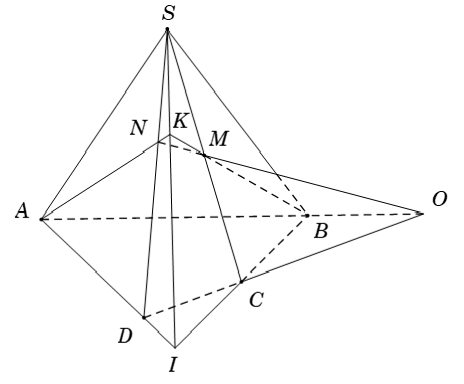
Bài 10: Cho tứ diện SABC có D; E lần lượt là trung điểm của AC; BC và G là trọng tâm của tam giác ABC. Mặt phẳng (α) đi qua AC cắt SE; SB lần lượt tại M, N. Một mặt phẳng (β) đi qua BC cắt SD; SA tương ứng tại P và Q. Gọi I = AM ∩ DN, J = BP ∩ EQ. Khẳng định nào sau đây là đúng?

A. Bốn điểm S, I, J, G thẳng hàng

B. Bốn điểm S, I, J, G không thẳng hàng

C. Ba điểm P, I, J thẳng hàng

D. Bốn điểm I, J, Q thẳng hàng

Lời giải

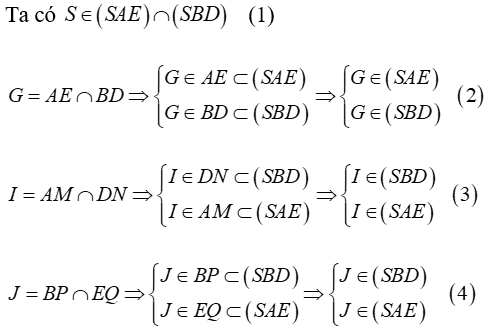
Từ (1), (2), (3) và (4) ta có S; I; J ; G là điểm chung của hai mặt phẳng (SBD) và (SAE) nên chúng thẳng hàng

Chọn A