Bài tập chuyên đề tập hợp, phần tử của tập hợp có đáp án

1. Bài tập chuyên đề tập hợp, phần tử của tập hợp có đáp án mới nhất:

Câu 1: Các viết tập hợp nào sau đây đúng?

A. A = [1; 2; 3; 4]     B. A = (1; 2; 3; 4)

C. A = 1; 2; 3; 4     D. A = {1; 2; 3; 4}

Lời giải:

Các phần tử của tập hợp được viết trong hai dấu ngoặc nhọn { }

Nên cách viết đúng là A = {1; 2; 3; 4}

Chọn đáp án D.

Câu 2: Cho B = {2; 3; 4; 5}. Chọn đáp án sai trong các đáp án sau?

A. 2 ∈ B     B. 5 ∈ B     C. 1 ∉ B     D. 6 ∈ B

Lời giải:

Áp dụng cách sử dụng kí hiệu ∈:

  + 2 ∈ A đọc là 2 thuộc A hoặc là 2 thuộc phần tử của A.

  + 6 ∉ A đọc là 6 không thuộc A hoặc là 6 không là phần tử của A.

Ta thấy 6 không là phần tử của tập hợp B nên 6 ∉ B

Chọn đáp án D.

Câu 3: Viết tập hợp A các số tự nhiên lớn hơn 5 và nhỏ hơn 10.

A. A = {6; 7; 8; 9}     B. A = {5; 6; 7; 8; 9}

C. A = {6; 7; 8; 9; 10}     D. A = {6; 7; 8}

Lời giải:

Viết tập hợp A dưới dạng liệt kê các phân tử

Tập hợp A gồm các phần tử lớn hơn 5 và nhỏ hơn 10 nên A = {6; 7; 8; 9}

Chọn đáp án A.

Câu 4: Viết tập hợp P các chữ cái khác nhau trong cụm từ: “HOC SINH”

A. P = {H; O; C; S; I; N; H}     B. P = {H; O; C; S; I; N}

C. P = {H; C; S; I; N}     D. P = {H; O; C; H; I; N}

Lời giải:

Các chữ cái khác nhau trong cụm từ “HOC SINH” là: H; O; C; S; I; N.

Nên P = {H; O; C; S; I; N}

Chọn đáp án B.

Câu 5: Viết tập hợp A = {16; 17; 18; 19} dưới dạng chỉ ra tính chất đặc trưng

A. A = {x ∈ ℕ|15 < x < 19}     B. A = {x ∈ ℕ|15 < x < 20}

C. A = {x ∈ ℕ|16 < x < 20}     D. A = {x ∈ ℕ|15 < x ≤ 20}

Lời giải:

Nhận thấy các số tự nhiên 16; 17; 18; 19 là các số tự nhiên lớn hơn 15 và nhỏ hơn 20.

Nên A = {x ∈ ℕ|15 < x < 20}

Chọn đáp án B.

2. Bài tập chuyên đề tập hợp, phần tử của tập hợp có đáp án chọn lọc:

Câu 1: Cho tập hợp A = {1; 2; 3; 4} và tập hợp B = {3; 4; 5}. Tập hợp C gồm các phần tử thuộc tập A nhưng không thuộc tập hợp B là?

A. C = {5}     B. C = {1; 2; 5}     C. C = {1; 2}     D. C = {2; 4}

Lời giải:

Các phần tử thuộc tập hợp A mà không thuộc tập hợp B là 1; 2

Nên tập hợp cần tìm là C = {1; 2}

Chọn đáp án C.

Câu 2: Cho tập hợp A = {1; 2; 3; 4} và tập hợp B = {3; 4; 5}. Tập hợp C gồm các phần tử thuộc tập A lẫn tập hợp B là?

A. C = {3; 4; 5}     B. C = {3}     C. C = {4}     D. C = {3; 4}

Lời giải:

Các phần tử thuộc tập hợp A lẫn tập hợp B là 3;4.

Nên tập hợp cần tìm là C = {3; 4}

Chọn đáp án D.

Câu 3: Cho hình vẽ

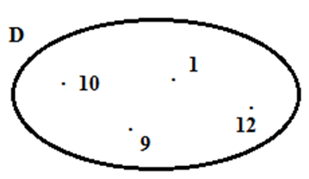
Tập hợp D là?

A. D = {8; 9; 10; 12}     B. D = {1; 9; 10}     C. D = {9; 10; 12}     D. D = {1; 9; 10; 12}

Lời giải:

Dựa vào hình vẽ ta thấy các phần tử của tập hợp D gồm 1; 9; 10; 12

Nên tập hợp D là D = {1; 9; 10; 12}

Câu 4: Tập hợp A = {x ∈ ℕ|22 < x ≤ 27} dưới dạng liệt kê các phần tử là?

A. A = {22; 23; 24; 25; 26}     B. A = {22; 23; 24; 25; 26; 27}

C. A = {23; 24; 25; 26; 27}     D. A = {23; 24; 25; 26}

Lời giải:

Các số tự nhiên lớn hơn 22 và nhỏ hơn hoặc bằng 27 là 23; 24; 25; 26; 27

Nên tập hợp cần tìm là A = {23; 24; 25; 26; 27}

Chọn đáp án C.

Câu 5: Tập hợp P gồm các số tự nhiên lớn hơn 50 và không lớn hơn 57. Kết luận nào sau đây sai?

A. 55 ∈ P     B. 57 ∈ P     C. 50 ∉ P     D. 58 ∈ P

Lời giải:

Tập hợp P gồm các số tự nhiên lớn hơn 50 và không lớn hơn 57 là 51; 52; 53; 54; 55; 56; 57

Nên tập hợp đó là P = {51; 52; 53; 54; 55; 56; 57}

Có 58 ∉ P. Vậy đáp án D sai

Chọn đáp án D.

Câu 6: Cho hình vẽ sau

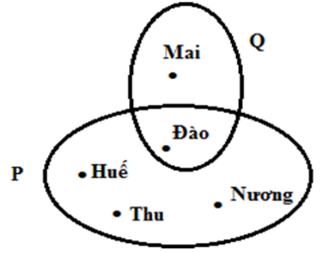
Tập hợp P và tập hợp Q gồm?

A. P = { Huế; Thu; Nương }; Q = { Đào; Mai }

B. P = { Huế; Thu; Nương; Đào}; Q = { Đào; Mai }

C. P = { Huế; Thu; Nương; Đào}; Q = { Mai }

D. P = { Huế; Thu; Đào}; Q = { Đào; Mai }

Lời giải:

Tập hợp P gồm các bạn tên Đào; Huế; Nương; Thu

Tập hợp Q gồm các bạn tên Mai; Đào

Nên ta có: P = { Huế; Thu; Nương; Đào}; Q = { Đào; Mai }

Chọn đáp án B.

Câu 7: Cho hình vẽ sau:

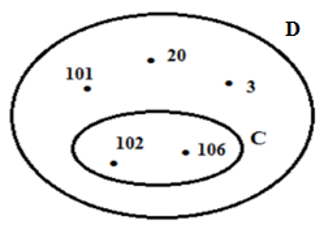
Tập hợp C và tập hợp D gồm?

A. C = {102; 106} và D = {20; 101; 102; 106}

B. C = {102; 106} và D = {3; 20; 102; 106}

C. C = {102; 106} và D = {3; 20; 101}

D. C = {102; 106} và D = {3; 20; 101; 102; 106}

Lời giải:

Ta có: C = {102; 106} và D = {3; 20; 101; 102; 106}

Chọn đáp án D.

3. Ôn tập lý thuyết:

Câu 1: Hãy cho một số ví dụ về tập hợp thường gặp trong thực tế đời sống hàng ngày và một số ví dụ về tập hợp thường gặp trong toán học?

Câu 2: Hãy nêu cách viết một tập hợp, các ký hiệu thường gặp trong tập hợp.

Câu 3: Một tập hợp có thể có bao nhiêu phần tử?

Câu 4: Có gì khác nhau giữa tập hợp N và N*?

Lời giải:

Câu 1:

Dưới đây là một số ví dụ về tập hợp cho bạn tham khảo:

Ví dụ về tập hợp thường gặp trong thực tế:

Tập hợp đồ dùng học tập, bao gồm bút, sách vở, thước kẻ, và các dụng cụ khác cần thiết cho việc học tập.

Tập hợp học sinh lớp 6 của một trường, bao gồm tất cả các học sinh đang học lớp 6 tại trường đó.

Tập hợp các môn học trong một chương trình đào tạo, bao gồm Toán, Ngữ văn, Tiếng Anh, và các môn khác.

Ví dụ về tập hợp trong toán học:

Tập hợp các số tự nhiên, gồm các số từ 1, 2, 3, … và tiếp tục không giới hạn.

Tập hợp các số tự nhiên nhỏ hơn 10, bao gồm các số từ 1 đến 9.

Tập hợp các số chẵn trong khoảng từ 1 đến 20, bao gồm các số 2, 4, 6, …, 20.

Hi vọng các ví dụ trên sẽ giúp bạn hiểu rõ hơn về khái niệm tập hợp trong toán học và trong thực tế.

Câu 2:

Có thể có nhiều cách để mô tả một tập hợp. Dưới đây là hai cách phổ biến:

Cách 1: Liệt kê các phần tử trong tập hợp. Bằng cách này, chúng ta có thể đưa ra danh sách các thành viên của tập hợp, từng phần tử một. Ví dụ, nếu chúng ta có một tập hợp gồm các số tự nhiên từ 1 đến 5, ta có thể viết tập hợp này như sau: {1, 2, 3, 4, 5}.

Cách 2: Chỉ ra tính chất đặc trưng của tập hợp đó. Thay vì liệt kê từng phần tử, chúng ta có thể mô tả tập hợp dựa trên các đặc điểm chung của nó. Ví dụ, nếu chúng ta có tập hợp các số chẵn từ 0 đến 10, ta có thể viết tập hợp này như sau: {x | x là số chẵn từ 0 đến 10}.

Với hai cách tiếp cận khác nhau này, chúng ta có thể mô tả một tập hợp một cách chi tiết và linh hoạt hơn, tùy thuộc vào mục đích và ngữ cảnh sử dụng

+ Các ký hiệu thường gặp trong tập hợp:

Câu 3:

Một tập hợp là một khái niệm trong toán học, và nó có thể có đặc điểm khác nhau. Một tập hợp có thể chứa một phần tử duy nhất, có thể chứa nhiều phần tử đa dạng, hoặc có thể là một tập hợp vô hạn với vô số phần tử. Ngược lại, một tập hợp cũng có thể không chứa bất kỳ phần tử nào. Điều này phụ thuộc vào các quy tắc và định nghĩa được áp dụng trong ngữ cảnh cụ thể.

Câu 4:

+ Tập hợp N là tập hợp số tự nhiên

+ Tập hợp N* là tập hợp số tự nhiên khác 0