Chuyên đề Toán học lớp 7: Tiên đề Ơ-clit về đường thẳng song song được chúng tôi sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.
Mục lục bài viết
1. Lý thuyết tiên đề Ơ-clit về đường thẳng song song:
Tiên đề Ơ-clit nói rằng “Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.” Điều này có nghĩa là nếu bạn chọn một điểm bất kỳ nằm ngoài một đường thẳng, thì bạn chỉ có thể vẽ một đường thẳng duy nhất đi qua điểm đó mà song song với đường thẳng ban đầu. Điều này là một phần quan trọng của định nghĩa về đường thẳng song song trong hình học Euclid và đóng góp vào tính chất cơ bản của đường thẳng trong không gian hai chiều. Nếu có nhiều hơn 1 đường thẳng, đó là trường hợp các đường thẳng trùng nhau.
Tiên đề Ơ-clit về đường thẳng song song là một trong những tiền đề cơ bản trong hình học Euclid, và nó đã được chứng minh và xác minh qua nhiều thế kỷ. Khả năng áp dụng của tiên đề này trong nhiều lĩnh vực toán học và khoa học khác nhau đã giúp xây dựng nền tảng cho nhiều khái niệm quan trọng. Các ứng dụng của tiên đề Ơ-clit bao gồm:
– Hình học Euclid: Tiên đề Ơ-clit là một phần quan trọng của hình học Euclid, hình học phẳng và không gian, và nó hình thành cơ sở cho việc chứng minh nhiều định lý hình học quan trọng.
– Đo lường và hình thức học: Trong hình học, tiên đề Ơ-clit cho phép xây dựng các công cụ đo lường, như goniometer, và thiết kế các hình thức học dựa trên tính chất của các đường thẳng song song và góc.
– Công nghệ và xây dựng: Trong ngành xây dựng và công nghệ, hiểu biết về tiên đề Ơ-clit là quan trọng để thiết kế và xây dựng các công trình như cầu, tòa nhà, và đường sắt. Điều này đảm bảo tính ổn định và an toàn của các công trình này.
– Các ứng dụng trong toán học khác: Tiên đề Ơ-clit không chỉ giới hạn trong hình học mà còn có ảnh hưởng đến nhiều lĩnh vực khác của toán học, bao gồm đại số và lý thuyết đồng tử. Như vậy, tiên đề Ơ-clit không chỉ có giá trị trong hình học, mà còn ứng dụng rộng rãi trong nhiều lĩnh vực khác trong toán học và các ngành công nghiệp khác.
Tính chất đường thẳng song song: Khi hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba, ta có các quy tắc sau đây liên quan đến các góc:
– Hai góc so le còn lại bằng nhau: Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba, thì hai góc so le (góc nằm ở hai bên của đường cắt và trên hai đường song song) sẽ bằng nhau.
– Hai góc đồng vị bằng nhau: Hai góc đồng vị là hai góc nằm ở vị trí tương ứng khi một đường thẳng cắt hai đường thẳng song song và số đo của chúng luôn luôn bằng nhau.
– Hai góc trong cùng phía bù nhau: Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba, thì hai góc trong cùng phái (góc nằm ở hai bên của đường cắt và trên cùng một đường song song) bù nhau, tức là tổng của chúng bằng 180 độ.
2. Bài tập về tiên đề Ơ-clit về đường thẳng song song:
Bài 1: Chọn câu đúng:
A. Qua điểm A ngoài đường thẳng m, có vô số đường thẳng song song với m
B. Qua điểm A ngoài đường thẳng m, có duy nhất một đường thẳng song song với m
C. Qua điểm A nằm ngoài đường thẳng d, có hai đường thẳng phân biệt cùng song song với d
D. Nếu hai đường thẳng AB và AC cùng song song với đường thẳng d thì hai đường thẳng AB và AC song song với nhau.
Bài 2: Trong số các câu sau có bao nhiêu câu đúng:
(I) Hai góc đồng vị bằng nhau;
(II) Hai góc so le ngoài bằng nhau;
(III) Hai góc trong cùng phía bằng nhau;
(IV) Hai góc so le trong bằng nhau.
A. 1 B. 2 C. 3 D. 4
Bài 3. Hai đường thẳng xx’ và yy’ song song với nhau bị cắt bởi một cát tuyến tại 2 điểm A và B. Gọi At là tia phân giác của ∠xAB.
a) Tia At có cắt đường thẳng yy’ hay không? Vì sao?
b) Cho ∠xAB = 80°. Tính ∠ACB = ?
Bài 4. Cho hình vẽ:
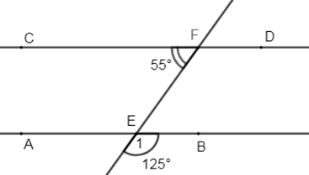
Biết CFE = 55, E1 = 125. Khi đó:
A. AEF = 125
B. AB // CD
C. Cả A, B đều đúng
D. Cả A, B đều sai
Bài 5. Cho hình vẽ dưới đây, biết c. Tính x, y
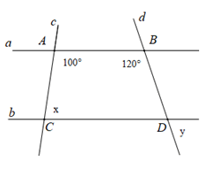
A. x = 80° ; y = 80°
B. x = 60° ; y = 80°
C. x = 80° ; y = 60°
D. x = 60° ; y = 60°
Bài 6. Cho hình vẽ:
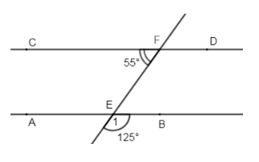
Biết ∠CFE = 55°, ∠E1 = 125°, khi đó:
A. ∠AEF = 125°
B. AB // CD
C. Cả A, B đều đúng
D. Cả A, B đều sai
Bài 7. Điền nội dung phù hợp vào chỗ trống: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng … với đường thẳng kia.”
A. vuông góc;
B. song song;
C. trùng nhau;
D. cắt nhau.
Bài 8. Điền cụm từ thích hợp vào chỗ trống: “Nếu một đường thẳng cắt hai đường thẳng … thì hai góc đồng vị bằng nhau.”
A. song song;
B. vuông góc;
C. giao nhau;
D. trùng nhau.
Bài 9. Qua điểm M nằm ngoài đường thẳng a, ta vẽ ba đường thẳng qua M và song song với a thì:
A. Ba đường thẳng song song;
B. Ba đường thẳng cắt nhau tại A;
C. Ba đường thẳng vuông góc;
D. Ba đường thẳng đó trùng nhau.
3. Hướng dẫn giải tiên đề Ơ-clit về đường thẳng song song:
Bài 1.
Tiền đề Ơ-clit: “Qua một điểm ngoài một đường thẳng, chỉ có một đường thẳng song song với đường thẳng đó.”
Chọn đáp án B.
Bài 2.
Nếu hai đường thẳng song song bị cắt bởi một đường thẳng thứ ba thì:
– Hai góc so le trong còn lại bằng nhau, hai góc so le ngoài bằng nhau.
– Hai góc đồng vị bằng nhau
– Hai góc trong cùng phía bằng nhau Nên cả (I), (II), (III), (IV) đều đúng.
Chọn đáp án D.
Bài 3.
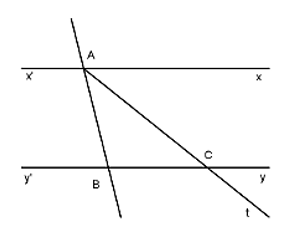
a) Giả sử At không cắt yy’ Suy ra At//yy’ . Theo tiên đề Ơ-clit thì At trùng với xx’ Điều này là vô nghĩa nên At phải cắt yy’ tại C.
b) Ta có:
xAt = 1/2 xAB = 1/2. 80 = 40 (At là tia phân giác xAB)
Mà xAt = ACB (hai góc ở vị trí so le trong và xx’ // yy’).
Vậy ACB = 40
Bài 4.
Phương pháp giải: Áp dụng dấu hiệu nhận biết đường thẳng song song: Nếu đường thẳng c cắt hai đường thẳng a và b, trong các góc tạo thành có 1 cặp góc so le trong bằng nhau thì a // b.
Hướng dẫn giải:
Vì E1 = BEF là hai góc kề bù (gt)
=> E1 + BEF = 180 => BEF = 180 – E1 = 180 – 125 = 55 => BEF = CFE = 55
Mà BEF và CFE là hai góc so le trong nên suy ra AB // CD (dấu hiệu nhận biết hai đường thẳng song song)
Lại có E1 = AEF (hai góc đối đỉnh) nên AEF = 125
Vậy cả A, B đều đúng. Đáp án cần chọn là C.
Bài 5.
Vì a // b nên BAC + ACD = 180 (hai góc trong cùng phía bù nhau)
Suy ra 100 + x = 180 => x = 80
Tương tự ta có: ABD + CDB = 180 => CDB = 60
Suy ra y = CDB = 60 (hai góc đối đỉnh)
Vậy x = 80; y = 60
Chọn đáp án C.
Bài 6.
Vì E1 và BEF là hai góc kề bù (gt) => E1 + BEF = 180 => BEF = 180 – E1 = 180 – 125 = 55 => BEF = CFE = 55
Mà ∠BEF và ∠CFE là hai góc so le trong nên suy ra AB // CD (dấu hiệu nhận biết hai đường thẳng song song)
Lại có ∠E1 = ∠AEF (hai góc đối đỉnh) nên ∠AEF = 125°
Vậy cả A, B đều đúng. Chọn đáp án C.
Bài 7.
Đáp án đúng là: A
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
Bài 8.
Đáp án đúng là: A
Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau.
Bài 9.
Đáp án đúng là: D
Theo tiên đề Euclid ta có: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó Do đó, qua điểm M nằm ngoài đường thẳng a, ta vẽ ba đường thẳng qua M và song song với a thì ba đường thẳng đó phải trùng nhau.
Vậy chọn đáp án D.