Định nghĩa, tính chất, dấu hiệu nhận biết các hình học phẳng được chúng tôi tổng hợp và đăng tải. Tài liệu giúp các em nắm được định nghĩa, tính chất, dấu hiệu nhận biết hình thang cân, hình bình hành, hình thoi, hình vuông, từ đó áp dụng tốt vào giải các bài tập. Dưới đây là nội dung chi tiết các em tham khảo nhé.
Mục lục bài viết
- 1 1. Định nghĩa, tính chất, dấu hiệu nhận biết hình thang cân:
- 2 2. Định nghĩa, tính chất, dấu hiệu nhận biết hình bình hành:
- 3 3. Định nghĩa, tính chất, dấu hiệu nhận biết Hình chữ nhật:
- 4 4. Định nghĩa, tính chất, dấu hiệu nhận biết hình thoi:
- 5 5. Định nghĩa, tính chất, dấu hiệu nhận biết hình vuông:
- 6 6. Định nghĩa, tính chất, dấu hiệu nhận biết Hình tam giác:
1. Định nghĩa, tính chất, dấu hiệu nhận biết hình thang cân:
Định nghĩa:
– Hình thang cân là hình thang có hai góc kề 1 đáy bằng nhau
Tính chất:
– Hình thang cân có:
+ hai góc kề bằng nhau
+ hai đường chéo bằng nhau
Dấu hiệu nhận biết:
– Hình thang có:
+ hai góc kề bằng nhau là hình thang cân
+ hai đường chéo bằng nhau là hình thang cân
Bài tập minh họa
Bài tập 1: Chứng minh hình thang cân:
Ví dụ 1: Hình thang ABCD (AB // CD) có góc ACD = góc BDC. Chứng minh rằng ABCD là hình thang cân.
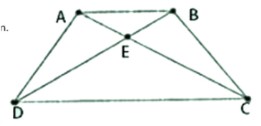
Gọi E là giao điểm của AC và BD.
Do góc ACD = góc BCD nên tam giác ECD có góc C1 = góc D1, nên là tam giác cân. Từ đó suy ra EC = ED. (1)
Tương tự do góc ACD = góc BCD và AB // CD nên tam giác EAB cân tại E, suy ra EA = EB. (2)
Từ (1) và (2) suy ra: EA + EC = EB + ED => AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên hình thang ABCD là hình thang cân (điều phải chứng minh).
Ví dụ 2: Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. CHứng mình EA = EB, EC = ED.
Lời giải:
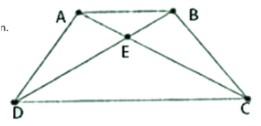
Do ABCD là hình thang cân (giả thiết) nên AD = BC, AC = BD (tính chất hình thang cân)
Xét tam giác ADC và tam giác BCD có:
AD = BC (chứng minh trên)
AC = BD (chứng mình trên)
DC chung
=> Tam giác ADC = tam giác BCD (cạnh – cạnh – cạnh)
Suy ra góc ACD = góc BDC (2 góc tương ứng)
Do đó tam giác EDC cân tại E (dấu hiệu nhận biết tam giác cân) => EC = ED (tính chất tam giac cân)
Lại có: AC = BD (chứng minh trên), EC = ED (chứng minh trên)
=> AC – CE = BD – ED => EA = EB
Vậy EA = EB và EC = ED (điều phải chứng minh).
2. Định nghĩa, tính chất, dấu hiệu nhận biết hình bình hành:
Định nghĩa:
– Là tứ giác có các cạnh đối song song
Tính chất:
– Hình bình hành có:
+ Các cạnh đối bằng nhau
+ Các góc đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
Dấu hiệu nhận biết:
– Tứ giác có:
+ Các cạnh đối song song là hình bình hành
+ Các cạnh đối bằng nhau là hình bình hành
+ Hai cạnh đối song song và bằng nhau là hình bình hành
+ Các góc đối bằng nhau là hình bình hành
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành
3. Định nghĩa, tính chất, dấu hiệu nhận biết Hình chữ nhật:
Định nghĩa:
– Là tứ giác có 4 góc vuông
Tính chất:
– Hình chữ nhật có:
+ Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường
+ tất cả các tính chất của hình thang cân và hình thoi.
Dấu hiệu nhận biết:
– Tứ giác có 3 góc vuông là hình chữ nhật
– Hình thang cân có 1 góc vuông là hình chữ nhật
– Hình bình hành có 1 góc vuông là hình chữ nhật
– Hình bình hành có 2 đường chéo bằng nhau là hình chữ nhật
4. Định nghĩa, tính chất, dấu hiệu nhận biết hình thoi:
Định nghĩa:
Hình thoi là tứ giác có 4 cạnh bằng nha
Tính chất:
– Trong hình thoi có:
+ Hai đường chéo vuông góc với nhau
+ Hai đường chéo là các đường phân giác của các góc của hình thoi và cắt nhau tại trung điểm của mỗi đường
+ Tất cả các tính chất của hình bình hành
Dấu hiệu nhận biết:
– Tứ giác có 4 cạnh bằng nhau là hình thoi
– Hình bình hành có hai cạnh kề bằng nhau là hình thoi
– Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi
– Hình bình hành có 1 đường chéo là đường phân giác của một góc là hình thoi
Bài tập minh họa
Ví dụ 1:
Cho hình thoi ABCD, độ dài mỗi cạnh là 13cm. Gọi O là giao điểm của hai đường chéo. Vẽ OH vuông góc AD. Biết OH = 6cm, tính tỉ số của hai đường chéo BD và AC.
Giải
* Tìm cách giải
Vẽ thêm BK vuông góc với AD để dùng định lí đường trung bình của tam giác, định lí Py-ta-go tính bình phương độ dài của mỗi đường chéo.
* Trình bày lời giải
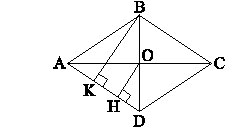
Vẽ BK vuông góc AD.
Xét DBKD có OH // BK (vì cùng vuông góc với AD) và OB = OD nên KH = HD.
Vậy OH là đường trung bình của DBKD.
Suy ra do đó BK = 12cm.
Xét DABK vuông tại K có AK2 = AB2 – BK2 = 132 – 122 = 25 ⇒ AK = 5cm do đó KD = 8cm.
Xét DBKD vuông tại K có BD2 = BK2 + KD2 = 122 + 82 = 208.
Xét DAOH vuông tại H có OA2 = OH2 + AH2 = 62 + 92 = 117.
Ví dụ 2:
Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Đường thẳng AH cắt EF tại D, cắt BC tại G. Gọi M và N lần lượt là hình chiếu của G trên AB và AC. Chứng minh rằng tứ giác DNGM là hình thoi.
*Tìm cách giải
Dùng định lí đường trung bình của tam giác ta chứng minh được tứ giác DNGM là hình bình hành. Sau đó chứng minh hai cạnh kề bằng nhau.
*Trình bày lời giải
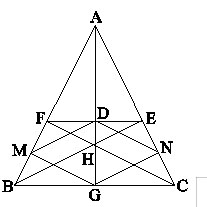
DABE = DACF (cạnh huyền, góc nhọn)
⇒ AE = AF và BE = CF.
Vì H là trực tâm của DABC nên AH là đường cao, đồng thời là đường trung tuyến, từ đó GB = GC và DE = DF.
Vì H là trực tâm của DABC nên AH là đường cao, đồng thời là đường trung tuyến, từ đó GB = GC và DE = DF.
Xét DEBC có GN // BE (cùng vuông góc với AC) và GB = GC nên NE = NC.
Chứng minh tương tự ta được MF = MB.
Dùng định lí đường trung bình của tam giác ta chứng minh được DM // GN và DM = GN nên tứ giác DNGM là hình bình hành.
Mặt khác, DM = DN (cùng bằng của hai cạnh bằng nhau) nên DNGM là hình thoi.
5. Định nghĩa, tính chất, dấu hiệu nhận biết hình vuông:
Định nghĩa:
Hình vuông là tứ giác có 4 góc vuông và 4 cạnh bằng nhau.
Tính chất:
– Hình vuông có các tính chất của hình chữ nhật và hình thoi.
Dấu hiệu nhận biết:
– Hình chữ nhật có hai cạnh kể bằng nhau là hình vuông
– Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông
– Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông
– Hình thoi có một góc vuông là hình vuông
Hình thoi có hai đường chéo bằng nhau là hình vuông.
6. Định nghĩa, tính chất, dấu hiệu nhận biết Hình tam giác:
Tam giác là một hình học có ba đỉnh, ba cạnh và ba góc. Dưới đây là một số đặc điểm và tính chất của hình tam giác:
Tính chất cơ bản: Tam giác có ba đỉnh, ba cạnh và ba góc. Tổng độ dài của ba cạnh của tam giác phải luôn lớn hơn 0.
Dấu hiệu nhận biết: Tổng độ dài hai cạnh bất kỳ của tam giác phải lớn hơn chiều dài cạnh còn lại. Điều này được gọi là nguyên tắc tam giác. Nếu tổng độ dài hai cạnh bất kỳ bằng hoặc nhỏ hơn chiều dài cạnh còn lại, thì không thể tạo thành một tam giác. Tổng độ lớn của hai góc bất kỳ trong tam giác phải lớn hơn 180 độ. Nếu tổng độ lớn của hai góc này bằng 180 độ, thì tam giác đó là một tam giác phẳng.
Phân loại tam giác dựa trên độ dài các cạnh:
Tam giác đều: Các cạnh và góc của tam giác đều có cùng độ dài và góc bằng 60 độ.
Tam giác vuông: Có một góc vuông, tức là một góc bằng 90 độ. Độ dài hai cạnh gần góc vuông được gọi là cạnh góc vuông
Tam giác cân: Hai cạnh đối diện với hai góc bằng nhau có cùng độ dài. Nếu các góc đối diện không bằng nhau, tam giác cân cũng có thể là tam giác vuông cân.
Tam giác nhọn: Tất cả các góc trong tam giác đều nhọn (ít hơn 90 độ).
Tam giác tù: Có ít nhất một góc tù (lớn hơn 90 độ).
Phân loại tam giác dựa trên độ đối xứng:
Tam giác đều có độ đối xứng cao.
Tam giác cân có ít nhất một độ đối xứng.