Lý thuyết Toán lớp 7 có đáp án: Đa thức một biến, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kì thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mục lục bài viết
1. Lý thuyết Đa thức một biến Toán lớp 7 đầy đủ và chi tiết:
* Đa thức một biến
Đa thức một biến thường được biểu diễn dưới dạng tổng của các đơn thức, mỗi đơn thức chứa cùng một biến. Ví dụ, là một đa thức một biến vì nó là tổng của các đơn thức chứa biến , đó là , và .
Một số cụ thể cũng có thể coi là một đa thức một biến. Ví dụ, 7 có thể xem như là đa thức một biến bậc , vì không chứa bất kỳ biến nào.
Bậc của một đa thức một biến là số mũ lớn nhất của biến trong đa thức đó.
Ví dụ 1: Đa thức 5×5 + 4×3 – 2×2 + x là đa thức một biến (biến x); bậc của đa thức là 5.
Ví dụ 2: Cho đa thức sau: 5×7 – 7×6 + 5×5 – 4×4 + 7×6 – 3×2 + 1 – 5×7 – 3×5
Bậc của đa thức đã cho là bao nhiêu?
Hướng dẫn giải:
Thu gọn đa thức ta được:

Đa thức đã cho có bậc là 5.
* Sắp xếp một đa thức một biến
Để thuận lợi cho việc tính toán đối với các đa thức một biến, người ta thường sắp xếp các hạng tử của chúng theo lũy thừa tăng hoặc giảm của biến.
Ví dụ 1: Đối với đa thức P(x) = 6x + 3 – 6×2 + x3 + 2×4
+ Khi sắp xếp các hạng tử của nó theo lũy thừa giảm của biến, ta được:
P(x) = 2×4 + x3 – 6×2 + 6x + 3
+ Khi sắp xếp các hạng tử của nó theo lũy thừa tăng của biến, ta được:
P(x) = 3 + 6x – 6×2 + x3 + 2×4
Nhận xét:
Mọi đa thức bậc 2 của biến x, sau khi đã sắp xếp các hạng tử của chúng theo lũy thừa giảm của biến, đều có dạng: ax2 + bx + c
Trong đó a,b,c là các số cho trước và a ≠ 0.
Chú ý:
+ Để sắp xếp các hạng tử của một đa thức, trước hết ta phải thu gọn đa thức đó.
+ Những chữ đại diện cho các số xác định cho trước được gọi là hằng số.
Ví dụ 2: Cho đa thức P(x) = 2 + 5×2 – 3×3 + 4x – 2x – x3 + 6×5. Thu gọn và sắp xếp đa thức
P(x) = 2 + 5×2 – 3×3 + 4×2 – 2x – x3 + 6×5 = 6×5 + (-3×3 – x3) + (5×2 + 4×2) – 2x + 2 = 6×5 – 4×3 + 9×2 – 2x + 2
* Hệ số
Hệ số của lũy thừa bậc 0 của biến gọi là hệ số tự do; hệ số của lũy thừa cao nhất của biến gọi là hệ số cao nhất.
Ví dụ: Các hệ số của đa thức 6×5 – x4 + 5×2 – x + 2 là 6; -1; 5; -1; 2
Hệ số tự do là: 2
Hệ số cao nhất là: 6
2. Bài tập kèm lời giải:
Bài 1: Thu gọn các đa thức sau và sắp xếp theo lũy thừa giảm dần của biến
a) 2×3 – x5 + 3×4 + x2 – (1/2)x3 + 3×5 – 2×2 – x4 + 1
b) x7 – 3×4 + 2×3 – x2 – x4 – x + x7 – x3 + 5
Lời giải:
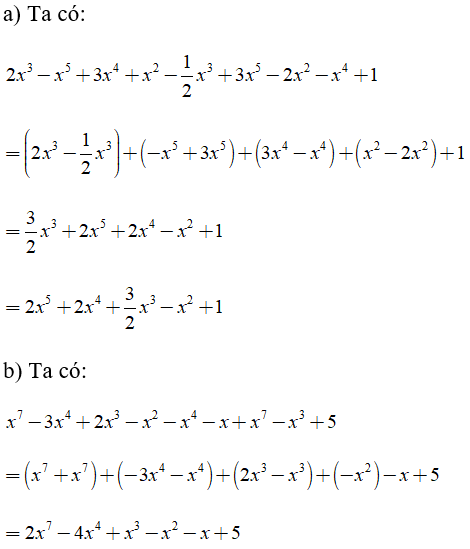
Bài 2: Tính giá trị của các biểu thức sau:
a) x + x2 + x3 + x4 + …. + x99 + x100 tại x = -1
b) x2 + x4 + x6 + …. + x98 + x100 tại x = -1
Lời giải:
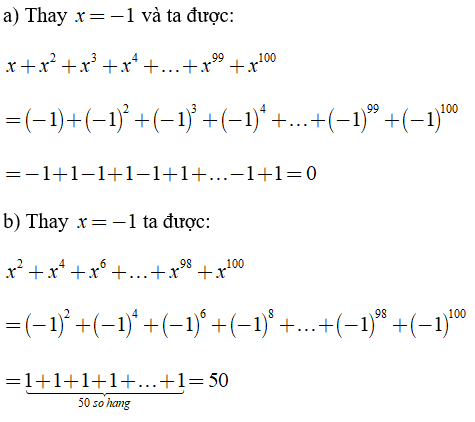
3. Bài tập về cộng trừ đa thức một biến có đáp án:
Bài 1: Tìm hai đa thức P(x) và Q(x) sao cho P(x) + Q(x) = x2 + 1
A. P(x) = x2; Q(x) = x + 1
B. P(x) = x2 + x; Q(x) = x + 1
C. P(x) = x2; Q(x) = -x + 1
D. P(x) = x2 – x; Q(x) = x + 1
Lời giải:
Ta có với P(x) = x2 – x; Q(x) = x + 1
P(x) + Q(x) = x2 – x + x + 1 = x2 + 1
Chọn đáp án D
Bài 2: Cho f(x) = x5 – 3×4 + x2 – 5 và g(x) = 2×4 + 7×3 – x2 + 6. Tìm hiệu f(x) – g(x) rồi sắp xếp kết quả theo lũy thừa tăng dần của biến ta được:
A. 11 + 2×2 + 7×3 – 5×4 + x5
B. -11 + 2×2 – 7×3 – 5×4 + x5
C. x5 – 5×4 – 7×3 + 2×2 – 11
D. x5 – 5×4 – 7×3 + 2×2 + 11
Lời giải:
Ta có

Sắp xếp theo lũy thừa tăng dần của biến ta được
-11 + 2×2 – 7×3 – 5×4 + x5
Chọn đáp án B
Bài 3: Cho p(x) = 5×4 + 4×3 – 3×2 + 2x – 1 và q(x) = -x4 + 2×3 – 3×2 + 4x – 5
Tính p(x) + q(x) rồi tìm bậc của đa thức thu được
A. p(x) + q(x) = 6×3 – 6×2 + 6x – 6 có bậc là 6
B p(x) + q(x) = 4×4 + 6×3 – 6×2 + 6x + 6 có bậc là 4
C. p(x) + q(x) = 4×4 + 6×3 – 6×2 + 6x – 6 có bậc là 4
D. P(x) + q(x) = 4×4 + 6×3 + 6x – 6 có bậc là 4
Lời giải:
Ta có p(x) + q(x)

Bậc của đa thức p(x) + q(x) = 4×4 + 6×3 – 6×2 + 6x – 6 là 4
Chọn đáp án C
Bài 4: Tìm đa thức h(x) biết f(x) – h(x) = g(x) biết
f(x) = x2 + x + 1; g(x) = 4 – 2×3 + x4 + 7×5
A. h(x) = -7×5 – x4 + 2×3 + x2 + x – 3
B. h(x) = 7×5 – x4 + 2×3 + x2 + x + 3
C. h(x) = -7×5 – x4 + 2×3 + x2 + x + 3
D. h(x) = 7×5 + x4 + 2×3 + x2 + x + 3
Lời giải:
Ta có f(x) – h(x) = g(x) ⇒ h(x) = f(x) – g(x)
Mà f(x) = x2 + x + 1; g(x) = 4 – 2×3 + x4 + 7×5 nên h(x) = x2 + x + 1 – (4 – 2×3 + x4 + 7×5)
= x2 + x + 1 – 4 + 2×3 – x4 – 7×5
= -7×5 – x4 + 2×3 + x2 + x – 3
Vậy h(x) = -7×5 – x4 + 2×3 + x2 + x – 3
Chọn đáp án A
Bài 5: Tìm hệ số cao nhất của đa thức k(x) biết f(x) + k(x) = g(x) và f(x) = x4 – 4×2 + 6×3 + 2x – 1; g(x) = x + 3
A. -1 B. 1 C. 4 D. 6
Lời giải:
Ta có f(x) + k(x) = g(x) ⇒ k(x) = g(x) – f(x)
= x + 3 – (x4 – 4×2 + 6×3 + 2x – 1)
= x + 3 – x4 + 4×2 – 6×3 – 2x + 1 = -x4 – 6×3 + 4×2 – x + 4
Nhận thấy số hạng có lũy thừa cao nhất của biến là -x4 nên hệ số cao nhất là -1
Chọn đáp án A
Bài 6: Tìm hệ số tự do của hiệu f(x) – 2.g(x) với
f(x) = 5×4 + 4×3 – 3×2 + 2x – 1; g(x) = -x4 + 2×3 – 3×2 + 4x + 5
A. 7 B. 11 C. -11 D. 4
Lời giải:
– Ta có:

Hệ số cần tìm là -11
Chọn đáp án C
Bài 7: Cho biết M(x) + (x3 + 5×2 – 7x + 1) = 3×4 + x3 – 7 . Câu nào sau đây đúng:
A. M(x) = 3×4 + x3 – 7
B. Bậc của M(x) là 4
C. Hệ số cao nhất của M(x) là 7
D. A, B đúng và C sai
Lời giải:

Bậc của đa thức M(x) là 4
Hệ số cao nhất của M(x) là 3
Suy ra đáp án A, C, D sai, B đúng
Chọn đáp án B
Bài 8: Cho hai đa thức A(x) = 4×2 + 5x + 3 và B(x) = – 4×2 + 5×7 – 5x + 3 . Tìm bậc của đa thức C(x) với C(x) = A(x) + B(x)
A. 2
B. 3
C. 5
D. 7
Lời giải:
Ta có:

Vậy bậc của đa thức C(x) là 7.
Chọn đáp án D
Bài 9: Cho hai đa thức M(y) = 5y3 + y – 6 và N(y) = 5y2 + y – 6 . Tìm đa thức K(y) = M(y) – N(y)

Lời giải:
Ta có:

Chọn đáp án A
Bài 10: Thu gọn đa thức (5×3 + 4×2 – 1) – (4×3 – 4×2 + 1) ta được
A. 0
B. x3 + 8×2 – 2
C. -x3 + 8×2 – 2
D. -x3 – 8×2 – 2
Lời giải:
Ta có:

Chọn đáp án B
4. Bài tập Nghiệm của đa thức một biến chọn lọc, có đáp án:
Bài 1: Cho đa thức f(x) = 2×2 + 12x + 10. Trong các số sau, số nào là nghiệm của đa thức đã cho:
A. -9 B. 1 C. -1 D. -4
Lời giải:
f(-9) = 2.(-9)2 + 12.(-9) + 10 = 64 ≠ 0 ⇒ x = -9 không là nghiệm của f(x)
f(1) = 2.(1)2 + 12.(1) + 10 = 24 ≠ 0 ⇒ x = 1 không là nghiệm của f(x)
f(-1) = 2.(-1)2 + 12.(-1) + 10 = 0 ⇒ x = 1 là nghiệm của f(x)
f(-4) = 2.(-4)2 + 12.(-4) + 10 = -6 ≠ 0 ⇒ x = -4 không là nghiệm của f(x)
Chọn đáp án C
Bài 2: Cho các giá trị của x là 0; -1; 1; 2; -2. Giá trị nào của x là nghiệm của đa thức P(x) = x2 + x – 2
A. x = 1; x = -2
B. x = 0; x = -1; x = -2
C. x = 1; x = 2
D. x = 1; x = -2; x = 2
Lời giải:
P(0) = 02 + 0 – 2 = -2 ≠ 0 ⇒ x = 0 không phải là nghiệm của P(x)
P(-1) = (-1)2 + 1.(-1) – 2 = -2 ≠ 0 ⇒ x = -1 không là nghiệm của P(x)
P(1) = 12 + 1.1 – 2 = 0 ⇒ x = 1 là nghiệm của P(x)
P(2) = 22 + 1.2 – 2 = 4 ≠ 0 ⇒ x = 2 không là nghiệm của P(x)
P(-2) = (-2)2 + 1.(-2) – 2 = 0 ⇒ x = -2 không là nghiệm của P(x)
vậy x = 1; x = -2 là nghiệm của P(x)
Chọn đáp án A
Bài 3: Tập nghiệm của đa thức f(x) = (x + 14)(x – 4) là:
A. {4; 14} B. {-4; 14} C. {-4; -14} D. {4; -14}
Lời giải:

Vậy tập nghiệm của đa thức f(x) là {4; -14}
Chọn đáp án D
Bài 4: Cho đa thức sau f(x) = x2 + 5x – 6. Các nghiệm của đa thức đã cho là:
A. 2 và 3 B. 1 và – 6 C. -3 và -6 D. -3 và 8
Lời giải:

Vậy nghiệm của đa thức f(x) là 1 và -6
Chọn đáp án B
Bài 5: Tổng các nghiệm của đa thức x2 – 16 là:
A. -16 B. 8 C. 4 D. 0
Lời giải:

Vậy x = 4; x = -4 là nghiệm của đa thức x2 – 16
Tổng các nghiệm là 4 + (-4) = 0
Chọn đáp án D




