Cách giải Tìm hai số khi biết tổng và tỉ số của hai số đó lớp 4 gồm các dạng bài tập có phương pháp giải chi tiết và các bài tập điển hình từ cơ bản đến nâng cao giúp học sinh biết cách làm Tìm hai số khi biết tổng và tỉ số của hai số đó lớp 4.
Mục lục bài viết
1. Các bài toán về tìm hai số khi biết tổng và tỉ số của chúng:
Bài 1: Tổng của hai số bằng số lớn nhất của số có hai chữ số. Tỉ số của hai số đó là 4/5. Tìm hai số đó.
Đáp án
Gợi ý: Số lớn nhất có hai chữ số là bao nhiêu ? (99)
Số lớn nhất có hai chữ số là 99. Vậy tổng số của hai số là 99.
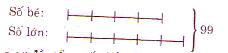
Tổng số phần bằng nhau là.
4 + 5 = 9 (phần)
Số bé là :
99 : 9 × 4 = 44
Số lớn là :
99 – 44 = 55
Đáp số: 55 và 44.
Bài 2: Một hình chữ nhật có chu vi là 350m, chiều rộng bằng 3/4 chiều dài. Tìm chiều dài, chiều rộng của hình chữ nhật đó?
Đáp án
Nửa chu vi là: 350 : 2 = 175(cm)
Ta có sơ đồ:
Chiều dài : |———–|———–|———-|———-|
Chiều rộng: |————|———–|———-|
Tổng số phần bằng nhau là: 3 + 4 = 7(phần)
Chiều dài là: 175 : 7 nhân 4 = 100(m)
Chiều rộng là: 175 – 100 = 75 (m)
Đáp số: chiều dài: 100m
chiều rộng: 75m
Bài 3. Một sợi dây dài 28m được cắt thành hai đoạn, đoạn thứ nhất dài gấp 3 lần đoạn dây thứ hai. Hỏi mỗi đoạn dài bao nhiêu mét?
Đáp án
Ta có sơ đồ:
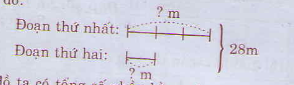
Theo sơ đồ ta có tổng số phần bằng nhau :
3 + 1 = 4 (phần)
Đoạn thứ hai dài:
28 : 4 = 7 (m)
Đoạn thứ nhất dài:
28 – 7 =21 (m)
Bài 4. Tổng của hai số là 72. Tìm hai số đó, biết rằng nếu số lớn giảm 5 lần thì được số bé.
Đáp án
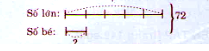
Vì số lớn giảm 5 lần thì được số bé nên số lớn gấp 5 lần số bé.
Tổng số phần bằng nhau là:
5 + 1 = 6 (phần)
Số bé là:
72 : 6 = 12
Số lớn là:
72 – 12 = 60
Đáp số: Số lớn : 60; Số bé : 12.
Bài 5: Tổng của hai số là 96. Tỉ số của hai số đó là 3/5. Tìm hai số đó?
Đáp án
Tổng số phần bằng nhau là:3 + 5 = 8 (phần)
Số bé là: 96 : 8 x 3 = 36
Số lớn là: 96 – 36 = 6
Đáp số : Số bé: 36
Số lớn: 60
Bài 6: Minh và Khôi có 25 quyển vở. Số vở của Minh bằng 2/3 số vở của Khôi. Hỏi mỗi bạn có bao nhiêu quyển vở.
Đáp án
Tổng số phần bằng nhau là: 2 + 3 = 5 (phần)
Số vở của Minh là: 25 : 5 x 2 = 10 (quyển vở)
Số vở của Khôi là : 25 : 5 x 3 = 15 (quyển vở)
Đáp số: Minh: 10 quyển vở
Khôi: 15 quyển vở
Bài 7: Hai kho chứa 125 tấn thóc. Số thóc ở kho thứ nhất bằng 3/2 số thóc ở kho thứ 2. Hỏi mỗi kho chứa bao nhiêu tấn thóc?
Đáp án
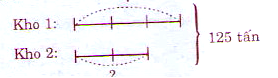
Ta có sơ đồ :3 + 2 = 5( phần)
Kho thứ nhất chứa:
125 : 5 × 3 = 75(tấn)
Kho thứ hai chứa :
125 – 75 = 50 (tấn)
Đáp số: 75 tấn thóc và 50 tấn thóc.
Nói thêm: Ta còn nói số thóc ở kho thứ nhất gấp rưỡi số thóc ở kho thứ hai”.
Bài 8: Một miếng vườn hình chữ nhật, có chu vi 200 m, chiều dài gấp 3 lần chiều rộng. Tính diện tích miếng vườn?
Đáp án
Nửa chu vi mảnh vườn hình chữ nhật là :
200 : 2 = 100 (m)
Ta có sơ đồ:
Chiều rộng: l——l
Chiều dài: l——l——l——l
Theo sơ đồ, tổng số phần bằng nhau là:
3 + 1 = 4 (phần)
Chiều rộng mảnh vườn hình chữ nhật là:
100 : 4 x 1 = 25 (m)
Chiều dài mảnh vườn hình chữ nhật là:
100 – 25 = 75 (m)
Diện tích mảnh vườn hình chữ nhật là:
75 x 25 = 1875 (m2)
Đáp số: 1875 m2
Bài 9: Miếng đất hình chữ nhật có chu vi 240m, chiều rộng bằng 2/3 chiều dài. Tính diện tích hình chữ nhật đó.
Đáp án
Tổng chiều dài và chiều rộng của hình chữ nhật đó là:
240 : 2=120 (m)
Chiều dài hình chữ nhật đó là:
120 : (2 + 3) x 3 = 72 (m)
Chiều rộng hình chữ nhật đó là:
120 : (2 + 3) x 2 = 48 (m)
Diện tích hình chữ nhật đó là:
72 x 48 = 3456 (m2)
Bài 10: Đội tuyển bóng đá mi ni của huyện A tham dự hội khỏe Phù Đổng cấp tỉnh gồm các bạn học sinh lớp 4 và lớp 5. Dự định số bạn tham gia đội tuyển bóng đá đang học lớp 4 chiếm 1/5 của cả đội. Nhưng do một bạn đang học lớp 4 không tham gia được mà thay bởi một bạn đang học lớp 5, khi đó số bạn đang học lớp 4 tham gia chỉ bằng 1/10 số thành viên của cả đội. Tính tổng số thành viên của cả đôi bóng đá mi ni?
Đáp án
Dự định số bạn nữ tham gia đội tuyển bằng 1/4 số nam nên số bạn nữ bằng 1/5 số bạn trong đội tuyển. Sau đó thay một bạn nữ bằng một bạn nam, khi đó số bạn nữ bằng 1/5 số bạn nam nên số bạn nữ bằng 1/6 số bạn của đội tuyển.
Một bạn chiếm số phần học sinh cả đội là:
(số học sinh cả đội tuyển)
Vậy số học sinh đội tuyển của trường A tham gia Hội khoẻ Phù Đổng là:
(học sinh)
Đáp số: 30 học sinh
Bài 11: Đội tuyển của trường A tham gia Hội khoẻ Phù Đổng cấp huyện gồm các bạn học sinh nam và học sinh nữ. Dự định số bạn nữ tham gia đội tuyển chiếm 1/4 số nam nhưng do điều kiện thay bởi một bạn nữ bằng một bạn nam. Khi đó số bạn nữ chiếm 1/5 số nam. Tính xem đội tuyển của trường A đi dự hội thao bao nhiêu học sinh?
Đáp án
Tổng số phần của học sinh lúc ban đầu là :
1 + 4 = 5 ( phần )
Tổng số phần học sinh lúc sau là :
1 + 5 = 6 ( phần )
Lúc ban đầu số học sinh nam so với ban đầu ở trong đội tuyển là :
1 : 5 = ( tổng số học sinh )
Sau khi thay đổi thì số học sinh nam so với số học sinh ở trong đội tuyển là :
1 : 6 = (tổng số học sinh)
Sau khi thay 1 học sinh nữ bằng 1 học sinh nam thì số học sinh nam trong đội tuyển là :
(tổng số học sinh)
Đội tuyển đó có số học sinh là :
= 30 (học sinh)
Đáp số : 30 học sinh trong đội tuyển.
Bài 12: Hình chữ nhật có chu vi là 200m. Chiều dài bằng 3/2 chiều rộng. Tính diện tích của hình chữ nhật?
Lời giải:
Sơ đồ số phần bằng nhau:
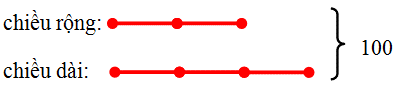
Tổng chiều dài và chiều rộng:
200 : 2 = 100 (m)
Tổng số phần bằng nhau:
3 + 2 = 5 (phần)
Giá trị một phần:
100 : 5 = 20 (m)
Chiều dài của hình chữ nhật:
20 × 3 = 60 (m)
Chiều rộng của hình chữ nhật:
20 × 3 = 40 (m)
Diện tích của hình chữ nhật:
60 × 40 = 2400 (m2)
Đáp số: 2400 (m2).
Bài 13: Tìm hai số biết trung bình cộng của hai số đó bằng 16 và số lớn bằng 5/3 số bé.
Lời giải:
Tổng của hai số đó là:
16 × 2 = 32
Tổng số phần bằng nhau là:
5 + 3 = 8
Số bé là:
32 : 8 × 3 = 12
Số lớn là:
32 – 12 = 20
Đáp số: Số bé: 12; số lớn: 20
2. Cách giải chung bài toán về tìm hai số khi biết tổng và tỉ số:
Cách giải bài toán tìm hai số khi biết tổng và tỉ số là một trong những kỹ năng quan trọng trong toán học. Dưới đây là các bước cơ bản:
Bước 1: Vẽ sơ đồ dựa trên dữ kiện của bài toán. Điều này giúp chúng ta có cái nhìn tổng quan về vấn đề và dễ dàng tìm ra cách tiếp cận.
Bước 2: Xác định tổng số phần bằng nhau. Điều này giúp chúng ta biết cách chia số tổng thành các phần nhỏ như thế nào.
Bước 3: Tìm số bé và số lớn. Có thể chọn tìm số nào trước cũng như ngược lại. Công thức để tính các số này rất đơn giản và tiện lợi.
Số bé = (Tổng : số phần bằng nhau) x số phần của số bé (Hoặc Tổng – số lớn)
Số lớn = (Tổng: số phần bằng nhau) x số phần của số lớn (Hoặc tổng – số bé)
Bước 4: Kết luận và đưa ra đáp số. Đây là bước quan trọng cuối cùng để hoàn thành giải pháp.
Học sinh cũng có thể thực hiện bước thử lại để kiểm chứng kết quả và đảm bảo tính chính xác của câu trả lời.
3. Trường hợp đặc biệt Các bài toán về tìm hai số khi biết tổng và tỉ số:
Khi chúng ta có đề bài không có đầy đủ thông tin về tổng và tỉ số ban đầu. Có một số trường hợp như sau:
Khi chỉ biết tỉ số, nhưng không biết tổng.
Khi chỉ biết tổng, nhưng không biết tỉ số.
Khi cần bổ sung hoặc giảm đi một số để tạo ra tổng (hoặc tỉ) mới và từ đó tìm ra số ban đầu.
Những bài toán như vậy đòi hỏi chúng ta phải thực hiện một bước chuyển đổi để quy về bài toán cơ bản. Đây là một trong những bước quan trọng trong quá trình giải toán học, và sẽ đòi hỏi sự linh hoạt và sáng tạo từ phía người giải.




