Tia phân giác là gì? Lý thuyết Tia phân giác của một góc?

1. Tia phân giác là gì? 

Tia phân giác là một đường thẳng đi qua một góc của một hình học và chia góc đó thành hai góc bằng nhau. Tia phân giác có thể được vẽ cho các góc trong hay ngoài hình học. Tia phân giác có nhiều ứng dụng trong các bài toán liên quan đến tam giác, đường tròn, đa giác và các hình khác.

Một số tính chất của tia phân giác là:

– Nếu một tia phân giác của một góc trong một tam giác cắt cạnh đối diện ở trung điểm, thì tam giác đó là tam giác cân. Ví dụ, trong tam giác ABC, nếu tia phân giác của góc A cắt BC ở D sao cho BD = DC, thì AB = AC.

– Nếu một tia phân giác của một góc trong một tam giác cắt đường tròn ngoại tiếp ở điểm nằm trên đường kính, thì tam giác đó là tam giác vuông. Ví dụ, trong tam giác ABC, nếu tia phân giác của góc A cắt đường tròn ngoại tiếp ở E sao cho AE là đường kính, thì ABC là tam giác vuông cân tại A.

– Nếu ba tia phân giác của ba góc trong một tam giác cắt nhau ở một điểm, thì điểm đó là trung tâm của đường tròn nội tiếp tam giác. Ví dụ, trong tam giác ABC, nếu ba tia phân giác của ba góc A, B và C cắt nhau ở I, thì I là trung tâm của đường tròn nội tiếp tam giác ABC.

– Nếu bốn tia phân giác của bốn góc trong một tứ giác lồi cắt nhau ở một điểm, thì tứ giác đó là tứ giác nội tiếp. Ví dụ, trong tứ giác ABCD lồi, nếu bốn tia phân giác của bốn góc A, B, C và D cắt nhau ở O, thì ABCD là tứ giác nội tiếp.

2. Tia phân giác của một góc:

Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau. Ví dụ, nếu tia Oz là tia phân giác của góc xOy, thì ∠xOz = ∠yOz = ½∠xOy . Đường thẳng chứa tia phân giác của một góc gọi là đường phân giác của góc đó.

Tia phân giác của một góc có thể được vẽ bằng cách dùng thước và compa như sau:

– Dùng compa đo bán kính bất kỳ, chấm lên hai cạnh của góc để được hai điểm A và B.

– Dùng compa đo độ dài AB, chấm lên cạnh Ox để được điểm C sao cho AC = AB.

– Dùng compa đo độ dài AC, vạch trên cạnh Oy để được một vòng tròn tâm C bán kính AC.

– Giao điểm D của vòng tròn và cạnh Oy là điểm nằm giữa hai cạnh của góc xOy.

– Dùng thước kẻ tia OD. Tia OD là tia phân giác của góc xOy.

Tia phân giác của một góc có thể được áp dụng trong các bài toán liên quan đến hình học, đặc biệt là các bài toán về tam giác cân, tam giác đều, đường trung tuyến, đường cao và đường phân giác trong tam giác.

3. Định lý về tính chất các điểm thuộc tia phân giác:

Định lý về tính chất các điểm thuộc tia phân giác là một định lý quan trọng trong hình học Euclid. Định lý này có hai hướng: thuận và đảo.

– Định lý thuận nói rằng: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó. Nghĩa là, nếu M là một điểm trên tia phân giác Ot của góc xOy, thì khoảng cách từ M đến Ox bằng khoảng cách từ M đến Oy.

– Định lý đảo của tia phân giác là một định lý trong hình học, nói rằng nếu một điểm nằm bên trong một góc và cách đều hai cạnh của góc đó thì nó nằm trên tia phân giác của góc đó. Định lý này là đảo của định lý thuận, nói rằng nếu một điểm nằm trên tia phân giác của một góc thì nó cách đều hai cạnh của góc đó.

Để chứng minh định lý đảo của tia phân giác, ta có thể sử dụng các tính chất của tỉ lệ thức và định lý Ta-let. Giả sử trong tam giác ABC, có điểm D thuộc AB và điểm E thuộc AC sao cho AD/DB = AE/EC. Khi đó, ta có thể kẻ DE song song với BC và chứng minh được rằng DE là tia phân giác của góc A.

Một ứng dụng của định lý đảo của tia phân giác là để xác định vị trí của tâm trọng tâm G của tam giác. Ta biết rằng G là giao điểm của ba đường trung tuyến, mỗi đường trung tuyến chia cạnh đối diện thành hai phần bằng nhau. Do đó, G cũng là giao điểm của ba tia phân giác của các góc ở trung điểm các cạnh.

4. Các dạng bài tập phổ biến về tia phân giác của góc:

* Dạng 1: Tính góc chưa biết:

Bài 1: Cho tứ giác ABCD nội tiếp đường tròn (O), có AB = 6cm, BC = 8cm, CD = 10cm, DA = 12cm. Gọi I là giao điểm của hai tia phân giác của hai góc A và B. Tính góc ICD.

Lời Giải: Ta có tứ giác ABCD lồi, có I là giao điểm của hai tia phân giác của hai góc A và B. Áp dụng công thức trên, ta có:

IA/IB = AC/BD

IA/IB = 8/10

=> IA : IB = 4 : 5.

Do đó, tam giác IBC cân tại I, suy ra góc IBC bằng góc ICB bằng 36 độ. Do đường kính làm góc vuông, nên góc BCD bằng 90 độ. Vậy góc ICD bằng 90 – 36 = 54 độ.

Bài 2: Cho tam giác ABC vuông cân tại A, có AB = AC = 5cm. Gọi M là trung điểm của BC. Tính độ dài AM và góc BAM.

Lời Giải: Ta có tam giác ABC vuông cân tại A, có AM là tia phân giác của góc BAC. Áp dụng công thức trên, ta có:

AB/AM = BM/MC

5/AM = BM/2.5

=> AM = 10/3 cm.

Do tam giác ABC vuông cân, nên góc BAC bằng 90 độ chia đôi bằng 45 độ. Vậy góc BAM bằng 45 độ.

* Dạng 2: Tính cạnh chưa biết:

Bài tập:

Cho tam giác ABC vuông tại A, có AB = 3cm, AC = 4cm. Tính độ dài đoạn thẳng BD, biết D là trung điểm của cạnh huyền BC.

Lời Giải:

Ta có tam giác ABD vuông tại A, có AD là tia phân giác của góc BAC. Áp dụng công thức trên, ta có:

AB/AD = BD/DC

3/AD = BD/2

=> AD = 6cm và BD = 3cm.

* Dạng 3: Dạng bài chứng minh liên quan đến tia phân giác của góc

Phương pháp giải:

+ Dựa định lí về tia phân giác của một góc

+ Sử dụng khái niệm tia phân giác của một góc

Bài tập:

Cho góc mAn, kẻ EH vuông góc với Am, EK vuông góc với An. Biết Ap là tia phân giác của mAn, E thuộc Ap. Chứng minh rằng EH = EK

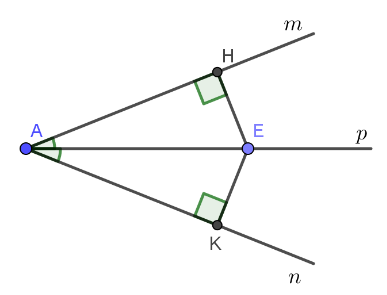
Lời Giải:

Vì Ap là tia phân giác của góc mAn, E thuộc Ap.

=> Khoảng cách từ E đến Am = khoảng cách từ E đến An

=> EH = EK (định lí)

4. Bài tập rèn luyện:

Bài 1: Cho tam giác ABC vuông ở A, có AB = 3 cm, AC = 4 cm. Tính độ dài của tia phân giác của góc B.

Lời giải:

– Gọi D là trung điểm của AC, E là giao điểm của BD và AB.

– Ta có tam giác ABD vuông cân ở D, nên BD = AD = 2 cm.

– Tam giác ABE vuông ở A, nên theo định lí Py-ta-go, ta có: BE^2 = AB^2 – AE^2 = 9 – 4 = 5 (cm^2).

– Vậy BE = √5 cm.

– Tam giác BDE cân ở D, nên DE = BD = 2 cm.

– Tam giác BCE vuông ở E, nên theo định lí Py-ta-go, ta có: BC^2 = BE^2 + CE^2 = 5 + (DE – CD)^2 = 5 + (2 – 2)^2 = 5 (cm^2).

– Vậy BC = √5 cm.

– Do đó, độ dài của tia phân giác của góc B là BC + BE = √5 + √5 = 2√5 cm.

Bài 2: Cho tam giác ABC có AB ≠ AC. Gọi I là trung điểm của BC, J là giao điểm của AI và AB, K là giao điểm của AI và AC. Chứng minh rằng JK là tia phân giác của góc BAC.

Lời giải:

– Ta có AI cắt BC tại trung điểm I, nên AI là trung trực của BC theo định lí huyền – cạnh.

– Do đó, tam giác ABI và tam giác ACI đều vuông cân ở I, nên AB = AC và ∠BAI = ∠CAI.

– Vậy JK song song với BC theo định lí hai góc bằng nhau.

– Mà JK cắt hai cánh của góc BAC, nên JK chia góc BAC thành hai góc bằng nhau theo định lí hai dòng song song cắt nhau.

– Vậy JK là tia phân giác của góc BAC.