Bài viết Công thức, cách tính Tỉ số lượng giác của góc nhọn gồm 2 phần: Lý thuyết và Bài tập áp dụng có lời giải chi tiết giúp học sinh dễ học, dễ nhớ, nắm vững công thức và biết cách làm bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán 9.
Mục lục bài viết
1. Cách tính tỉ số lượng giác của góc nhọn:
1.1. Công thức tính:
Để tính tỉ số lượng giác của góc nhọn, chúng ta cần nhớ công thức nói rằng tổng các góc trong một tam giác bằng với góc thẳng, tức là bằng 180 °:
α + β + γ = 180°
Làm thế nào để sử dụng công thức này? Nếu biết các góc theo tỷ lệ a: b: c, bạn có thể viết chúng là ax, bx, cx, trong đó x không xác định. Và, theo công thức trên, chúng ta thu được:
ax + bx + cx = 180 °
Từ đó, trước hết bạn có thể xác định x chưa biết, sau đó là các góc: ax, bx, cx.
1.2. Làm cách nào để tìm các góc thiếu trong tam giác bằng cách sử dụng tỷ lệ lượng giác?
Nếu biết các góc của tam giác theo tỷ lệ a: b: c và muốn xác định góc, ta thực hiện theo các bước sau:
– Viết ra các góc chưa biết là ax, bx, cx.
– Thiết lập phương trình tổng của góc là: ax + bx + cx = 180 °.
– Đơn giản hóa phương trình: (a + b + c)x = 180°.
– Tính x = 180°/(a + b + c).
– Sử dụng x để xác định các góc cần tìm là ax, bx, cx.
– Nếu bạn cần tìm tỷ lệ các cạnh, hãy sử dụng định luật sin.
Tỷ lệ góc bây giờ là 2: 3: 4.
Ví dụ 1:
Cho tỉ lệ các góc của một tam giác là 2:3:4.
Tính các góc.
Hướng dẫn trả lời:
– Viết các góc là 2x, 3x, 4x và viết phương trình cho tổng của chúng là: 2x + 3x + 4x = 180°.
– Sau khi đơn giản hóa, chúng ta thu được:
9x = 180 °
→ x = 20 °
Kết quả là:
2x = 40 °
3x = 60 °
4x = 80 °.
Như vậy các góc thiếu là 40 °, 60 °, 80 °.
Ví dụ 2:
Giả sử cho các góc theo tỷ lệ 1: 1: 2.
Tìm các góc.
Hướng dẫn trả lời:
– Chúng ta viết các góc là x, x, 2x.
– Vì tổng của chúng là 180 °, chúng ta viết được phương trình:
x + x + 2x = 180 °.
– Do đó, tìm được:
4x = 180 °
→ x = 45 °.
– Kết quả ta nhận được 2x = 90
Các góc thiếu là 45 °, 45 °, 90 °. Đặc biệt, đây là một tam giác vuông!
2. Công thức tính tỉ số lượng giác của góc nhọn:
2.1. Công thức tính:
Tỷ lệ lượng giác có thể được tính bằng cách lấy tỷ lệ của hai cạnh bất kỳ của tam giác vuông. Chúng ta tìm ra vế thứ ba bằng định lý Pythagoras, dựa trên số đo của hai vế còn lại. Chúng ta có thể sử dụng dạng viết tắt của tỷ lệ lượng giác để so sánh chiều dài của hai cạnh bất kỳ với góc trong đáy. Góc θ là một góc nhọn (θ < 90º) và nói chung được đo có tham chiếu đến trục x dương, theo hướng ngược chiều kim đồng hồ.
Cho góc nhọn θ, từ một điểm bất kì trên một cạnh của góc α, kẻ đường vuông góc với cạnh kia.
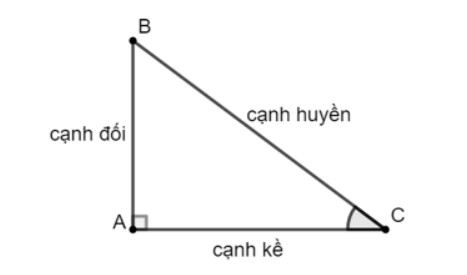
Các công thức tỷ lệ lượng giác cơ bản được đưa ra dưới đây:
sin θ = cạnh đối/cạnh huyền
cos θ = cạnh kề/cạnh huyền
tan θ = cạnh đối/cạnh kề
cot θ = cạnh kề/cạnh đối
Bây giờ, chúng ta hãy quan sát các công thức tỷ lệ lượng giác đối ứng của các tỷ lệ lượng giác nói trên. Khi quan sát, chúng ta nhận thấy rằng tan θ là đối của cot θ và cot θ là đối của tan θ. Vì vậy, bộ công thức mới cho tỷ lệ lượng giác là:
tan θ = 1/cot θ
cot θ = 1/tan θ
2.2. Bảng tỷ lệ lượng giác:
Trong bảng tỷ lệ lượng giác, chúng ta sử dụng các giá trị của tỷ lệ lượng giác cho các góc chuẩn 0 °, 30 °, 45 °, 60 ° và 90º. Thật dễ dàng để dự đoán các giá trị của bảng và sử dụng bảng làm tham chiếu để tính toán các giá trị của tỷ lệ lượng giác cho nhiều góc độ khác, sử dụng các công thức tỷ lệ lượng giác cho các mẫu hiện có trong tỷ lệ lượng giác và thậm chí giữa các góc. Dưới đây là bảng tóm tắt giá trị của tỷ lệ lượng giác cho các góc cụ thể:
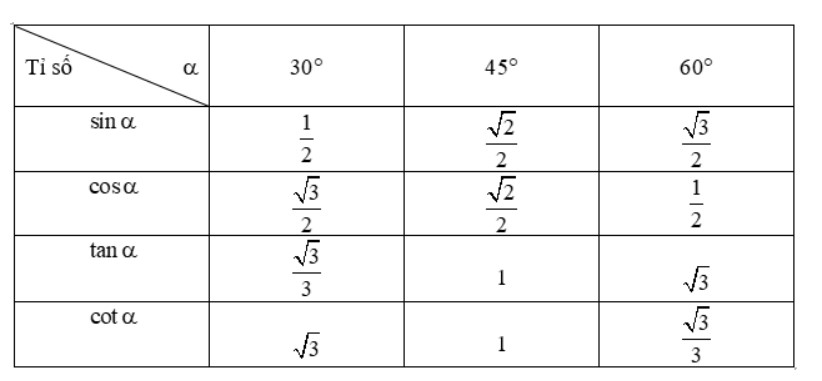
2.3. Công thức:
* Công thức đồng nhất về lượng giác của các góc bổ sung:
Các góc bổ sung là một cặp hai góc sao cho tổng của chúng bằng 90 °. Phần bổ sung của một góc θ là (90° – θ).
Tỷ lệ lượng giác của các góc bổ sung là:
sin (90°- θ) = cos θ
cos (90°- θ) = sin θ
cosec (90°- θ) = sec θ
sec (90°- θ) = cosec θ
tan (90°- θ) = cot θ
cot (90°- θ) = tan θ
* Công thức tính tỷ lệ tam giác Pythagore:
Các đồng nhất tỷ lệ lượng giác Pythagoras trong lượng giác có nguồn gốc từ định lý Pythagoras. Áp dụng định lý Pythagoras cho tam giác vuông dưới đây, chúng ta có:
(Cạnh đối)^2+ (Cạnh kề)^2 = (Cạnh huyền)^2
Chia cả hai vế cho (Cạnh huyền)^2:
(Cạnh đối)^2/(Cạnh huyền)^2
+ (Cạnh kề)^2/(Cạnh huyền)^2
= (Cạnh huyền)^2/(Cạnh huyền)^2
sin²θ + cos²θ = 1
Đây là một trong những tính chất quan trọng của định lí Pythagore.
Theo cách tương tự, chúng ta có thể rút ra công thức tỷ lệ lượng giác Pythagore khác:
sin²θ + cos²θ = 1
* Công thức đồng nhất về tổng, hiệu và tích của các tỷ lệ lượng giác:
Công thức đồng nhất về tổng, hiệu và tích của các tỷ lệ lượng giác bao gồm các công thức của sin (A + B), sin (A-B), cos (A + B), cos (A-B), v.v.
sin (A + B) = sin A cos B + cos A sin B
sin (A – B) = sin A cos B – cos A sin B
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
tan (A + B) = (tan A + tan B)/(1 – tan A tan B)
tan (A – B) = (tan A – tan B)/(1 + tan A tan B)
cot (A + B) = (cot A cot B – 1)/(cot B – cot A)
cot (A – B) = (cot A cot B + 1)/(cot B – cot A)
2 sin A⋅cos B = sin(A + B) + sin(A – B)
2 cos A⋅cos B = cos(A + B) + cos(A – B)
2 sin A⋅sin B = cos(A – B) – cos(A + B)
* Công thức đồng nhất nửa góc, góc kép và góc tam giác:
Công thức đồng nhất góc kép:
Các công thức tính tỷ lệ lượng giác mũ hai có thể thu được bằng cách sử dụng các công thức tổng và hiệu.
Ví dụ, từ công thức trên:
sin (A + B) = sin A cos B + cos A sin B
Thay thế A = B = θ ở cả hai bên, chúng ta nhận được:
sin (θ + θ) = sinθ cosθ + cosθ sinθ
sin2θ = 2 sinθ cosθ
Theo cách tương tự, chúng ta có thể rút ra các công thức sau:
sin 2θ = 2 sinθ cosθ
cos 2θ = cos²θ – sin²θ
cos 2θ = 2 cos²θ – 1
cos 2θ = 1 – 2 sin²θ
cos 2θ = (1 – tan² θ)/(1 + tan² θ)
tan 2θ = (2 tanθ)/ (1 – tan²θ)
cot 2θ = (cot θ – tan θ)/2
sec 2θ = sec2 θ/(2-sec2 θ)
cosec 2θ = (sec θ. cosec θ)/2
cot 2θ = (cot θ – tan θ)/2
* Công thức đồng nhất nửa góc:
Sử dụng một trong các công thức góc kép ở trên,
cos 2θ = 1 – 2 sin²θ
2 sin²θ = 1- cos 2θ
sin²θ = (1 – cos 2θ)/(2)
sin θ = ±√[(1 – cos 2θ)/2]
Thay thế θ bằng θ/2 ở cả hai bên,
sin (θ/2) = ±√[(1 – cos θ)/2]
Đây là công thức nửa góc của sin.
Theo cách tương tự, chúng ta có thể rút ra các công thức nửa góc khác.
sin (θ/2) =±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
tan (θ/2) = ±√[(1 – cos θ)(1 + cosθ)]
* Công thức đồng nhất góc tam giác:
sin 3θ = 3sin θ – 4sin³θ
cos 3θ = 4cos³θ – 3cos θ
tan 3θ = (3tanθ – tan³θ)/(1 – 3tan²θ)
3. Bài tập vận dụng có lời giải:
Bài 1: Cho tam giác ABC vuông tại C có BC = 0,9 cm, AC = 1,2 cm. Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc A.
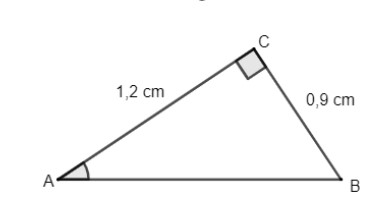
Hướng dẫn trả lời:
Áp dụng định lý Py – ta – go cho tam giác vuông ABC ta có:
AC2 + BC2 = AB2
⇔ 1,22 + 0,92 = AB2
⇔ 1,44 + 0,81 = AB2
⇔ 2,25 = AB2
=> AB = 1,5cm
Tỉ số lượng giác góc A là:

Bài 2: Cho tam giác ABC vuông tại A, đường cao AH, trung tuyến BM. Biết AB = 6, tan B = 12/5. Công thức Tỉ số lượng giác của góc nhọn. Hãy tính độ dài đường cao AH và trung tuyến BM.
Hướng dẫn trả lời:
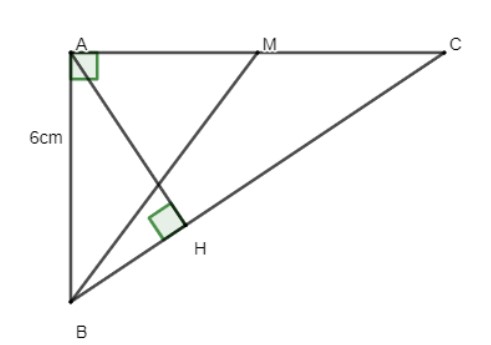
Áp dụng tỉ số lượng giác góc nhọn cho góc B của tam giác vuông ABC ta có:

Công thức Tỉ số lượng giác của góc nhọn
=> 5AC = 72
⇔ AC = 72 : 5
⇔ AC = 14,4cm
Vì BM là đường trung tuyến nên M là trung điểm của AC
=> MA = MC = 14,4 : 2 = 7,2 cm
Xét tam giác ABM vuông tại A ta có:
AB2 + BM2 = BM2(định lý py – ta – go)
⇔ 62 + 7,22 = BM2
⇔ BM2 = 87,84
=> BM ≈ 9,37cm
Xét tam giác ABC vuông tại A ta có:
AB2 + AC2 = BC2(định lý py – ta – go)
⇔ 62 + 14,22 = BC2
⇔ BC2 = 243,36
=> BC = 15,6cm
Áp dụng hệ thức lượng trong tam giác vuông cho tam giác vuông ABC ta có:
AB.AC = AH.BC
⇔ 6.7,2 = 14,4.AH
⇔ 43,2 = 14,4.AH
⇔ AH = 43,2 : 14,4
⇔ AH = 3cm
Bài 3: Không dùng máy tính hãy sắp xếp dãy sau theo thứ tự từ bé đến lớn:
Hướng dẫn trả lời:
a) tan 12⁰, cot 71⁰, cot 69⁰15′, tan 28⁰
b) sin32⁰, cos 51⁰, sin 39⁰, cos 45⁰
Hướng dẫn trả lời:
a) Vì 12⁰ và 78⁰ là hai góc phụ nhau nên tan 12⁰ = cot 78⁰
Vì 28⁰ và 62⁰ là hai góc phụ nhau nên tan 28⁰ = cot 62⁰.
Vì cot α < cot β ⇔ α > β
Ta có:
78⁰ > 71⁰ > 69⁰15′ > 62⁰
=> cot 78⁰ < cot 71⁰ < cot 69⁰15′ < cot 62⁰
=> tan 12⁰ < cot 71⁰ < cot 69⁰15′ < tan 28⁰
b) Vì 51⁰ và 39⁰ là hai góc phụ nhau nên cos 51⁰ < sin 39⁰
Vì 45⁰ và 45⁰ là hai góc phụ nhau nên cos 45⁰ = sin 45⁰
Vì sin α < sin β ⇔ α < β
Ta có:
32⁰ < 39⁰ < 45⁰
=> sin 32⁰ < sin 39⁰ < sin 45⁰
=> sin 32⁰ < sin 39⁰ = cos 51⁰ < cos 45⁰
THAM KHẢO THÊM:




