Cách tính khoảng cách giữa hai điểm trong hệ tọa độ

1. Cách tính khoảng cách giữa hai điểm trong hệ tọa độ:

1.1. Công thức tính khoảng cách giữa hai điểm: 

Khoảng cách giữa hai điểm trong hệ tọa độ đã cho có thể được tính bằng cách áp dụng công thức khoảng cách. Đối với bất kỳ điểm nào được cho trong mặt phẳng 2-D, chúng ta có thể áp dụng công thức khoảng cách 2D hoặc công thức khoảng cách Euclid, như sau: 

Công thức tính khoảng cách (d) giữa hai điểm có tọa độ là (x1,y1) và (x2, y2) là: 

d = √[(x2 − x1)2 + (y2 − y1)2]

Đây còn được gọi là Công thức khoảng cách Euclid.

Để tìm khoảng cách giữa các điểm có tọa độ (x1, y1, z1) và (x2, y2, z2) được cho trong mặt phẳng 3-D, chúng ta có thể áp dụng công thức khoảng cách 3D, như sau:

d = √[(x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2]

1.2. Dẫn xuất của công thức tính khoảng cách giữa hai điểm tọa độ:

Để rút ra công thức tính khoảng cách giữa hai điểm trong mặt phẳng hai chiều, chúng ta giả sử rằng có hai điểm với tọa độ được cho là, A (x1, y1) B (x2, y2). Tiếp theo, giả định rằng đoạn thẳng nối A và B là  = d. Sau đó, vẽ các điểm đã cho trên mặt phẳng tọa độ và nối chúng bằng một đường thẳng.

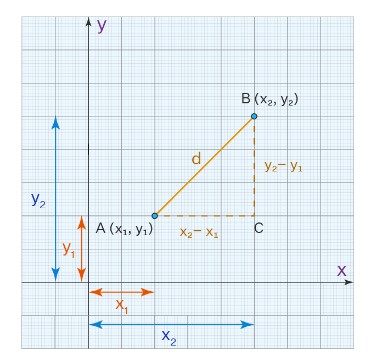
Tiếp theo, chúng ta vẽ một tam giác vuông với như cạnh huyền.

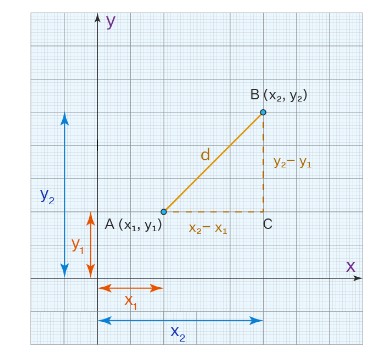
Áp dụng định lý Py ta go cho △ABC:

AB^2 = AC^2 + BC^2

d^2 = (x2 − x1)^2 + (y2 − y1)^2 (Giá trị từ hình)

Ở đây, khoảng cách thẳng đứng giữa các điểm đã cho là |y2 − y1|.

Khoảng cách ngang giữa các điểm đã cho là |x2 − x1|.

d = √[(x2 − x1)^2 + (y2 − y1)^2] (Lấy căn bậc hai ở cả hai bên)

Như vậy, công thức tìm khoảng cách giữa hai điểm đã được chứng minh.

Lưu ý: Trong trường hợp hai điểm A và B nằm trên trục x, tức là tọa độ của A và B lần lượt là (x1, 0) và (x2, 0), thì khoảng cách giữa hai điểm AB = |x2 − x1|.

Sử dụng các bước và cách tính tương tự, chúng ta cũng có thể rút ra công thức để tìm khoảng cách giữa hai điểm được đưa ra trong mặt phẳng 3D.

1.3. Làm thế nào để tìm ra khoảng cách giữa hai điểm tọa độ?

Khoảng cách giữa hai điểm trong hệ tọa độ đã cho có thể được tính toán với các bước sau đây:

– Ghi lại tọa độ của hai điểm đã cho trong mặt phẳng tọa độ là, A (x1, y1) và B (x2, y2).

– Chúng ta có thể áp dụng công thức khoảng cách để tìm khoảng cách giữa hai điểm

d = √[(x2 − x1)2 + (y2 − y1)2]

– Sau đó ta được đáp án.

Lưu ý: Có thể áp dụng công thức tính khoảng cách 3D trong trường hợp hai điểm được cho trong mặt phẳng 3D, d = √[(x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2]

* Ví dụ: Tìm khoảng cách giữa các điểm có tọa độ được cho là A = (1, 2) và B = (1, 5).

Hướng dẫn giải:

Khoảng cách giữa hai điểm được cho trong hệ tọa độ là 

d = √[(x2 − x1)2 + (y2 − y1)2] trong đó (x1, y1) và (x2, y2) là tọa độ của hai điểm.

⇒ d = √[(1 − 1)2 + (5 − 2)2]

⇒ d = 3 đơn vị

Từ ví dụ trên, chúng ta có thể quan sát thấy rằng khi tọa độ x của các điểm đã cho bằng nhau (tức là khi các điểm nằm trên một đường thẳng đứng), chúng ta có thể tìm khoảng cách giữa hai điểm bằng cách tìm giá trị tuyệt đối của sự khác nhau giữa các tọa độ y.

Theo cách tương tự, khoảng cách giữa hai điểm nằm trên một đường thẳng nằm ngang là giá trị tuyệt đối của sự khác biệt trong tọa độ x của chúng.

– Khoảng cách d giữa hai điểm có tọa độ là (x1,y1) và (x2, y2) là: 

d = √[(x2 − x1)2 + (y2 − y1)2]

– Chú ý rằng, không có vấn đề gì khi chúng ta trao đổi các giá trị x1 và x2 trong công thức này vì (x2 – x1)2 giống như (x1 – x2)^2. Điều tương tự cũng hoạt động với tọa độ y. Do đó, khoảng cách giữa hai điểm cũng có thể được viết là √[(x1 − x2)2 + (y1 − y2)2].

2. Khoảng cách giữa hai điểm trong mặt phẳng phức:

Khoảng cách giữa hai điểm trong một mặt phẳng phức được tính bằng cách sử dụng một công thức tương tự như khoảng cách giữa hai điểm công thức trong mặt phẳng Cartesian. Xét hai số phức z1 = a + ib và z2 = c + id. 

Mọi số phức trên một mặt phẳng phức tương ứng với một điểm trên mặt phẳng tọa độ. 

Khi đó khoảng cách giữa hai số phức z1 và z2 là:

|z1 − z2| = √[(a − c)2 + (b − d)2]

Ở đây |z1 − z2| là giá trị tuyệt đối của số phức z1 − z2.

* Ví dụ: Tìm khoảng cách giữa các số phức z1 = 1 + 3i và z2 = 2 – 4i.

Hướng dẫn giải:

Các điểm biểu thị cho các số phức đã cho là (1, 3) và (2, -4). 

Vì vậy, khoảng cách giữa các số phức là:

|z1 − z2| = √[(1 – 2)2 + (3 + 4)2 = √(1 + 49) = √50 = 5√2 đơn vị

Lưu ý: 

– Khoảng cách của một điểm (a, b):

(i) x – trục là |b|.

(ii) y – trục là |a|.

Sử dụng các dấu hiệu giá trị tuyệt đối vì khoảng cách không bao giờ có giá trị âm.

3. Bài tập tính khoảng cách giữa hai điểm trong hệ tọa độ:

Bài 1: Tìm khoảng cách giữa hai điểm (2, -6) và (7, 3) trong hệ tọa độ.

Hướng dẫn giải:

Chúng ta hãy giả sử các điểm đã cho là:

(x1,y1) = (2, -6)

(x2,y2) = (7,3)

Công thức để tìm khoảng cách giữa hai điểm là:

d = √[(x2 − x1)^2 + (y2 − y1)^2]

d = √[(7−2)^2 + (3−(−6))^2]

d = √(52 + 92)

d = √(25 + 81)

d = √106

Đáp án: Khoảng cách giữa hai điểm (2, -6) và (7, 3) trong hệ tọa độ d = √106.

Bài 2: Chỉ ra rằng các điểm (2, -1), (0, 1) và (2, 3) là các đỉnh của một tam giác vuông.

Hướng dẫn giải:

Chúng ta hãy giả sử các điểm đã cho là:

A = (2, −1)

B = (0, 1)

C = (2, 3)

Tìm chiều dài của mỗi cạnh của tam giác, công thức tính khoảng cách như sau: 

AB = √[(0−2)^2 + (1−(−1))^2]

= √[(−2)^2 + (2)^2]

= √(4 + 4)

= √8

BC = √[(2 − 0)^2 + (3 − 1)^2]

= √[(2)^2 + (2)^2]

= √(4 + 4)

= √8

CA = √[(2 − 2)^2 + (3−(−1))^2]

= √(0^2 + 4^2)

= √16

= 4

Bây giờ chúng ta đã biết độ dài của cả ba cạnh,

AB^2 + BC^2 = CA^2

(√8)^2 + (√8)^2 = 4^2

8 + 8 = 16

16 = 16

Do đó, A, B và C thỏa mãn định lý Pythagoras.

Vì vậy, △ABC là một tam giác vuông.

* Chúng ta có thể kiểm tra bằng cách đánh dấu tất cả các tọa độ trên biểu đồ:

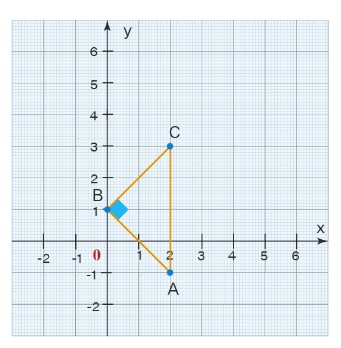
Bài 3: Tìm một điểm trên trục y trong hệ tọa độ cách đều các điểm (-1, 2) và (2, 3).

Hướng dẫn giải:

Chúng ta biết rằng tọa độ x của bất kỳ điểm nào trên trục y là 0.

Do đó, chúng ta giả định điểm cách đều các điểm đã cho là (0, k). 

Tức là,

Khoảng cách giữa (0, k) và (-1, 2) = Khoảng cách giữa (0, k) và (2, 3)

√[(−1 − 0)^2 + (2 − k)^2] = √[(2 − 0)^2 + (3 − k)^2]

Bình phương ở cả hai bên,

(−1 − 0)^2 + (2 − k)^2 = (2 − 0)^2 + (3 − k)^2

1 + 4 + k^2 − 4k = 4 + 9 + k^2 − 6k

2k = 8

k = 4

Do đó, điểm yêu cầu là (0, k) = (0, 4)

Đáp án: Điểm yêu cầu là (0, k) = (0, 4).