Trục căn thức ở mẫu của biểu thức (Bài tập Toán lớp 9)

1. Cách trục căn thức ở mẫu của biểu thức:

Để trục căn thức ở mẫu số của phân số, ta cần thực hiện các bước sau:

– Bước 1: Viết lại phân số dưới dạng a/b, trong đó a và b là hai đa thức.

– Bước 2: Tìm các ước chung của a và b, rút gọn phân số nếu có thể.

– Bước 3: Nếu b là một số hữu tỉ, ta nhân cả tử và mẫu cho căn bậc hai của b để trục căn thức ở mẫu.

– Bước 4: Nếu b là một biểu thức chứa căn bậc hai, ta nhân cả tử và mẫu cho biểu thức đồng dạng với b nhưng có dấu ngược lại. Ví dụ, nếu b = x + √y, ta nhân cả tử và mẫu cho x – √y. Sau đó, ta sử dụng công thức (a + b)(a – b) = a^2 – b^2 để loại bỏ căn thức ở mẫu.

– Bước 5: Kết quả cuối cùng là phân số có mẫu số là một số hữu tỉ không chứa căn thức.

* Lý thuyết trục căn thức ở mẫu:

* Lý thuyết trục căn thức ở mẫu của biểu thức:

2. Công thức trục căn thức ở mẫu:

3. Bài tập trục căn thức ở mẫu của biểu thức:

Bài 1:

a) Trục căn thức 

Hướng dẫn giải:

– Bước 1: Xác định căn trong mẫu số của biểu thức. Trong trường hợp này là

– Bước 2:  Xác định hệ số trục căn thức. Vì mẫu số chỉ là một căn bậc hai duy nhất, nên phần cần trục căn thức là

– Bước 3: Nhân phân số với hệ số trục căn thức. Điều này có nghĩa là chúng ta nhân cả tử số và mẫu số với Ta được như sau: .

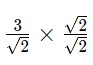Như vậy, đáp án cuối cùng là .

b) Trục căn thức

Hướng dẫn giải: 

– Bước 1: Mẫu số của biểu thức là

– Bước 2: Hệ số trục căn thức cũng chính là 

Lưu ý: chúng ta chọn bởi vì  khi nhân với chính nó, chúng ta nhận được 5, một số hữu tỉ, nhờ đó loại bỏ căn trong mẫu số.

– Bước 3: Nhân tử số và mẫu số với hệ số trục căn thức, ta được:

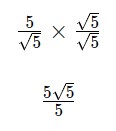
Đáp án cuối cùng là:

c) Trục căn thức

Hướng dẫn giải:

– Bước 1: Căn trong mẫu số là .

– Bước 2: Hệ số trục căn thức là . Chúng ta chọn bởi vì nhân lên bản thân  cho chúng ta 3, một số hữu tỉ, do đó loại bỏ căn khỏi mẫu số.

– Bước 3: Nhân tử số và mẫu số với hệ số trục căn thức, ta được:

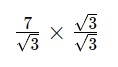
Đáp án cuối cùng là: .

Bài 2: 

Trục căn thức ở mẫu biểu thức với căn bậc ba tuân theo một quy trình tương tự như căn bậc hai. Tuy nhiên, có một sự khác biệt quan trọng.

Thay vì nhân với cùng một giá trị căn bậc hai ban đầu để có được một số hữu tỉ, chúng ta cần nâng gốc khối lên lũy thừa của 2. Bằng cách lũy thừa gốc, chúng ta loại bỏ căn khỏi mẫu số.

a) Trục căn thức ở mẫu biểu thức sau: .

Hướng dẫn giải: 

– Bước 1: Xác định căn trong mẫu số, là .

– Bước 2: Xác định hệ số trục căn thức. Trong trường hợp này, chúng ta cần căn bậc hai nâng lên lũy thừa 2 để có được một số hữu tỉ, vì vậy hệ số hợp lý hóa là .

– Bước 3: Nhân phân số với hệ số trục căn thức. Điều này có nghĩa là chúng ta nhân cả tử số và mẫu số với , ta được:

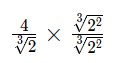
Đáp án cuối cùng là: .

b) Trục căn thức ở mẫu biểu thức sau: .

Hướng dẫn giải:

– Bước 1: Căn trong mẫu số là  .

– Bước 2: Hệ số trục căn thức là  Chúng ta chọn như vậy bởi vì nhân bản thân lên cho chúng ta 3, một số hữu tỉ, do đó loại bỏ căn khỏi mẫu số.

– Bước 3: Nhân tử số và mẫu số với hệ số trục căn thức, ta được:

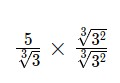
Đáp án cuối cùng là .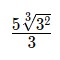

Bài 3: 

Trước khi chúng ta đi vào các bài tập, chúng ta hãy xem xét nhanh Quy tắc thương số của căn bậc hai.

Quy tắc thương số của căn bậc hai cho biết căn bậc hai của thương số bằng thương số của căn bậc hai của tử số và mẫu số. Nói cách khác, quy tắc này áp dụng đối với bất kỳ số thực dương nào a và b.

a) Trục căn thức ở mẫu biểu thức sau:

Hướng dẫn giải:

– Bước 1: Xác định phân số dưới căn và áp dụng Quy tắc thương số của căn bậc hai. Trong trường hợp này, phân số dưới căn là 1/2, và áp dụng Quy tắc thương số của căn bậc hai, chúng ta nhận được:

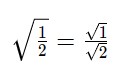
– Bước 2: Xác định hệ số trục căn thức. Trong trường hợp này, mẫu số là , vì vậy hệ số trục căn thức của chúng ta cũng là

– Bước 3: Nhân tử số và mẫu số với hệ số trục căn thức, ta được:

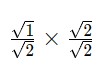
Đáp án cuối cùng là .

b) Trục căn thức ở mẫu biểu thức sau:  

Hướng dẫn giải:

– Bước 1: Phân số dưới căn là 3/5. Áp dụng Quy tắc thương số của căn bậc hai cho chúng ta: .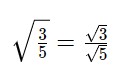

– Bước 2: Hệ số trục căn thức là , là căn bậc hai trong mẫu số.

– Bước 3: Nhân phân số với hệ số trục căn thức:

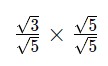
Đáp án cuối cùng là .

Tóm lại: bằng cách áp dụng Quy tắc thương số của căn bậc hai, chúng ta có thể đơn giản hóa vấn đề và làm theo các bước tương tự mà chúng ta đã sử dụng để trục căn thức ở mẫu của biểu thức.

Bài 4:

Khi chúng ta gặp mẫu số hai số hạng có chứa căn bậc hai, chúng ta sử dụng một chiến lược được gọi là “liên hợp” của nhị thức.

Trong toán học, liên hợp của nhị thức là một biểu thức hai số hạng giống hệt với bản gốc, ngoại trừ dấu giữa các số hạng bị đảo ngược.

Ví dụ: liên hợp của là  và ngược lại. Sự kỳ diệu của liên hợp nằm ở phép nhân của chúng: tích của nhị thức và liên hợp của nó luôn tạo ra giá trị bình phương khác biệt, nhờ đó loại bỏ căn bậc hai khỏi mẫu số.

Khi trục căn thức ở mẫu biểu thức có chứa hai số hạng, chúng ta sẽ tuân theo quy trình các bước tương tự như các bài tập trên, nhưng với một sự thay đổi trong bước thứ hai. Thay vì chỉ sử dụng căn bậc hai trong mẫu số làm hệ số trục căn thức, chúng ta sẽ sử dụng liên hợp của toàn bộ mẫu số. 

a)  Trục căn thức ở mẫu biểu thức sau:

Hướng dẫn giải:

– Bước 1: Xác định mẫu số để trục căn thức. Ở đây, mẫu số là

– Bước 2: Xác định hệ số trục căn thức. Trong trường hợp này, đó là liên hợp của mẫu số, đó là

– Bước 3: Nhân phân số với hệ số trục căn thức, nhớ nhân cả tử số và mẫu số: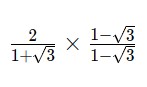

Đầu tiên, chúng ta nhân tử số:

Tiếp theo, chúng ta nhân các mẫu số, là các liên hợp, để có được sự khác biệt của các căn: .

Đặt nó lại với nhau, chúng ta nhận được , đơn giản hóa thành: .

Đáp án cuối cùng là .

b) Trục căn thức ở mẫu biểu thức sau:

Hướng dẫn giải:

– Bước 1: Xác định mẫu số để trục căn thức. Ở đây, mẫu số là

– Bước 2: Xác định hệ số trục căn thức. Trong trường hợp này, đó là liên hợp của mẫu số, đó là 4 +

– Bước 3: Nhân phân số với hệ số trục căn thức, nhớ nhân cả tử số và mẫu số: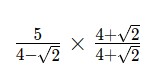

Đầu tiên, chúng ta nhân tử số: .

Tiếp theo, chúng ta nhân các mẫu số, là các liên hợp, để có được sự khác biệt của các căn: .

Đặt nó lại với nhau, chúng ta nhận được , đơn giản hóa thành: .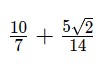

Đáp án cuối cùng là .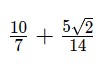

Bài 5: Trục căn thức ở mẫu biểu thức sau:

Hướng dẫn giải:

– Đảo ngược dấu giữa các số hạng của mẫu số để có được liên hợp của nó. Điều đó có nghĩa là, liên hợp của ​ là

– Nhân cả tử và mẫu với liên hợp, ta được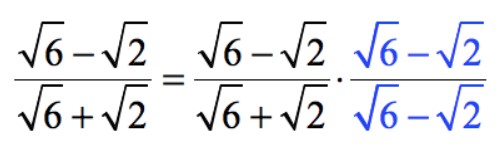

– Các số hạng giữa của tử số sẽ được thêm vào, trong khi các số hạng giữa của mẫu số sẽ bị hủy.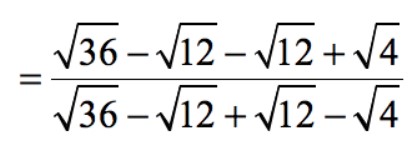

– Đơn giản hóa gốc của số bình phương. Cộng hoặc trừ toàn bộ các số xuất hiện sau khi nhận được căn bậc hai của các số bình phương.

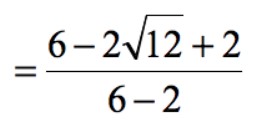
– Lúc này, hãy đơn giản hóa √(12). Hãy nhớ chia nhỏ như một sản phẩm trong đó một trong những yếu tố của nó là một số bình phương hoàn hảo.

– Rõ ràng 12 = 4 × 3. Đây là một sự lựa chọn hoàn hảo của các số hạng vì 4 là một căn bậc hai hoàn hảo.

– Chúng ta biết rằng căn bậc hai của 4 bằng 2.

– Đơn giản hóa bằng phép nhân .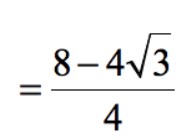

– Tử số có một yếu tố chung là 4. Chúng ta có thể rút 4 ra ngoài ngoặc đơn.

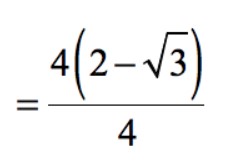
– Hủy bỏ các yếu tố chung giữa tử số và mẫu số, ta được