Phương trình tiếp tuyến song song với một đường thẳng là kiến thức rất quan trọng trong Toán học lớp 11. Bài viết dưới đây với chủ đề Các dạng bài tập về tiếp tuyến lớp 11 và cách giải sẽ giúp học sinh nắm vững lý thuyết, biết cách làm bài tập từ đó có kế hoạch ôn tập hiệu quả để đạt kết quả cao trong các bài thi môn Toán 11.
Mục lục bài viết
1. Lý thuyết phương trình tiếp tuyến song song với một đường thẳng:
– Đạo hàm của hàm số y = f(x) tại điểm x0 là hệ số góc của tiếp tuyến với đồ thị (C) của hàm số tại điểm M0(x0; f(x0)).
– Khi đó phương trình tiếp tuyến của (C) tại điểm M0 (x0; f(x0)) là:
y = f’(x0) . (x – x0) + y0
2. Cách viết phương trình tiếp tuyến song song với một đường thẳng:
Dạng 1. Tiếp tuyến tại một điểm thuộc đồ thị:
* Phương pháp giải:
Phương trình tiếp tuyến với đồ thị (C): y = f(x) tại điểm M0 (x0; f(x0)) là:
y = f’(x0) . (x – x0) + f(x0)
Trong đó:
– M0 (x0; y0) gọi là tiếp điểm.
– k = f'(x0) là hệ số góc.
* Chú ý:
– Nếu cho x0 thì thế vào y = f(x) tìm y0.
– Nếu cho y0 thì thế vào y = f(x) tìm x0
Dạng 2. Tiếp tuyến biết hệ số góc:
* Phương pháp giải:
– Bước 1: Gọi M (x0; f(x0)) là tọa độ tiếp điểm của tiếp tuyến của (C) thì f'(x0) = k
– Bước 2: Giải phương trình f'(x0) = k với ẩn là x0.
– Bước 3: Phương trình tiếp tuyến của (C) có dạng y = k(x – x0) + f(x0).
* Chú ý:
Cho hai đường thẳng: d1 : y = a1x + b1 và d2 : y = a2x + b2, với a1, a2 lần lượt là hệ số góc của d1 và d2. Khi đó:
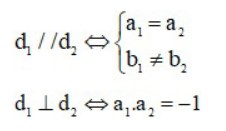
* Hệ số góc của đường thẳng (d) y = ax + b là: kd = a = tanα với α là góc nằm bên trên trục hoành tạo bởi đường thẳng (d) và chiều dương của trục Ox.
– Khi a > 0, ta có kd = tanα = a.
– Khi a < 0, ta có kd = tan(180° − α).
Dạng 3. Tiếp tuyến đi qua một điểm:
* Phương pháp giải:
– Bước 1:
Gọi tọa độ tiếp điểm của tiếp tuyến d là M (x0; f(x0)). Tính y’ = f'(x).
Hệ số góc của tiếp tuyến d là k = f'(x0).
Phương trình đường thẳng d: y = f'(x0) . (x – x0) + f(x0).
– Bước 2:
Do đường thẳng d đi qua điểm A (xA; yA)
Nên yA = f'(x0)(xA – x0) + f(x0). Phương trình đưa về ẩn x0 . Giải phương trình tìm x0.
– Bước 3:
Với x0 tìm được, quay lại dạng 2 .Từ đó viết phương trình d.
* Chú ý:
– Nếu bài toán chỉ cho x0 thì ta cần tìm y0 = f(x0) và f’(x0).
– Nếu bài toán chỉ cho y0 thì ta cần tìm x0 bằng cách giải phương trình f(x) = y0.
– Giá trị f’(x0) là hệ số góc của tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M (x0; y0).
3. Bài tập vận dụng liên quan kèm lời giải:
Câu 1: Cho hàm số y = f(x) = ⅓.x³ – ½.x² + 1 có đồ thị (C), viết phương trình tiếp tuyến của (C) biết : Tiếp tuyến song song với đường thẳng (d’): y = 2020.
Lời giải chi tiết:
Gọi k là hệ số góc của tiếp tuyến của đồ thị (C).
Do tiếp tuyến song song với (d’) : y = 2020 với hệ số góc k = 0
→ k = 0
Gọi M (x0; y0) là điểm thuộc đồ thị (C) mà tiếp tuyến của (C) tại M có hệ số góc k = 0
→ f’(x0) = 0 ⇔ x0² – x0 = 0 ⇔ x⁰ = 0 hoặc x⁰ = 1
* Với x0 = 0 ta có y0 = f(0) = 1 ⇒ M1 (0;1) ∈ (C).
Phương trình tiếp tuyến của (C) tại M1(0; 1) là y = 1.
* Với x0 = 1 ta có y0 = f(1) = ⅚ → M2 (1; ⅚) ∈ (C)
Phương trình tiếp tuyến của (C) tại M2 (1; ⅚) là y = ⅚.
Câu 2: Viết phương trình tiếp tuyến cho đồ thị hàm số y = x² – 2x – 1 song song với đường thẳng y = 2x – 1.
Lời giải chi tiết:
Chúng ta thực hiện các bước sau:
– Nhận thấy rằng hệ số góc của đường thẳng là k = 2.
– Tìm đạo hàm của hàm số: f'(x) = 2x – 2.
– Giải phương trình 2x – 2 = 2 để tìm x0, ta được x0 = 2.
– Tính y0 = f(2) = 2² – 2.2 – 1 = -1.
– Viết phương trình tiếp tuyến: y – (-1) = 2(x – 2), đơn giản hóa ta được y = 2x – 5.
Câu 3: Cho hàm số y = x³ + 3x – 1 và đường thẳng y = 6x – 1. Tìm tiếp tuyến của hàm số song song với đường thẳng đã cho.
Lời giải chi tiết:
– Chúng ta cần tìm hệ số góc k của đường thẳng, trong trường hợp này là k = 6.
– Sau đó, chúng ta tìm đạo hàm của hàm số, f'(x) = 3x² + 3, và giải phương trình 3x² + 3 = 6 để tìm hoành độ tiếp điểm x0.
– Phương trình này có hai nghiệm là x1 = 1 và x2 = -1.
– Tính tung độ tương ứng tại hai điểm này trên đồ thị hàm số, ta được y1 = f(1) = 3 và y2 = f(-1) = -5.
– Cuối cùng, viết phương trình tiếp tuyến tại hai điểm tiếp xúc: y = 6(x – 1) + 3 cho điểm M1(1; 3) và y = 6(x + 1) – 5 cho điểm M2(-1; -5).
Như vậy, chúng ta có hai phương trình tiếp tuyến song song với đường thẳng y = 6x – 1 là y = 6x – 3 và y = 6x + 1.
Câu 4: Cho đồ thị hàm số y = f(x) = 4x – 3/x – 1. Viết phương trình tiếp tuyến (∆) của (C) biết (∆) song song với đường thẳng (d): 4x + y – 5 = 0.
Lời giải chi tiết:
Gọi k là hệ số góc của tiếp tuyến (∆).
(d): 4x + y − 5 = 0 ⇒ y = −4x + 5
Do tiếp tuyến (∆) song song với đt (d) ⇒ k = −4
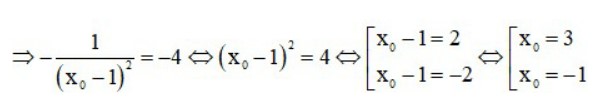
* Với x0 = 3 ta có y0 = f(3) = (4.3 – 3)/4 – 1 = 3 ⇒ M1(3;3).
Phương trình tiếp tuyến (∆): y = −4.(x − 3) + 3 ⇔ y = −4x +15
* Với x0 = – 1 ta có 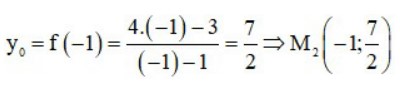
Phương trình tiếp tuyến (∆) y = −4 . (x + 1) + 7/2 ⇔ y = −4x − ½.
Câu 5: Tìm một phương trình đường thẳng tiếp tuyến với đồ thị của f và song song với đường thẳng đã cho.
Đồ thị: f(x) = 2x²
Đường thẳng: 2x – y + 5= 0
Lời giải chi tiết:
Độ dốc của tiếp tuyến với một đường cong tại bất kỳ điểm cụ thể nào được cho bởi đạo hàm của đường cong tại điểm đó.
Chúng ta có:
f(x) = 2x²
Chúng ta có:
f'(x) =4x
Bây giờ nếu lấy phương trình đường đã cho và đặt nó thành dạng chuẩn y = mx + c:
2x − y + 5 = 0
⇒y = 2x − 5
Vì vậy, độ dốc của đường thẳng này là:
m = 2
Nếu chúng ta muốn phương trình tiếp tuyến của song song với đường thẳng này thì nó phải có cùng độ dốc, do đó:
f'(x) = 2
⇒4x = 2
x =½
Khi x = 1/2
⇒f(x) = 2 ⋅1/4 = 1/2
Vì vậy, tiếp tuyến đi qua (½;1/2) và có độ dốc mT = 2, sử dụng biểu thức y − y1 = m. (x − x1)
Phương trình tiếp tuyến mà chúng ta tìm kiếm là
y – ½ = 2 . (x – ½)
→ y – ½ = 2x – 1
→ y = 2x – ½
Câu 6: Cho hàm số y = x3 – 2×2 + (m – 1) x + 2m có đồ thị (Cm). Giá trị thực của tham số m để tiếp tuyến của đồ thị (Cm) tại điểm có hoành độ x = 1 song song với đường thẳng y = 3x + 10 là?
Lời giải chi tiết:
Có y’ = 3×2 – 4x + m – 1 ⇒ y’ (1) = m – 2.
Tiếp tuyến của (Cm) tại điểm có hoành độ x = 1 có phương trình là
y = (m – 2) (x – 1) + 3m – 2 ⇔ y = (m – 2) x + 2m
Do tiếp tuyến song song với đường thẳng y = 3x + 10 nên m – 2 = 3 và 2m ≠ 10 (vô lí)
Vậy không tồn tại m thỏa mãn yêu cầu bài toán.
Câu 7: Phương trình tiếp tuyến của đồ thị hàm số y = x3 – 3x + 1 song song với trục Ox là?
Lời giải chi tiết:
Do tiếp tuyến song song với trục Ox nên tiếp tuyến có tiếp điểm là các điểm cực trị và có phương trình y = y0 với y0 là giá trị cực trị của hàm số đã cho.
Ta có y’ = 3×2 – 3; y’ = 0 ⇔ x = ±1.
Do hàm số đã cho là hàm bậc ba nên các điểm cực trị là A (1; -1), và B (-1; 3).
Vậy phương trình các đường tiếp tuyến cần tìm là y = -1; y = 3.
THAM KHẢO THÊM: