Phương trình tiếp tuyến của đường cong là một phương trình xác định đường thẳng tiếp xúc với đường cong tại một điểm cụ thể trên đường cong đó. Đường thẳng tiếp tuyến này có đặc điểm là có cùng đạo hàm như đường cong tại điểm tiếp xúc đó. Dưới đây là bài viết hướng dẫn viết phương trình tiếp tuyến của đường cong.
Mục lục bài viết
1. Cách viết phương trình tiếp tuyến của đường cong:
Dạng 1. Phương trình tiếp tuyến của đường cong (C): tại tiếp điểm M có dạng:
d: y = f’(x0) . (x – x0) + y0
Áp dụng trong các trường hợp sau:
| Trường hợp | Cần tìm | Ghí chú |
| 1. Viết phương trình tiếp tuyến d của (C) tại điểm M (x0; y0). | Hệ số góc : f’(x0) |
|
| 2. Viết phương trình tiếp tuyến d của (C) tại điểm có hoành độ x = x0. | Hệ số góc : f’(x0) Tung độ tiếp điểm: y = f(x0) | Từ: x0 → f’(x0) và f(x0) |
| 3. Viết phương trình tiếp tuyến d của (C) tại điểm có tung độ ý = y0. | Hoành độ tiếp điểm: x0 Hệ số góc: f’(x0) | Giải phương trình: y0 = f(x0)
|
| 4. Viết phương trình tiếp tuyến d của (C), biết hệ số góc k của tiếp tuyến d. | Hoành độ tiếp điểm: x0 Tung độ tiếp điểm: y0 = f(x0) | Giải phương trình: f’(x0) = k
|
* Chú ý: Gọi k1 là hệ số góc của đường thẳng d1 và k2 là hệ số góc của đường thẳng d2.
– Nếu d1 song song với d2 thì k1 = k2.
– Nếu d1 vuông góc với d2 thì k1 . k2 = -1
Dạng 2. Viết phương trình tiếp tuyến của đường cong (C) đi qua điểm A (x1; y1)
Phương pháp:
– Bước 1: Viết phương trình đường thẳng d đi qua điểm A và có hệ số góc k
d: y = k(x – x1) + y1
– Bước 2. Tìm điều kiện để d là tiếp tuyến của đường cong (C) :
d tiếp xúc với đường cong (C) : ⇔ f(x) = k(x – x1) + y1 và f’(x) = k (*) có nghiệm.
– Bước 3: Khử k, tìm x, thay x vào (*) để tìm k, từ đó suy ra các tiếp tuyến cần tìm.
2. Bài tập vận dụng liên quan:
Câu 1: Cho đường cong y = x³. Tìm tiếp tuyến qua điểm (1; 2).
Lời giải chi tiết:
– Tính đạo hàm của y = x³, ta được f'(x) = 3x².
– Tính hệ số góc tại điểm (1; 2) bằng cách thay x = 1 vào đạo hàm, ta được f'(1) = 3.
– Viết phương trình tiếp tuyến sử dụng điểm đã cho và hệ số góc: y – 2 = 3 . (x – 1).
– Rút gọn phương trình để có dạng chuẩn: y = 3x – 1.
Phương trình tiếp tuyến này cho ta biết rằng tại điểm (1; 2), đường thẳng tiếp xúc với đường cong y = x³ có độ dốc là 3 và cắt trục tung tại điểm có tọa độ y = -1.
Câu 2: Có đường cong với phương trình y = x² + 3x – 2. Tìm phương trình tiếp tuyến tại điểm M(2; 9).
Lời giải chi tiết:
– Đầu tiên, chúng ta cần tính đạo hàm của hàm số để xác định hệ số góc của tiếp tuyến.
Đạo hàm của y = x² + 3x – 2 là y’ = 2x + 3.
– Tiếp theo, chúng ta tính hệ số góc tại điểm M bằng cách thay x = 2 vào đạo hàm, ta được y'(2) = 7.
– Với hệ số góc m = 7, chúng ta viết phương trình tiếp tuyến dựa trên công thức y – y1 = m(x – x1), với (x1; y1) là tọa độ của điểm M.
– Thay các giá trị vào, ta được phương trình tiếp tuyến là y – 9 = 7(x – 2), và sau khi rút gọn, ta có phương trình tiếp tuyến cuối cùng là y = 7x – 5.
Phương trình này cho biết tiếp tuyến tại điểm M(2; 9) có độ dốc là 7 và cắt trục tung tại điểm có tọa độ y = -5.
Câu 3: Cho hàm số y = x³ – 3x² + 2x + 5 (C) . Viết phương trình tiếp tuyến tại điểm có x = 1.
Lời giải chi tiết:
Với x = 1
→ y = – 4
→ M (1; -5) ∈ C
y = 3×2 – 6x + 2 → y(1) = -1
Vậy tiếp tuyến tại M có dạng: y = – 1(x – 1) – 5 ⇔ y = – x – 4.
3. Bài tập nâng cao kèm lời giải:
Câu 1: Chứng minh rằng trong số các tiếp tuyến của đồ thị hàm số bậc ba y = f(x) = ax³ + bx² + cx +d, với a > 0, tiếp tuyến tại điểm x0 sao cho f”(x0) = 0 là tiếp tuyến có hệ số góc nhỏ nhất.
Lời giải chi tiết:
Ta có:
f’(x) = 3ax² + 2bx + c
f’(x) = 6ax + 2b
Nên
f’(x0) = 0 ⇔ x0 = -b/3a
Hệ số góc của tiếp tuyến tại điểm x0 này là
f’(x0) = -b²/3a + c
Hệ số góc của tiếp tuyến tại điểm x bất kì là
f'(x) = 3ax² + 2bx + c
Như vậy, ta cần chứng minh rằng với mọi x, ta phải có
-b²/3a + c <= 3ax² + 2bx + c, hay
3ax² + 2bx + b²/3a >=0
⇔ 9a²x² + 6abx + b² >= 0
⇔ (3ax + b)² >= 0 (đúng)
Câu 2: Cho hàm số y = x³ – 3x² + 2 có đồ thị (C). Viết phương trình tiếp tuyến của (C) đi qua điểm A(-1;-2).
Lời giải chi tiết:
Gọi tiếp điểm là M0 (x0; y0) với y0 = x0³ – 3×0² + 2 thì phương trình tiếp tuyến là
y = (3×0² – 6×0) . (x – x0) + x0³ – 3×0² + 2 (1)
Tiếp tuyến đi qua điểm A (-1; -2), suy ra
-2 = (3×0² – 6×0) . (- 1 – x0) + x0³ – 3×0² + 2 (1)
Phương trình có 2 nghiệm x0 = -1 và x0 = 2. Thế vào (1) ta có 2 tiếp tuyến với phương trình là y = 9x + 7 và y = – 2.
Câu 3: Cho hàm số y = x³ – 3x² + 4 có đồ thị (C). Viết phương trình đường thẳng (d) đi qua điểm A (-1; 0) và có hệ số góc k. Tìm các giá trị của k để (C) tiếp xúc với (d).
Lời giải chi tiết:
Ta có y’ = 3x² – 6x.
Phương trình đường thẳng (d): y = k(x + 1).
(d) tiếp xúc với (C) ⇔ Tồn tại điểm M (x0; y0)
Thỏa mãn hệ điều kiện sau:
y0 = k . (x0 + 1) = x0³ – 3×0² + 4 (1)
k = 3×0² – 6×0 (2)
(Điểm M (x0; y0) chính là tiếp điểm của (d) và (C)).
Thay (2) lên (1) và rút gọn ta được:
x³ – 3x – 2 = 0 ⇔ x0 = -1, x0 = 2
• x0 = -1 ⇒ k = 9
• x0 = 2 ⇒ k = 0
Vậy (d) tiếp xúc với (C) khi k = 0 hoặc k = 9.
Câu 4: Cho điểm A (x0; y0) thuộc đồ thị (C) của hàm số y = x3 – 3x + 1.
Tiếp tuyến với (C) tại A cắt (C) tại điểm B khác A. Tìm hoành độ điểm B theo x0.
Lời giải chi tiết:
Miền xác định của hàm số: D = R. Ta có: y’ = 3x² – 3.
Phương trình tiếp tuyến tại A:
y – x0³ + 3×0 – 1 = (3×0² – 3) . (x – x0) (D).
Phương trình hoành độ giao điểm của (D) và (C) là:
x3 – 3x + 1 – x0³ + 3×0 – 1 – (3×0² – 3) . (x – x0) = 0
⇔ x³ – 3x + 1 – x0³ + 3×0 – 3×0².x + 3×0³ + 3x – 3×0 =0
⇔ x³ – x0³ – 3×0².x + 3×0³ = 0
⇔ (x – x0) . (x² + x0.x – 2×0²) = 0
Phương trình bậc hai x² + x0.x – 2×0² cho ta hai nghiệm x0 và -2.×0
Vậy B có hoành độ là -2.x0.
Câu 5: Cho hàm số: y = 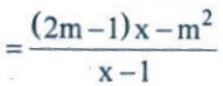 (1) (m là tham số). Tìm m để đồ thị của hàm số (1) tiếp xúc với đường thẳng y = x.
(1) (m là tham số). Tìm m để đồ thị của hàm số (1) tiếp xúc với đường thẳng y = x.
Lời giải chi tiết:
Kí hiệu: f(x) = 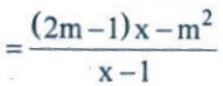 . Yêu cầu bài toán tương đương với tìm m để hệ phương trình sau có nghiệm :
. Yêu cầu bài toán tương đương với tìm m để hệ phương trình sau có nghiệm :
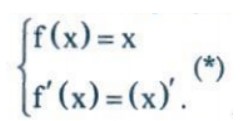
Ta có:
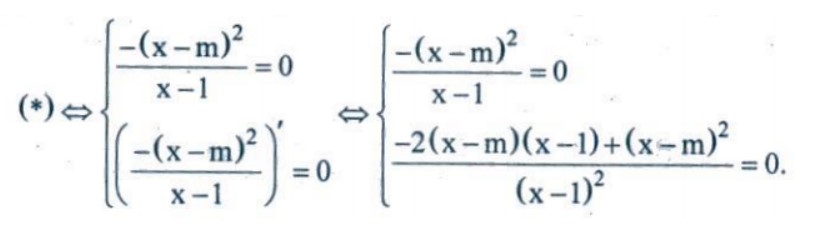
Ta thấy với mọi m ≠ 1, x = m luôn thỏa mãn hệ (*). Vì vậy với mọi m ≠ 1, (*) luôn có nghiệm, đồng thời khi m = 1 thì hệ (*) vô nghiệm. Do đó đồ thị hàm số (*) tiếp xúc với đường thẳng y = x khi và chỉ khi m ≠ 1.
Câu 6: Trên đồ thị của hàm số y = x² lấy hai điểm A, B có hoành độ là a, b (a < b). Hãy tìm điểm C trên cung AB mà tiếp tuyến tại đó song song với đường thẳng AB.
Lời giải chi tiết:
Hệ số góc của đường thẳng AB là 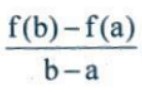 . Do đó, hoành độ của C phải thỏa mãn
. Do đó, hoành độ của C phải thỏa mãn 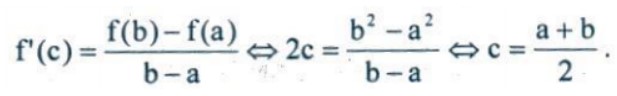
Phương trình tiếp tuyến tại C là 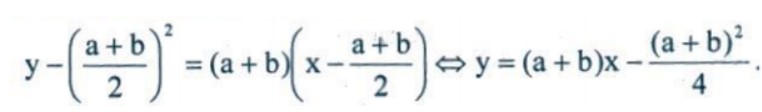
THAM KHẢO THÊM: