Hệ thức lượng trong tam giác là một phần quan trọng của hình học. Chúng giúp chúng ta tính toán các độ dài cạnh và góc trong tam giác dựa trên các thông tin đã biết. Dưới đây là bài viết với chủ đề Hệ thức lượng trong tam giác: Toán 10 Kết nối tri thức Bài 6. Xin mời các em học sinh cùng theo dõi.
Mục lục bài viết
1. Bài toán mở đầu:
Mở đầu trang 38 Toán 10 Tập 1:
Ngắm tháp rùa từ bờ, chỉ với những dụng cụ đơn giản, dễ chuẩn bị, ta cũng có thể xác định được khoảng cách từ vị trí ta đứng tới Tháp Rùa. Em có biết vì sao?
Lời giải chi tiết:
Theo các bước sau, ta có thể xác định được khoảng cách từ vị trí A trên bờ hồ Hoàn Kiếm đến Tháp Rùa.
– Bước 1. Trên bờ, đặt một cọc tiêu tại vị trí A và một cọc tiêu tại vị trí B nào đó. Đo khoảng cách AB.
– Bước 2. Đứng tại A, ngắm Tháp Rùa và một cọc tiêu tại ví trí B nào đó để đo góc tạo bởi hai hướng ngắm đó.
– Bước 3. Đứng tại B, ngắm Tháp Rùa và một cọc tiêu tại ví trí A để đo góc tạo bởi hai hướng ngắm đó.
– Bước 4. Gọi C là vị trí của Tháp Rùa. Áp dụng định lí sin cho tam giác ABC để tính độ dài cạnh AC.
2. Định lý cosin:
HĐ1 trang 38 Toán 10 Tập 1:
Một tàu biển xuất phát từ cảng Vân Phong (Khánh Hòa) theo hướng đông với vận tốc 20km/h. Sau khi đi được 1 giờ, tàu chuyển sang hướng Đông Nam rồi giữ nguyên vận tốc và đi tiếp.
a) Hãy vẽ sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát (1km trên thực tế ứng với 1cm trên bản vẽ).
b) Hãy đo trực tiếp trên bản vẽ và cho biết sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng Vân Phong bao nhiêu kilômét (số đo gần đúng).
c) Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì có thể dùng Định lí Pythagore (Pi – ta – go) để tính chính xác các số đo trong câu b hay không?
Lời giải chi tiết:
a) Xác định các hướng bắc (B), nam (N), đông (Đ), tây (T) như trên hình vẽ.
Giả sử điểm O trên hình là vị trí cảng Vân Phong hay chính là vị trí tàu bắt đầu xuất phát.
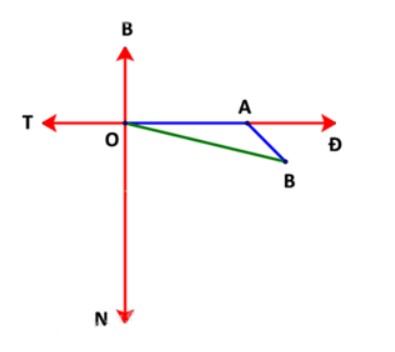
Vận tốc của tàu biển là 20 km/h. Cho nên:
Trong 1 giờ, tàu di chuyển từ điểm xuất phát O theo hướng đông đi đến A với quãng đường OA là S1 = 20 . 1 = 20 (km) tương ứng với 20 cm trên sơ đồ.
Trong 0,5 giờ tiếp theo, tàu di chuyển từ A theo hướng đông nam (hướng tạo với hướng đông một góc 45° về phía nam) đến B với quãng đường AB là S2 = 20 . 0,5 = 10 (km) tương ứng với 10 cm trên sơ đồ.
Vậy ta vẽ được sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát như hình vẽ trên.
b) Trên sơ đồ, ta đo được khoảng cách từ cảng đến tàu là đoạn OB dài khoảng 28 cm.
Do đó, khoảng cách từ cảng đến tàu thực tế khoảng 28 km.
c) Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì sơ đồ đường đi của tàu như sau:
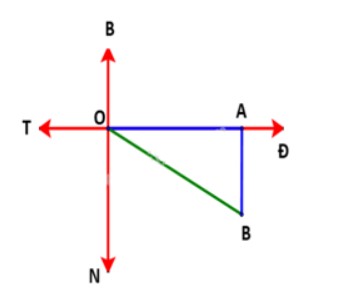
Trong 2 giờ, tàu di chuyển từ điểm xuất phát O theo hướng đông đi đến A với quãng đường OA là 20 . 2 = 40 (km) tương ứng với 40 cm trên sơ đồ.
Sau đó tàu di chuyển từ A theo hướng nam tới vị trí điểm B. Ta có thể tính được quãng đường AB khi biết thời gian di chuyển.
Ta có: AB ⊥ OA nên tam giác OAB vuông tại A.
Khi đó áp dụng định lí Pythagore ta có thể tính được chính xác OB với OB =
√(OA² + AB²) = √(1600 + AB²), do đó ta có thể xác định được chính xác khoảng cách từ điểm B nơi tàu đến tới cảng Vân Phong.
HĐ2 trang 38 Toán 10 Tập 1:
Trong Hình 3.8, hãy thực hiện các bước sau để thiết lập công thức tính a theo b, c và giá trị lượng giác của góc A.
a) Tính a² theo BD2 và CD2.
b) Tính a² theo b, c và DA.
c) Tính DA theo c và cosA.
d) Chứng minh a² = b² + c² – 2bc.cosA.
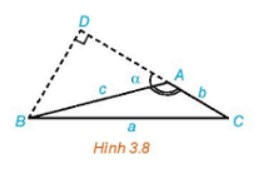
Lời giải chi tiết:
a) Xét ΔBDC vuông tại D, có:
BC² = BD² + DC² (Định lí Pythagore)
Hay a² = BD² + DC²
b) Xét ΔBDA vuông tại D, có:
BA² = BD² + DA² (Định lí Pythagore)
Hay BD² = c² – DA²
Ta lại có: DC = DA + AC = DA + b
Khi đó: a² = c² – DA² + (DA + b)² = c² – DA² + DA² + 2.DA.b + b² = c² + b² + 2.DA.b.
Vậy a² = BD² + DC² = c² + b² + 2.DA.b (1)
c) Xét ΔBDA vuông tại D, có:
DA = AB.cosα = c.cosα.
Lại có:
∠BAC + ∠BAD = 180° (hai góc kề bù)
Hay
∠BAC + α = 180°
⇒α = 180° − ∠BAC
Suy ra cosα = cos∠(180° − ∠BAC) = – cos∠BAC = – cosA.
Do đó, DA = – c.cosA.
d) Thay DA = – c.cosA vào biểu thức (1), ta được:
a² = c² + b2l² – 2bc.cosA
Vậy a² = b² + c² – 2bc cosA. (đpcm)
Câu hỏi trang 38 Toán 10 Tập 1:
Định lý Pythagore có phải là một trường hợp đặc biệt của định lý côsin hay không?
Lời giải chi tiết:
Xét tam giác ABC vuông tại A, ta có:
BC2 = AB2 + AC2 – 2AB.AC.cosA (định lí cos)
= AB2 + AC2 – 2AB.AC.cos900
= AB2 + AC2 (định lí Py – ta – go)
Định lý Pythagore là một trường hợp đặc biệt của định lý côsin.
Khám phá trang 39 Toán 10 Tập 1:
Từ định lý côsin hãy viết các công thức tính cosA, cosB, cosC theo độ dài các cạnh a, b, c của tam giác ABC.
Lời giải chi tiết:
Từ định lý cosin, ta có công thức tính cosA, cosB, cosC theo độ dài các cạnh a, b, c của tam giác ABC là:
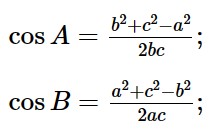
![]()
Luyện tập 1 trang 39 Toán 10 Tập 1:
Cho tam giác ABC, có AB = 5, AC = 8 và ∠A = 45°. Tính độ dài các cạnh và độ lớn các góc còn lại của tam giác.
Lời giải chi tiết:
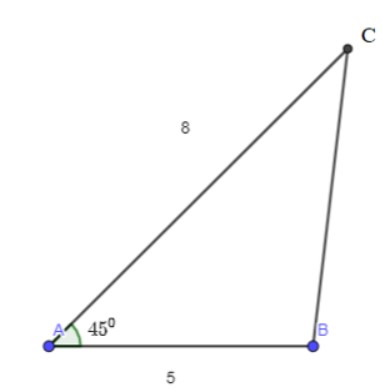
Xét tam giác ABC:
Theo định lí côsin, ta có:
BC² = AB² + AC² – 2.AB.AC.cos A
BC² = 5² + 8² – 2.5.8.cos45°
BC² = 89 − 40√2
BC ≈ 5,7 cm.
Ta có:
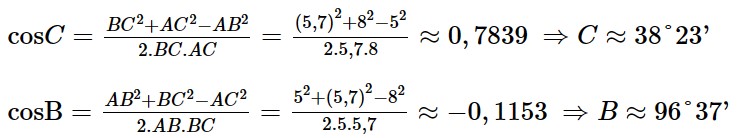
Trải nghiệm trang 39 Toán 10 Tập 1:
Vẽ một tam giác ABC, sau đó đo độ dài các cạnh, số đo góc A và kiểm tra tính đúng đắn của Định lí Côsin tại đỉnh A đối với tam giác đó.
Lời giải chi tiết:
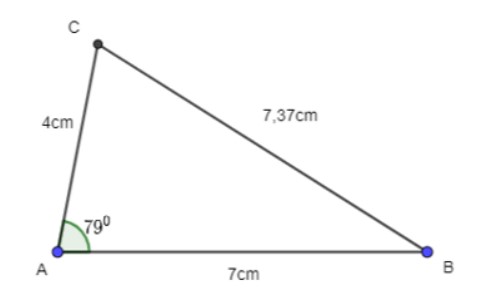
Tiến hành đo các cạnh của tam giác và góc A, ta được:
AB = 7cm, AC = 4cm, BC = 7,37cm và ∠A = 79°.
Khi đó, ta có:
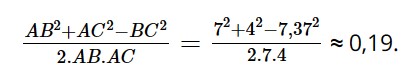
cosA = cos79⁰ ≈ 0,19.
Do đó
cosA = (AB² + AC² − BC²)/2.AB.AC.
Vì vậy Định lý côsin là đúng.
Vận dụng 1 trang 39 Toán 10 Tập 1:
Dùng định lí Côsin, tính khoảng cách được đề cập trong HĐ1b.
Lời giải chi tiết:

Vị trí O là vị trí là vị trí cảng Vân Phong.
Sau khi đi 1 giờ theo hướng đông với vận tốc 20km/h thì tàu đi đến vị trí A, quãng đường OA là: 20.1 = 20 (km)
Đi tiếp 0,5 giờ còn lại theo hướng đông nam cũng với vận tốc 20km/h thì tàu đến vị trí B, quãng đường AB là: 20.0,5 = 10 (km)
Vì hướng đông và hướng đông nam tạo với nhau một góc 450 nên ∠OAB = 135°.
Xét ΔABC, có:
Theo Định lí Côsin, ta có:
OB² = OA² + AB² – 2.OA.AB.cosA
= 20² + 10² – 2.20.10.cos135⁰
= 500 + 200√2
OB ≈ 27,98 km
Vậy sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng vân phong 27,98 km.
3. Định lí Sin:
HĐ3 trang 39 Toán 10 Tập 1:
Trong mỗi hình dưới đây, hãy tính R theo a và sin A.
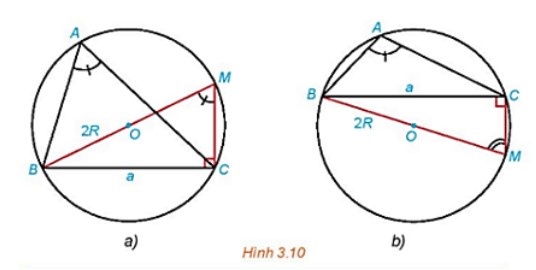
Lời giải chi tiết:
Hình 3.10a):
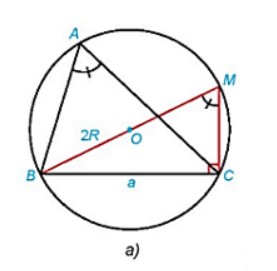
Xét ΔBCM vuông tại C, có:
sin∠BMC = BC/BM = a/2R
Mà ∠BMC + ∠A = 180° (tứ giác ABMC nối tiếp đường tròn (O)).
⇒ ∠A = 180° − ∠BMC
⇒ sin A = sin (180° − ∠BMC) = sin∠BMC = a/2R
⇒ R = a/2sinA.
Hình 3.10b):
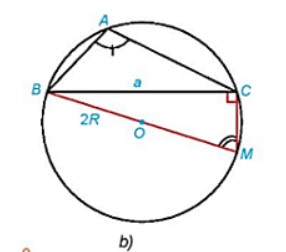
Xét ΔBCM vuông tại C, có:
sin ∠BMC = BC/BM = a/2R
Mà ∠BMC + ∠A = 1/2sđBAC + 1/2sđBMC = ½ . 360⁰ = 180⁰
⇒∠BMC = 180⁰ − ∠A
⇒sin A = sin (180° − ∠BMC) = sin∠BMC = a/2R
⇒R = a/2sinA.
Luyện tập 2 trang 40 Toán 10 Tập 1:
Cho tam giác ABC có b = 8, c = 5 và ∠B = 80⁰. Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài các cạnh còn lại của tam giác
Lời giải chi tiết:
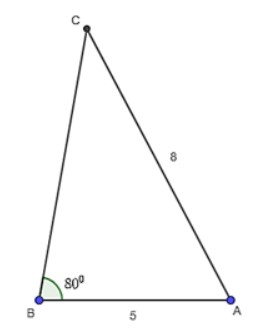
Xét ΔABC, có:
Theo định lý sin, ta có:

4. Giải tam giác và ứng dụng thực tế:
Luyện tập 3 trang 40 Toán 10 Tập 1:
Giải tam giác ABC, biết b = 32, c = 45, ∠A = 87⁰.
Lời giải chi tiết:
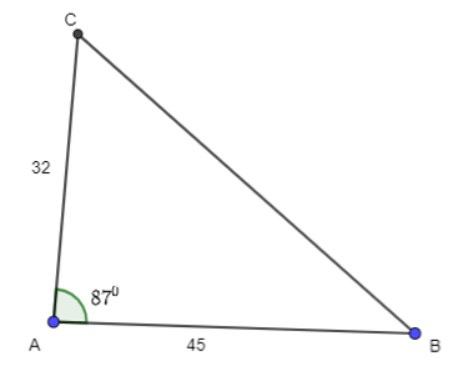
Xét ΔABC, có:
Theo định lý Cos, ta có:
BC² = AB² + AC² – 2.AB.AC.cosA
= 32² + 45² – 2.32.45.cos870 ≈ 2898,27
BC ≈ 53,84
Theo định lí Sin, ta có:

Vận dụng 2 trang 40 Toán 10 Tập 1:
Từ một khu vực có thể quan sát hai đỉnh núi, ta có thể ngắm và đo để xác định khoảng cách giữa hai đỉnh núi đó. Hãy thảo luận để đưa ra các bước cho một cách đo.
Lời giải chi tiết:
– Bước 1: Tại khu vực quan sát, đặt một cọc tiêu cố định tại vị trí A. Kí hiệu hai đỉnh núi lần lượt là điểm B và điểm C.
Đứng tại A, ngắm điểm B và điểm C để đo góc tạo bởi hai hướng ngắm đó (góc BAC).
– Bước 2: Đo khoảng cách từ vị trí ngắm đến từng đỉnh núi, tức là tính AB, AC.
* Tính AB bằng cách:
+ Đứng tại A, ngắm đỉnh núi B để xác định góc ngắm so với mặt đất, kí hiệu là góc α.
+ Theo hướng ngắm, đặt tiếp cọc tiêu tại D gần đỉnh núi hơn và đo đoạn AD. Xác định góc ngắm tại điểm D, kí hiệu là góc β.
Ta có hình vẽ:

– Bước 3: Tính khoảng cách giữa hai đỉnh núi, bằng cách áp dụng định lí côsin cho tam giác ABC để tính độ dài cạnh BC.
Ta có: BC2 = AB2 + AC2 – 2AB.AC.cosBAC.
Với AB, AC, góc BAC đã biết ở các bước trên, thay vào ta tính được BC chính là khoảng cách giữa hai đỉnh núi.
5. Công thức tính diện tích tam giác:
HĐ4 trang 41 Toán 10 Tập 1:
Cho ΔABC với I là tâm đường tròn nội tiếp tam giác.
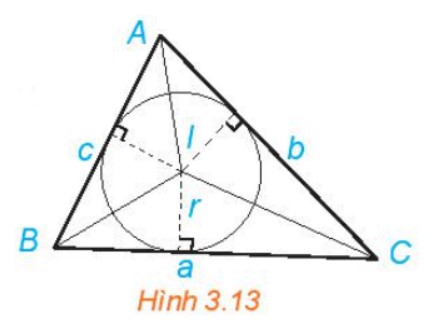
a) Nêu mối liên hệ giữa diện tích tam giác ABC và diện tích tam giác IBC, ICA, IAB.
b) Tính diện tích tam giác ABC theo r, a, b, c.
Lời giải chi tiết:
a) Ta có diện tích tam giác ABC bằng tổng diện tích tam giác IAB, IAC, IBC: S∆ABC = S∆IBC + S∆ICA + S∆IAB
b) Ta có:
SΔIBC = 1/2a.r
SΔICA = 1/2b.r
SΔIAB = 1/2c.r
⇒ SΔABC = SΔIBC + SΔICA + SΔIAB
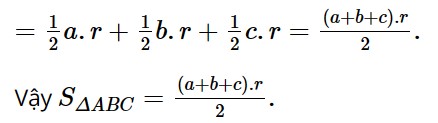
HĐ5 trang 41 Toán 10 Tập 1:
Cho tam giác ABC với đường cao BD
a) Biểu thị BD theo AB và sin A.
b) Viết công thức tính diện tích S của tam giác ABC theo b, c, sin A.
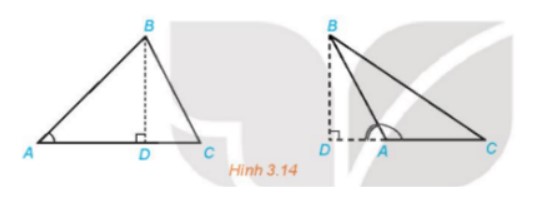
Lời giải chi tiết:
a)
TH1: Đường cao BD nằm trong tam giác ABC
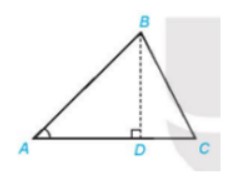
Xét ΔABD vuông tại D, có:
BD = sinA.AB
TH2: Đường cao BD nằm ngoài tam giác ABC
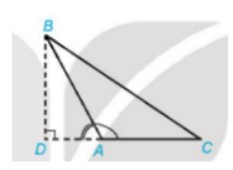
Xét ΔABD vuông tại D, có:
BD = sin∠BAD . AB
Mà ∠BAD + ∠BAC = 180⁰
⇒sin∠BAC = sin(180⁰ − ∠BAD)= sin∠BAD
⇒BD = sin∠BAC . ABb= sinA . AB
Vậy trong cả hai trường hợp ta đều có BD = sinA.AB.
b) TH1. Đường cao BD nằm trong tam giác ABC:

SΔABC = 1/2AC.BD =1/2AC.AB.sinA = 1/2.b.c.sinA.
TH2. Đường cao BD nằm ngoài tam giác ABC:

SΔABC = 1/2AC.BD = 1/2AC.AB.sinA = 1/2.b.c.sinA.
Vậy cả hai trường hợp SΔABC = 1/2.b.c.sinA.
Luyện tập 4 trang 41 Toán 10 Tập 1:
Tính diện tích tam giác ABC có b = 2, ∠B = 30⁰, ∠C = 45⁰.
Lời giải chi tiết:
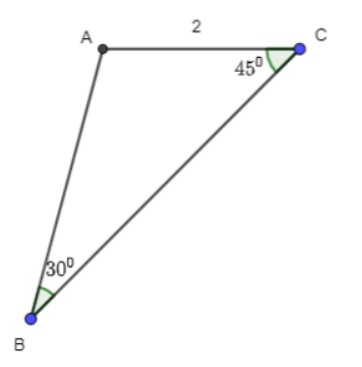

Thảo luận trang 41 Toán 10 Tập 1:
Ta đã biết tính cosA theo độ dài các cạnh của tam giác ABC. Liệu sinA và diện tích S có tính được theo độ dài cạnh của tam giác ABC không?
Lời giải chi tiết:

Vận dụng 3 trang 42 Toán 10 Tập 1:
Công viên Hòa Bình (Hà Nội) có dạng hình ngũ giác ABCDE như Hình 3.17. Dùng chế độ tính khoảng cách giữa hai điểm của Google Maps, một người xác định được các khoảng cách như trong hình vẽ. Theo số liệu đó, em hãy tính diện tích của công viên Hòa Bình.
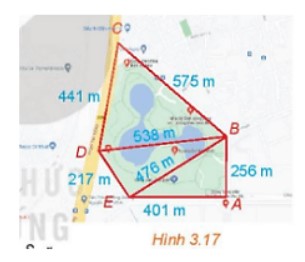
Lời giải chi tiết:


6. Giải bài tập kèm lời giải chi tiết:
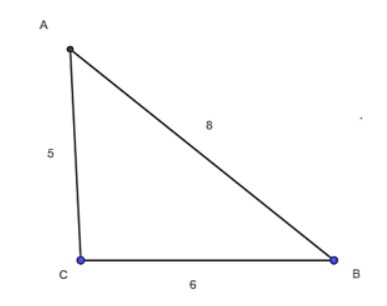
Bài 3.5 trang 42 Toán 10 Tập 1:
Cho tam giác ABC có a = 6, b = 5, c = 8. Tính cosA, S, r.
Lời giải chi tiết:

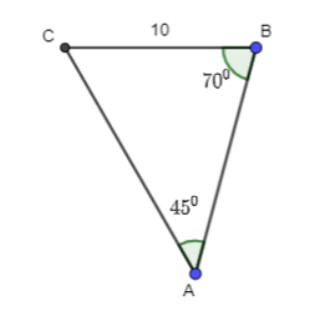
Bài 3.6 trang 42 Toán 10 Tập 1:
Cho tam giác ABC có a = 10, ∠A = 45⁰, ∠B = 70⁰. Tính R, b, c.
Lời giải chi tiết:

Bài 3.7 trang 42 Toán 10 Tập 1:
Giải tam giác ABC và tính diện tích tam giác đó, biết ∠A = 15⁰, ∠B = 130⁰, c = 6.
Lời giải chi tiết:

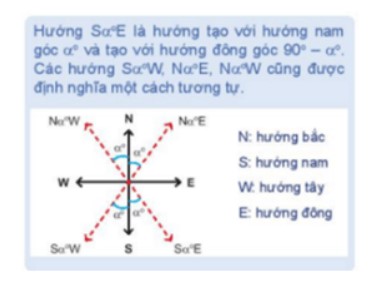
Bài 3.8 trang 42 Toán 10 Tập 1:
Một tàu đánh cá xuất phát từ cảng A, đi theo hướng S70°E với vận tốc 70 km/h. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam với vận tốc 8km/h. Sau 2 giờ kể từ khi động cơ bị hỏng, tàu neo đậu được vào một hòn đảo.
a) Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu.
b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.
Lời giải chi tiết:
Ta có sơ đồ di chuyển của tàu như sau:
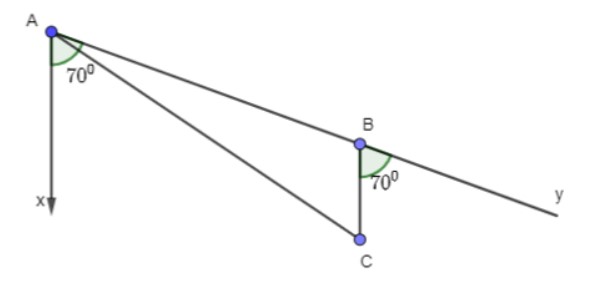
a) Tàu cá xuất phát từ A đi theo hướng S700E với vận tốc 70km/h trong 90 phút = 1,5 giờ thì tàu cá đi được đến B (vị trí tàu bị hỏng), quãng đường AB là: 70.1,5 = 105 (km).
Từ vị trí B tàu cá trôi tự do với vận tốc 8km/h theo hướng nam sau 2h thì neo đậu vào đảo C, khi đó quãng đường BC là: 8.2 = 16km.
Khoảng cách từ cảng A đến nơi tàu neo đậu chính là đoạn AC.
Do tàu đi theo hướng S70⁰E nên phương AB hợp với phương nam Ax một góc 70⁰ nên ∠xAB = 70⁰.
Mà phương BC song song với phương nam Ax nên ∠CBy = ∠xAB = 70⁰
(hai góc đồng vị)
⇒ ∠ABC = 110⁰ (Kề bù ∠CBy)
Xét ΔABC, có:
AC² = AB² + AC² – 2AB.AC.cosB (định lí côsin)
= 105² + 16² – 2.105.16.cos110⁰
≈ 12 430,19
⇒ AC ≈ 111,49 km.
Vậy khoảng cách từ cảng A đến đảo nơi tàu neo đậu khoảng 111,49 km.
b) Xét ΔABC, có:
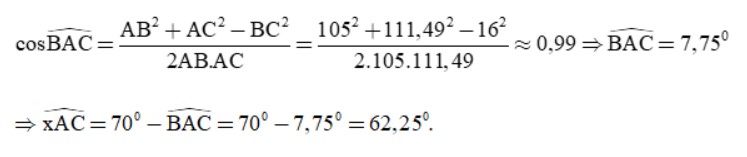
Vậy hướng từ cảng A đến đảo nơi tàu neo đậu là S62,250E.
Bài 3.9 trang 43 Toán 10 Tập 1:
Trên nóc một tòa nhà có một cột ăng – ten cao 5m, Từ một vị trí quan sát A cao 7m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng – ten, với các góc tương ứng là 500 và 400 so với phương nằm ngang (H.3.18).
a) Tính các góc của tam giác ABC.
b) Tính chiều cao của tòa nhà.
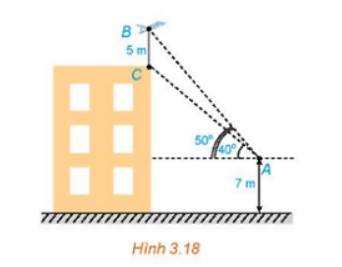
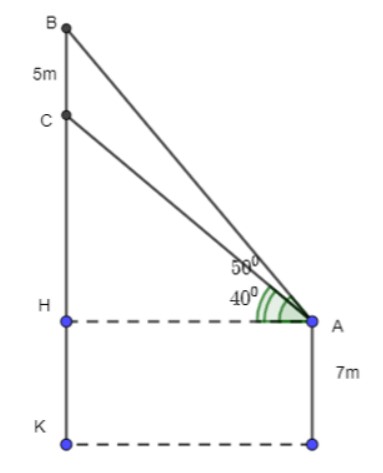
Lời giải chi tiết:
Ta có hình vẽ sau:

Bài 3.10 trang 43 Toán 10 Tập 1:
Từ bãi biển Vũng Chùa, Quảng Bình ta có thể ngắm được Đảo yến. Hãy đề xuất cách xác định bề rộng của hòn đảo (theo chiều ta ngắm được).
Lời giải chi tiết:
– Bước 1. Trên bờ, đặt một cọc ở vị trí A, một cọc ở vị trí B, một cọc ở vị trí C. Đo khoảng cách AB, AC.
– Bước 2. Đứng tại A ngắm điểm B và điểm E để đo góc tạo bởi hai hướng ngắm đó là góc ∠BAE. Đứng tại B ngắm điểm E và điểm A để đo góc tạo bởi hai hướng ngắm đó là góc ∠EBA.
– Bước 3. Dựa vào định lí sin trong tam giác ABE ta tính được cạnh AE.
– Bước 4. Đứng tại A ngắm điểm C và điểm D để đo góc tạo bởi hai hướng ngắm đó là góc ∠DAC. Đứng tại C ngắm điểm D và điểm A để đo góc tạo bởi hai hướng ngắm đó là góc ∠DCA.
– Bước 5. Dựa vào định lí sin trong tam giác ADC tính được AD.
– Bước 6. Xét tam giác ADE, sử dụng định lí cos để tính cạnh DE.
Vậy độ dài DE chính là chiều rộng của đảo.
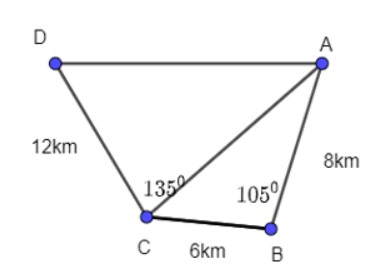
Bài 3.11 trang 43 Toán 10 Tập 1:
Để tránh núi, đường giao thông hiện tại phải đi vòng như mô hình trong Hình 3.19. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ A tới D. Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ.
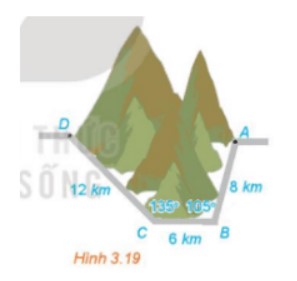
Lời giải chi tiết:
Ta có hình vẽ sau:

THAM KHẢO THÊM:





